Poincaré Duality Spaces
(→Introduction) |
(→Introduction) |
||
| Line 13: | Line 13: | ||
are isomorphisms. | are isomorphisms. | ||
| − | is an isomorphism. Here, $\mathcal B$ is allowed to range over all local coefficient bundles on $X$ | + | is an isomorphism. Here, $\mathcal B$ is allowed to range over all local coefficient bundles on $X$, |
| − | + | but in fact it is sufficient to check the condition when $\mathcal{B}$ is local coefficient bundle over $X$ defined by | |
| − | + | ||
$\Bbb Z[\pi]$, with $\pi$ the fundamental groupoid of $X$. | $\Bbb Z[\pi]$, with $\pi$ the fundamental groupoid of $X$. | ||
Revision as of 18:12, 23 March 2011
|
The user responsible for this page is Klein. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
1 Definition
A Poincaré pair of dimension  consists of a pair of finitely dominated spaces
consists of a pair of finitely dominated spaces 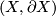 such that there exists a pair
such that there exists a pair ![(\mathcal{L},[X])](/images/math/4/d/8/4d87ca31667018fe8fdd90aa0ebe44db.png) in which
in which 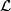 is a bundle of local coefficients on
is a bundle of local coefficients on  which is free abelian of rank one and
which is free abelian of rank one and ![[X] \in H_d(X,\partial X;\mathcal {L})](/images/math/7/7/6/7768eef595bd9088a04de6870c8488d0.png) are such that
are such that
![\displaystyle \cap [X] : H^*(X;\mathcal{B}) \to H_{d-*}(X,\partial X;\mathcal{B} \otimes \mathcal{L})](/images/math/5/0/3/503ba21954ed033ab528e17a746c8962.png)
and
![\displaystyle \cap [X] : H^*(X,\partial X;\mathcal{B}) \to H_{d-*}(X;\mathcal{B} \otimes \mathcal{L})](/images/math/0/3/5/035b25de612189e48ccd1d1f8779bbfc.png)
are isomorphisms.
is an isomorphism. Here, 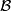 is allowed to range over all local coefficient bundles on
is allowed to range over all local coefficient bundles on  ,
but in fact it is sufficient to check the condition when
,
but in fact it is sufficient to check the condition when 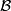 is local coefficient bundle over
is local coefficient bundle over  defined by
defined by
![\Bbb Z[\pi]](/images/math/2/c/8/2c87a27bd90cabf864a1f41ba861b20e.png) , with
, with  the fundamental groupoid of
the fundamental groupoid of  .
.
2 Notes
- If
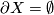 , one says that
, one says that  is a Poincaré duality space. (In view of this, perhaps better terminology would be to call
is a Poincaré duality space. (In view of this, perhaps better terminology would be to call 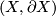 a Poincaré space with boundary.)
a Poincaré space with boundary.)
-
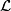 is called an orientation sheaf and
is called an orientation sheaf and ![[X]](/images/math/b/6/9/b697f334e90f4eaaec7edab7dc1a384c.png) is called a fundamental class. The pair
is called a fundamental class. The pair ![(\mathcal L,[X])](/images/math/1/7/7/1771007e5b1c4d7022c004483f8e04e6.png) is unique up to unique isomorphism.
is unique up to unique isomorphism.
- If
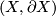 with respect to
with respect to ![(\mathcal{L},[X])](/images/math/4/d/8/4d87ca31667018fe8fdd90aa0ebe44db.png) a Poincar\'e pair of dimension
a Poincar\'e pair of dimension  , then
, then 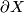 is a Poincaré space of dimension
is a Poincaré space of dimension 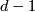 with respect to
with respect to ![(\mathcal {L}_{|\partial X},\partial [X])](/images/math/9/e/8/9e8d4ece0d01ff5da9bfe301be69f15d.png) , where
, where 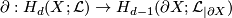 is the boundary homomorphism.
is the boundary homomorphism.
3 Example
A compact (smooth, PL, TOP or homology) manifold 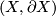 of dimension
of dimension  is a Poincaré duality pair of dimension
is a Poincaré duality pair of dimension  , where
, where 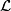 is the orientation sheaf of
is the orientation sheaf of  and
and ![[X]](/images/math/b/6/9/b697f334e90f4eaaec7edab7dc1a384c.png) is the manifold fundamental class.
is the manifold fundamental class.