Poincaré Duality Spaces
From Manifold Atlas
(Difference between revisions)
(→Introduction) |
m |
||
| (12 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
{{Authors|Klein}}{{Stub}} | {{Authors|Klein}}{{Stub}} | ||
| − | ==Introduction== | + | == Introduction == |
<wikitex>; | <wikitex>; | ||
| − | + | </wikitex> | |
==Definition== | ==Definition== | ||
| + | <wikitex>; | ||
| + | A ''Poincaré pair'' of dimension $d$ consists of a finitely dominated CW pair $(X,\partial X)$ for which there exists $$(\mathcal{L},[X])$$ in which | ||
| + | *$\mathcal{L}$ is a bundle of local coefficients on $X$ which is free abelian of rank one, and | ||
| − | + | * $[X] \in H_d(X,\partial X;\mathcal {L})$ is a class such that | |
$$ \cap [X] : H^*(X;\mathcal{B}) \to H_{d-*}(X,\partial X;\mathcal{B} \otimes \mathcal{L})$$ | $$ \cap [X] : H^*(X;\mathcal{B}) \to H_{d-*}(X,\partial X;\mathcal{B} \otimes \mathcal{L})$$ | ||
| Line 13: | Line 16: | ||
are isomorphisms. | are isomorphisms. | ||
| − | + | Here, $\mathcal B$ is allowed to range over all local coefficient bundles on $X$, | |
| − | + | but in fact it is sufficient to check the condition when $\mathcal{B}$ is the local coefficient bundle over $X$ | |
| − | + | associated with $\Bbb Z[\pi]$, where $\pi$ is the fundamental groupoid of $X$. | |
| − | condition when $\mathcal{B}$ is local coefficient bundle over $X$ | + | </wikitex> |
| − | $\Bbb Z[\pi]$, | + | |
| − | + | ||
==Notes== | ==Notes== | ||
| + | <wikitex>; | ||
| + | * If $\partial X = \emptyset$, one says that $X$ is a ''Poincaré duality space.'' (In view of this, perhaps better terminology would be to call $(X,\partial X)$ a ''Poincaré duality space with boundary.'') | ||
| − | * | + | * $\mathcal L$ is called an ''orientation sheaf'' and $[X]$ is called a ''fundamental class.'' The pair $(\mathcal L,[X])$ is unique up to unique isomorphism. |
| − | + | * If $(X,\partial X)$ with respect to $(\mathcal{L},[X])$ a Poincar\'e pair of dimension $d$, then $\partial X$ is a Poincaré space of dimension $d-1$ with respect to $(\mathcal {L}_{|\partial X},\partial [X])$, where $\partial: H_d(X;\mathcal{L}) \to H_{d-1}(\partial X;\mathcal{L}_{|\partial X})$ is the boundary homomorphism. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | * If $(X,\partial X)$ with respect to $(\mathcal{L},[X])$ a Poincar\'e pair of dimension $d$, then $\partial X$ is | + | |
| + | * A finite CW complex $X$ admits the structure of a Poincaré duality space of dimension $n$ if and only if there exists a framed compact smooth manifold $M$ of dimension $m \ge n+3$ such $M$ is homotopy equivalent to $X$ and the inclusion $\partial M \subset M$ has homotopy fiber homotopy equivalent to $S^{m-n-1}$. | ||
| + | </wikitex> | ||
==Example== | ==Example== | ||
| − | + | <wikitex>; | |
| − | A compact (smooth, PL, TOP or homology) manifold $X$ of dimension $d$ is a Poincaré duality | + | A compact (smooth, PL, TOP or homology) manifold $(X,\partial X)$ of dimension $d$ is a Poincaré duality pair of dimension $d$, where $\mathcal L$ is the orientation sheaf of $X$ and $[X]$ is the manifold fundamental class. |
| − | and $[X]$ is the manifold fundamental class. | + | |
| − | + | ||
| − | + | ||
</wikitex> | </wikitex> | ||
Latest revision as of 17:01, 12 June 2013
|
The user responsible for this page is Klein. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
2 Definition
 consists of a finitely dominated CW pair
consists of a finitely dominated CW pair 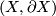 for which there exists
for which there exists ![\displaystyle (\mathcal{L},[X])](/images/math/5/2/4/524f4fda4a49a96a3a03636971fc3aec.png)
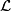 is a bundle of local coefficients on
is a bundle of local coefficients on  which is free abelian of rank one, and
which is free abelian of rank one, and
-
![[X] \in H_d(X,\partial X;\mathcal {L})](/images/math/7/7/6/7768eef595bd9088a04de6870c8488d0.png) is a class such that
is a class such that
![\displaystyle \cap [X] : H^*(X;\mathcal{B}) \to H_{d-*}(X,\partial X;\mathcal{B} \otimes \mathcal{L})](/images/math/5/0/3/503ba21954ed033ab528e17a746c8962.png)
and
![\displaystyle \cap [X] : H^*(X,\partial X;\mathcal{B}) \to H_{d-*}(X;\mathcal{B} \otimes \mathcal{L})](/images/math/0/3/5/035b25de612189e48ccd1d1f8779bbfc.png)
are isomorphisms.
Here, 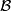 is allowed to range over all local coefficient bundles on
is allowed to range over all local coefficient bundles on  ,
but in fact it is sufficient to check the condition when
,
but in fact it is sufficient to check the condition when 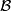 is the local coefficient bundle over
is the local coefficient bundle over  associated with
associated with ![\Bbb Z[\pi]](/images/math/2/c/8/2c87a27bd90cabf864a1f41ba861b20e.png) , where
, where  is the fundamental groupoid of
is the fundamental groupoid of  .
.
3 Notes
- If
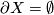 , one says that
, one says that  is a Poincaré duality space. (In view of this, perhaps better terminology would be to call
is a Poincaré duality space. (In view of this, perhaps better terminology would be to call 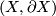 a Poincaré duality space with boundary.)
a Poincaré duality space with boundary.)
-
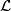 is called an orientation sheaf and
is called an orientation sheaf and ![[X]](/images/math/b/6/9/b697f334e90f4eaaec7edab7dc1a384c.png) is called a fundamental class. The pair
is called a fundamental class. The pair ![(\mathcal L,[X])](/images/math/1/7/7/1771007e5b1c4d7022c004483f8e04e6.png) is unique up to unique isomorphism.
is unique up to unique isomorphism.
- If
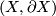 with respect to
with respect to ![(\mathcal{L},[X])](/images/math/4/d/8/4d87ca31667018fe8fdd90aa0ebe44db.png) a Poincar\'e pair of dimension
a Poincar\'e pair of dimension  , then
, then 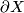 is a Poincaré space of dimension
is a Poincaré space of dimension 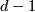 with respect to
with respect to ![(\mathcal {L}_{|\partial X},\partial [X])](/images/math/9/e/8/9e8d4ece0d01ff5da9bfe301be69f15d.png) , where
, where 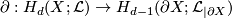 is the boundary homomorphism.
is the boundary homomorphism.
- A finite CW complex
 admits the structure of a Poincaré duality space of dimension
admits the structure of a Poincaré duality space of dimension  if and only if there exists a framed compact smooth manifold
if and only if there exists a framed compact smooth manifold  of dimension
of dimension 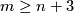 such
such  is homotopy equivalent to
is homotopy equivalent to  and the inclusion
and the inclusion 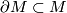 has homotopy fiber homotopy equivalent to
has homotopy fiber homotopy equivalent to 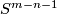 .
.
4 Example
A compact (smooth, PL, TOP or homology) manifold 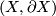 of dimension
of dimension  is a Poincaré duality pair of dimension
is a Poincaré duality pair of dimension  , where
, where 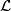 is the orientation sheaf of
is the orientation sheaf of  and
and ![[X]](/images/math/b/6/9/b697f334e90f4eaaec7edab7dc1a384c.png) is the manifold fundamental class.
is the manifold fundamental class.