Oriented cover
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
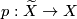 be a regular covering of a connected space with orientation character
be a regular covering of a connected space with orientation character 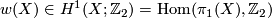 . Let
. Let  denote the group of covering translations. Since
denote the group of covering translations. Since  is a regular cover
is a regular cover 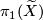 is a normal subgroup of
is a normal subgroup of 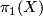 and
and 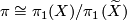 (See [Hatcher2002, Proposition 1.39]). Let
(See [Hatcher2002, Proposition 1.39]). Let 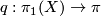 denote the quotient map. The orientation character of the cover factors as
denote the quotient map. The orientation character of the cover factors as 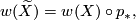
 is orientable if all loops in
is orientable if all loops in  project to orientable loops in
project to orientable loops in  .
.
Lemma 1.1.
The cover  is orientable if and only if the orientation character
is orientable if and only if the orientation character 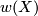 factors through
factors through  .
.
Proof. Consider the diagram
![\displaystyle \xymatrix{ \pi_1(\widetilde{X}) \ar[dr]^-{w(\widetilde{X})} \ar[d] ^-{p_*}& \\ \pi_1(X) \ar[d]^-{q}\ar[r]^{w(X)} & \Zz_2 \\ \pi \ar@{-->}[ur]^-{w} & }](/images/math/b/6/4/b64ea561411c95b6573af97daff2a0cf.png)
If there exists a  such that
such that 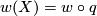 , then
, then 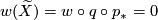 . Conversely if
. Conversely if 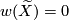 then the map
then the map
![\displaystyle \begin{array}{rcl} w:\pi & \to & \Zz_2 \\ {[\alpha]} & \mapsto & w(X)(\alpha)\end{array}](/images/math/d/5/1/d5172ae95d0e25d03d671e7163b9093a.png)
for any representative 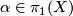 of
of ![[\alpha]\in \pi](/images/math/f/2/d/f2db939a6cc390c32c31277802a708da.png) is well defined and factors
is well defined and factors 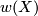 .
.

In light of this we make the following definition.
2 Definition
An orientable cover 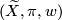 of a (connected) space
of a (connected) space  with an orientation character
with an orientation character 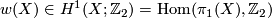 is a regular covering of
is a regular covering of  with group of covering translations
with group of covering translations  , together with an orientation character
, together with an orientation character 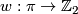 such that
such that
![\displaystyle \xymatrix{ w(X): \pi_1(X) \ar[r] & \pi \ar[r]^-{w} & \Zz_2. }](/images/math/b/e/9/be97428a3e1bede98322d68b277a57c9.png)
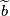 of a basepoint
of a basepoint 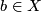 to
to  .
.
3 Lifts correspond to orientations
Let 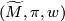 be an oriented cover of a connected manifold
be an oriented cover of a connected manifold 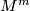 . A choice of lift
. A choice of lift 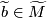 corresponds to a choice of
corresponds to a choice of  -twisted fundamental class
-twisted fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) . Given a lift
. Given a lift 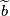 a fundamental class
a fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) is uniquely determined by setting its restriction to
is uniquely determined by setting its restriction to 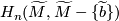 to be
to be 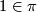 and extending equivariantly. Conversely, given a fundamental class
and extending equivariantly. Conversely, given a fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) define
define 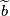 to be the lift such that the restriction of
to be the lift such that the restriction of ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) to
to 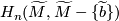 is
is 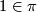 .
.
4 Examples
The two most important examples of oriented covers are the universal cover 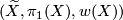 and the orientation double cover
and the orientation double cover 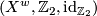 . These correspond to the two extreme cases of factoring the orientation character via
. These correspond to the two extreme cases of factoring the orientation character via 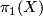 and
and  respectively. Every oriented cover is a regular cover of
respectively. Every oriented cover is a regular cover of 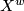 and has
and has  as a regular cover - this is a consequence of the fact that if
as a regular cover - this is a consequence of the fact that if 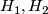 are normal subgroups of
are normal subgroups of  with
with 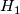 a subgroup of
a subgroup of 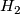 then
then 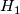 is a normal subgroup of
is a normal subgroup of 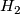 .
.
5 Convention
Tex syntax erroris already orientatable, the orientation double cover
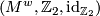 consists of two disjoint copies of
consists of two disjoint copies of Tex syntax error. Any orientation of
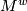 that we choose must involve giving the two copies of
that we choose must involve giving the two copies of Tex syntax erroropposite orientations, otherwise it will not be in the image of the map
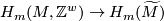 .
.
6 References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001
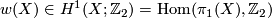 . Let
. Let  denote the group of covering translations. Since
denote the group of covering translations. Since  is a regular cover
is a regular cover 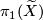 is a normal subgroup of
is a normal subgroup of 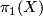 and
and 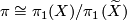 (See [Hatcher2002, Proposition 1.39]). Let
(See [Hatcher2002, Proposition 1.39]). Let 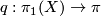 denote the quotient map. The orientation character of the cover factors as
denote the quotient map. The orientation character of the cover factors as 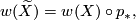
 is orientable if all loops in
is orientable if all loops in  project to orientable loops in
project to orientable loops in  .
.
Lemma 1.1.
The cover  is orientable if and only if the orientation character
is orientable if and only if the orientation character 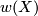 factors through
factors through  .
.
Proof. Consider the diagram
![\displaystyle \xymatrix{ \pi_1(\widetilde{X}) \ar[dr]^-{w(\widetilde{X})} \ar[d] ^-{p_*}& \\ \pi_1(X) \ar[d]^-{q}\ar[r]^{w(X)} & \Zz_2 \\ \pi \ar@{-->}[ur]^-{w} & }](/images/math/b/6/4/b64ea561411c95b6573af97daff2a0cf.png)
If there exists a  such that
such that 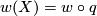 , then
, then 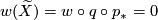 . Conversely if
. Conversely if 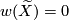 then the map
then the map
![\displaystyle \begin{array}{rcl} w:\pi & \to & \Zz_2 \\ {[\alpha]} & \mapsto & w(X)(\alpha)\end{array}](/images/math/d/5/1/d5172ae95d0e25d03d671e7163b9093a.png)
for any representative 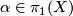 of
of ![[\alpha]\in \pi](/images/math/f/2/d/f2db939a6cc390c32c31277802a708da.png) is well defined and factors
is well defined and factors 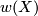 .
.

In light of this we make the following definition.
2 Definition
An orientable cover 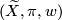 of a (connected) space
of a (connected) space  with an orientation character
with an orientation character 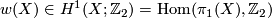 is a regular covering of
is a regular covering of  with group of covering translations
with group of covering translations  , together with an orientation character
, together with an orientation character 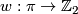 such that
such that
![\displaystyle \xymatrix{ w(X): \pi_1(X) \ar[r] & \pi \ar[r]^-{w} & \Zz_2. }](/images/math/b/e/9/be97428a3e1bede98322d68b277a57c9.png)
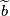 of a basepoint
of a basepoint 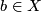 to
to  .
.
3 Lifts correspond to orientations
Let 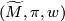 be an oriented cover of a connected manifold
be an oriented cover of a connected manifold 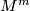 . A choice of lift
. A choice of lift 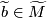 corresponds to a choice of
corresponds to a choice of  -twisted fundamental class
-twisted fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) . Given a lift
. Given a lift 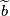 a fundamental class
a fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) is uniquely determined by setting its restriction to
is uniquely determined by setting its restriction to 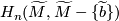 to be
to be  and extending equivariantly. Conversely, given a fundamental class
and extending equivariantly. Conversely, given a fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) define
define  to be the lift such that the restriction of
to be the lift such that the restriction of ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) to
to 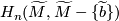 is
is 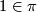 .
.
4 Examples
The two most important examples of oriented covers are the universal cover 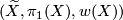 and the orientation double cover
and the orientation double cover 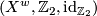 . These correspond to the two extreme cases of factoring the orientation character via
. These correspond to the two extreme cases of factoring the orientation character via 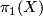 and
and  respectively. Every oriented cover is a regular cover of
respectively. Every oriented cover is a regular cover of 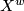 and has
and has  as a regular cover - this is a consequence of the fact that if
as a regular cover - this is a consequence of the fact that if 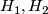 are normal subgroups of
are normal subgroups of  with
with 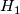 a subgroup of
a subgroup of 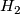 then
then 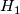 is a normal subgroup of
is a normal subgroup of 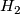 .
.
5 Convention
Tex syntax erroris already orientatable, the orientation double cover
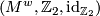 consists of two disjoint copies of
consists of two disjoint copies of Tex syntax error. Any orientation of
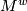 that we choose must involve giving the two copies of
that we choose must involve giving the two copies of Tex syntax erroropposite orientations, otherwise it will not be in the image of the map
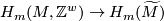 .
.
6 References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001
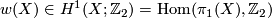 . Let
. Let  denote the group of covering translations. Since
denote the group of covering translations. Since  is a regular cover
is a regular cover 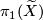 is a normal subgroup of
is a normal subgroup of 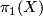 and
and 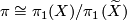 (See [Hatcher2002, Proposition 1.39]). Let
(See [Hatcher2002, Proposition 1.39]). Let 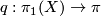 denote the quotient map. The orientation character of the cover factors as
denote the quotient map. The orientation character of the cover factors as 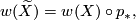
 is orientable if all loops in
is orientable if all loops in  project to orientable loops in
project to orientable loops in  .
.
Lemma 1.1.
The cover  is orientable if and only if the orientation character
is orientable if and only if the orientation character 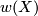 factors through
factors through  .
.
Proof. Consider the diagram
![\displaystyle \xymatrix{ \pi_1(\widetilde{X}) \ar[dr]^-{w(\widetilde{X})} \ar[d] ^-{p_*}& \\ \pi_1(X) \ar[d]^-{q}\ar[r]^{w(X)} & \Zz_2 \\ \pi \ar@{-->}[ur]^-{w} & }](/images/math/b/6/4/b64ea561411c95b6573af97daff2a0cf.png)
If there exists a  such that
such that 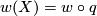 , then
, then 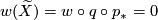 . Conversely if
. Conversely if 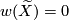 then the map
then the map
![\displaystyle \begin{array}{rcl} w:\pi & \to & \Zz_2 \\ {[\alpha]} & \mapsto & w(X)(\alpha)\end{array}](/images/math/d/5/1/d5172ae95d0e25d03d671e7163b9093a.png)
for any representative 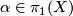 of
of ![[\alpha]\in \pi](/images/math/f/2/d/f2db939a6cc390c32c31277802a708da.png) is well defined and factors
is well defined and factors 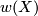 .
.

In light of this we make the following definition.
2 Definition
An orientable cover 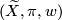 of a (connected) space
of a (connected) space  with an orientation character
with an orientation character 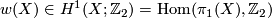 is a regular covering of
is a regular covering of  with group of covering translations
with group of covering translations  , together with an orientation character
, together with an orientation character 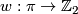 such that
such that
![\displaystyle \xymatrix{ w(X): \pi_1(X) \ar[r] & \pi \ar[r]^-{w} & \Zz_2. }](/images/math/b/e/9/be97428a3e1bede98322d68b277a57c9.png)
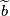 of a basepoint
of a basepoint 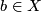 to
to  .
.
3 Lifts correspond to orientations
Let 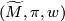 be an oriented cover of a connected manifold
be an oriented cover of a connected manifold 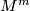 . A choice of lift
. A choice of lift 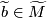 corresponds to a choice of
corresponds to a choice of  -twisted fundamental class
-twisted fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) . Given a lift
. Given a lift 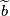 a fundamental class
a fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) is uniquely determined by setting its restriction to
is uniquely determined by setting its restriction to 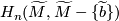 to be
to be 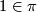 and extending equivariantly. Conversely, given a fundamental class
and extending equivariantly. Conversely, given a fundamental class ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) define
define 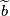 to be the lift such that the restriction of
to be the lift such that the restriction of ![[\widetilde{M}]\in H_m(M,M^w)](/images/math/a/2/c/a2cbdf5848de770843c0b26fdc16dfca.png) to
to 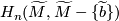 is
is 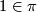 .
.
4 Examples
The two most important examples of oriented covers are the universal cover 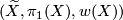 and the orientation double cover
and the orientation double cover 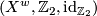 . These correspond to the two extreme cases of factoring the orientation character via
. These correspond to the two extreme cases of factoring the orientation character via 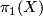 and
and  respectively. Every oriented cover is a regular cover of
respectively. Every oriented cover is a regular cover of 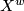 and has
and has  as a regular cover - this is a consequence of the fact that if
as a regular cover - this is a consequence of the fact that if 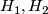 are normal subgroups of
are normal subgroups of  with
with 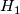 a subgroup of
a subgroup of 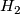 then
then 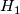 is a normal subgroup of
is a normal subgroup of 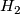 .
.
5 Convention
Tex syntax erroris already orientatable, the orientation double cover
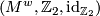 consists of two disjoint copies of
consists of two disjoint copies of Tex syntax error. Any orientation of
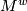 that we choose must involve giving the two copies of
that we choose must involve giving the two copies of Tex syntax erroropposite orientations, otherwise it will not be in the image of the map
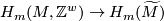 .
.
6 References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001