|
|
| (12 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| − | <!-- COMMENT:
| |
| − |
| |
| − | To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments:
| |
| − |
| |
| − | - For statements like Theorem, Lemma, Definition etc., use e.g.
| |
| − | {{beginthm|Theorem 1|(Milnor)}} ... ... ... {{endthm}}.
| |
| − |
| |
| − | - For references, use e.g. {{cite|Milnor1958b}}.
| |
| − |
| |
| − | END OF COMMENT
| |
| − |
| |
| − | -->
| |
| − | == Question ==
| |
| | <wikitex>; | | <wikitex>; |
| − | Take the stable vector bundle $\xi$ over the $4i$-sphere corresponding to a generator of $\pi_{4i}(BO) = \mathbb{Z}$. By defintion the the primary obstruction to trivialising $\xi^{4i}$ is an obstruction class $x \in H^{4i}(S^{4i})$ which generates $H^{4i}(S^{4i}) \cong \mathbb{Z}$. | + | Take the stable vector bundle $\xi$ over the $4i$-sphere corresponding to a generator of $\pi_{4i}(BO) = \mathbb{Z}$. By defintion, the the primary obstruction to trivialising $\xi^{4i}$ is a cohomology class $x \in H^{4i}(S^{4i}; \pi_{4k-1}(O)) = H^{4i}(S^{4i})$ which generates $H^{4i}(S^{4i}) \cong \mathbb{Z}$. |
| | | | |
| − | {{beginthm|Question}} | + | {{beginthm|Exercise}} |
| − | What is the $i$-th integral Pontryagin class of $\xi^{4i}$, $p_i(\xi) \in H^{4i}(S^{4i})$ ?
| + | Determine the $i$-th integral Pontryagin class of $\xi^{4i}$, $p_i(\xi) \in H^{4i}(S^{4i})$, in terms of $x$. |
| | + | {{endthm}} |
| | </wikitex> | | </wikitex> |
| − | == Answer ==
| + | [[Category:Exercises]] |
| − | <wikitex>;
| + | [[Category:Exercises with solution]] |
| − | Let $a_j = (3 - (-1)^j)/2$, let $k!$ be the integer k-factorial and recall that $x \in H^{4i}(S^{4i})$ is a generator.
| + | |
| − | {{beginthm|Theorem|{{cite|Kervaire1959}}}}
| + | |
| − | There is an identity
| + | |
| − | $$ p_i(\xi^{4i}) = \pm a_i \cdot (2i-1)! \cdot x \in H^{4i}(S^{4i}).$$
| + | |
| − | | + | |
| − | Similarly, if $\eta$ denotes the complex vector bundle over $S^{2i}$ corresponding to a generator of $\pi_{2i}(BU)\cong \mathbb{Z}$, then its Chern class is given by
| + | |
| − | $$ c_i(\eta) = \pm (i-1)! \cdot y\in H^{2i}(S^{2i}),$$
| + | |
| − | where $y\in H^{2i}(S^{2i})\cong \mathbb{Z}$ is a generator.
| + | |
| − | {{endthm|Theorem}}
| + | |
| − | | + | |
| − | A way to prove the Theorem is to use the Chern character
| + | |
| − | $$\tilde K_0(X)\to \tilde H^{ev}(X;\mathbb{Q})$$
| + | |
| − | from complex topological $K$-theory. It can be defined using the explicit formula
| + | |
| − | $$ ch(\xi)= \sum_{k>0} s_k(c_1(\xi),\dots,c_k(\xi))/k! $$
| + | |
| − | for a virtual complex vector bundle $\xi$, where $s_k$ are the Newton polynomials. In the case $X=S^{2n}$ two special things occur:
| + | |
| − | | + | |
| − | #The Chern character is injective with image $H^{2n}(S^{2n};\mathbb{Z})$. (This follows inductively from the case $n=0$ using Bott periodicity.)
| + | |
| − | #A calculation shows that the image of a (virtual) complex vector bundle $\xi$ over $S^{2n}$ is given by $\pm c_n(\xi)/(n-1)!$.
| + | |
| − | | + | |
| − | Hence, $c_i(\eta)$ is given by $\pm (n-1)!$ times a generator. This establishes the second part of the Theorem.
| + | |
| − | | + | |
| − | The first part follows using the definition $p_i(\xi)=c_{2i}(\xi\otimes_\mathbb{R} \mathbb{C})$ together with the fact that complexification induces a map
| + | |
| − | $$ - \otimes_\mathbb{R} \mathbb{C}\colon \widetilde{KO}^0(S^{4i})\to \tilde K^0(S^{4i}) $$
| + | |
| − | which is given by multiplication by $a_i$, i.e. is a isomorphism in degrees $8i$ and multiplication by 2 in degrees $8i+4$.
| + | |
| − | </wikitex>
| + | |
| − | | + | |
| − | == Further discussion ==
| + | |
| − | <wikitex>;
| + | |
| − | ...
| + | |
| − | </wikitex>
| + | |
| − | | + | |
| − | == References ==
| + | |
| − | {{#RefList:}}
| + | |
| − | | + | |
| − | <!-- Please add further headings according to your needs. -->
| + | |
| − | | + | |
| − | [[Category:Questions]] | + | |
| − | [[Category:Study questions]] | + | |
 over the
over the 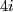 -sphere corresponding to a generator of
-sphere corresponding to a generator of 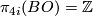 . By defintion, the the primary obstruction to trivialising
. By defintion, the the primary obstruction to trivialising 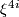 is a cohomology class
is a cohomology class 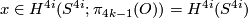 which generates
which generates 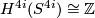 .
.
 -th integral Pontryagin class of
-th integral Pontryagin class of 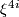 ,
, 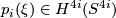 , in terms of
, in terms of  .
.