Obstruction classes and Pontrjagin classes (Ex)
m |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Question == | == Question == | ||
<wikitex>; | <wikitex>; | ||
| Line 34: | Line 22: | ||
from complex topological $K$-theory. It can be defined using the explicit formula | from complex topological $K$-theory. It can be defined using the explicit formula | ||
$$ ch(\xi)= \sum_{k>0} s_k(c_1(\xi),\dots,c_k(\xi))/k! $$ | $$ ch(\xi)= \sum_{k>0} s_k(c_1(\xi),\dots,c_k(\xi))/k! $$ | ||
| − | for a virtual complex vector bundle $\xi$, where $s_k$ are the Newton polynomials. In the case $X=S^{2n}$ two special things occur: | + | for a virtual complex vector bundle $\xi$, where $s_k$ are the [[Newton polynomials]]. In the case $X=S^{2n}$ two special things occur: |
| − | #The Chern character is injective with image $H^{2n}(S^{2n};\mathbb{ | + | #The Chern character is injective with image $H^{2n}(S^{2n};\mathbb{Q})$. This follows from the case $n=1$ using Bott periodicity and multiplicativity: $$ \tilde K_0(S^{2n}) \cong\tilde K_0(S^2)\otimes \dots \otimes\tilde K_0(S^2) \to \tilde H^{ev}(S^{2};\mathbb{Q})\otimes \dots \otimes \tilde H^{ev}(S^{2};\mathbb{Q})\cong \tilde H^{ev}(S^{2n};\mathbb{Q}) $$ |
#A calculation shows that the image of a (virtual) complex vector bundle $\xi$ over $S^{2n}$ is given by: | #A calculation shows that the image of a (virtual) complex vector bundle $\xi$ over $S^{2n}$ is given by: | ||
$$ch(\xi)= s_n(0,\dots, 0, c_n(\xi))/n! = \pm c_n(\xi)/(n-1)!$$ | $$ch(\xi)= s_n(0,\dots, 0, c_n(\xi))/n! = \pm c_n(\xi)/(n-1)!$$ | ||
| Line 42: | Line 30: | ||
Hence, $c_i(\eta)$ is given by $\pm (n-1)!$ times a generator. This establishes the second part of the Theorem. | Hence, $c_i(\eta)$ is given by $\pm (n-1)!$ times a generator. This establishes the second part of the Theorem. | ||
| − | The first part follows using the definition $p_i(\xi)= | + | The first part follows using the definition $p_i(\xi)= (-1)^ic_{2i}(\xi\otimes_\mathbb{R} \mathbb{C})$ together with the fact that complexification induces a map |
$$ - \otimes_\mathbb{R} \mathbb{C}\colon \widetilde{KO}^0(S^{4i})\to \tilde K^0(S^{4i}) $$ | $$ - \otimes_\mathbb{R} \mathbb{C}\colon \widetilde{KO}^0(S^{4i})\to \tilde K^0(S^{4i}) $$ | ||
which is given by multiplication by $a_i$, i.e. is a isomorphism in degrees $8i$ and multiplication by 2 in degrees $8i+4$. | which is given by multiplication by $a_i$, i.e. is a isomorphism in degrees $8i$ and multiplication by 2 in degrees $8i+4$. | ||
Revision as of 13:35, 7 February 2012
Contents |
1 Question
Take the stable vector bundle  over the
over the 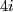 -sphere corresponding to a generator of
-sphere corresponding to a generator of 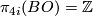 . By defintion the the primary obstruction to trivialising
. By defintion the the primary obstruction to trivialising 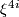 is an obstruction class
is an obstruction class 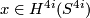 which generates
which generates 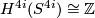 .
.
Question 1.1.
What is the -th integral Pontryagin class of
-th integral Pontryagin class of 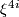 ,
, 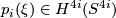 ?
? 2 Answer
Let 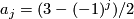 , let
, let 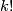 be the integer k-factorial and recall that
be the integer k-factorial and recall that 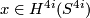 is a generator.
is a generator.
Theorem 2.1 [Kervaire1959]. There is an identity
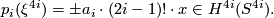
Similarly, if 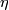 denotes the complex vector bundle over
denotes the complex vector bundle over 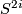 corresponding to a generator of
corresponding to a generator of 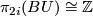 , then its Chern class is given by
, then its Chern class is given by
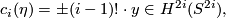
where 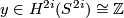 is a generator.
is a generator.
Justification
A way to prove the Theorem 2.1 is to use the Chern character
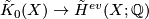
from complex topological  -theory. It can be defined using the explicit formula
-theory. It can be defined using the explicit formula
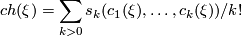
for a virtual complex vector bundle  , where
, where 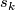 are the Newton polynomials. In the case
are the Newton polynomials. In the case 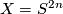 two special things occur:
two special things occur:
- The Chern character is injective with image
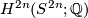 . This follows from the case
. This follows from the case  using Bott periodicity and multiplicativity:
using Bott periodicity and multiplicativity: 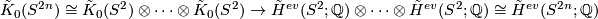
- A calculation shows that the image of a (virtual) complex vector bundle
 over
over 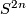 is given by:
is given by:
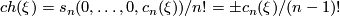
Hence, 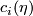 is given by
is given by 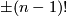 times a generator. This establishes the second part of the Theorem.
times a generator. This establishes the second part of the Theorem.
The first part follows using the definition 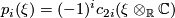 together with the fact that complexification induces a map
together with the fact that complexification induces a map
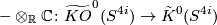
which is given by multiplication by 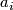 , i.e. is a isomorphism in degrees
, i.e. is a isomorphism in degrees 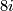 and multiplication by 2 in degrees
and multiplication by 2 in degrees 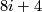 .
.
3 Further discussion
The integrality condition for the Chern character (and the additional factor of 2 for complexifications of real vector bundles in dimensions 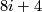 ) also follows from the Atiyah-Singer Index Theorem.
) also follows from the Atiyah-Singer Index Theorem.
4 References
- [Kervaire1959] M. A. Kervaire, A note on obstructions and characteristic classes, Amer. J. Math. 81 (1959), 773–784. MR0107863 (21 #6585) Zbl 0124.16302