Obstruction classes and Pontrjagin classes (Ex)
(Difference between revisions)
(→Question) |
|||
| Line 13: | Line 13: | ||
== Question == | == Question == | ||
<wikitex>; | <wikitex>; | ||
| − | Take the stable vector bundle $\xi$ over the $4i$-sphere corresponding to a generator of $\pi_{4i}(BO) = \mathbb{Z}$. | + | Take the stable vector bundle $\xi$ over the $4i$-sphere corresponding to a generator of $\pi_{4i}(BO) = \mathbb{Z}$. By defintion the the primary obstruction to trivialising $\xi^{4i}$ is an obstruction class $x \in H^{4i}(S^{4i})$ which generates $H^{4i}(S^{4i}) \cong \mathbb{Z}$. |
{{beginthm|Question}} | {{beginthm|Question}} | ||
| − | What is the $i$-th integral Pontryagin class of $\xi^{4i}$, $p_i(\xi) \in H^{4i}(S^{4i}) | + | What is the $i$-th integral Pontryagin class of $\xi^{4i}$, $p_i(\xi) \in H^{4i}(S^{4i})$ ? |
</wikitex> | </wikitex> | ||
| + | |||
== Answer == | == Answer == | ||
<wikitex>; | <wikitex>; | ||
Revision as of 18:15, 17 March 2010
Contents |
1 Question
Take the stable vector bundle  over the
over the 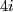 -sphere corresponding to a generator of
-sphere corresponding to a generator of 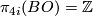 . By defintion the the primary obstruction to trivialising
. By defintion the the primary obstruction to trivialising 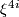 is an obstruction class
is an obstruction class 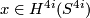 which generates
which generates 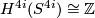 .
.
Question 1.1.
What is the -th integral Pontryagin class of
-th integral Pontryagin class of 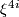 ,
, 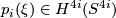 ?
?
2 Answer
Let 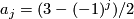 , let
, let 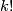 be the integer k-factorial and let
be the integer k-factorial and let 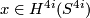 be a generator.
be a generator.
Theorem 2.1 [Kervaire1959]. There is an identity
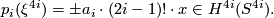
3 Further discussion
...
4 References
- [Kervaire1959] M. A. Kervaire, A note on obstructions and characteristic classes, Amer. J. Math. 81 (1959), 773–784. MR0107863 (21 #6585) Zbl 0124.16302