Novikov Conjecture

Revision as of 17:01, 4 March 2012

1 Introduction

Let ${{Stub}}== Introduction == <wikitex>; Let $M$ be a closed oriented $n$-dimensional smooth manifold with a map $f : M \to B\pi$ for some discrete group $\pi$ and let $\alpha \in H^{n-4*}(B\pi; \Qq)$ be a rational cohomology class. The ''higher signature'' of $M$ defined by $(f, \alpha)$ is the rational number $$ \sigma_\alpha(M, f) = \langle L_M \cup f^*\alpha, [M] \rangle \in \Qq $$ where $L_M \in H^{4*}(M; \Qq)$ is the Hirzebruch L-class of $M$. Let $h: N \to M$ be a homotopy equivalence of closed oriented smooth manifolds. The '''Novikov conjecture''' states $$ \sigma_\alpha(N, f \circ h) = \sigma_\alpha(M, f)$$ for all $\pi$, $f$, $\alpha$ and for all homotopy equivalences $h : N \to M$. For the trivial group $\pi$ the conjecture is true by Hirzebruch's signature theorem. The original 1969 statement of the Novikov conjecture may be found in \cite{Novikov1970} and \cite{Novikov1970a}: a history and survey including the original statement in Russian with a translation into English may be found in \cite{Ferry&Ranicki&Rosenberg1995b}. In the last 40 years the Novikov conjecture and the related conjectures of Borel and Farrell-Jones have been the subject of a great deal of research. In \cite{Novikov2010} Novikov described how he came to formulate the conjecture. More information may be found in \cite{Ferry&Ranicki&Rosenberg1995}, \cite{Ferry&Ranicki&Rosenberg1995a}, \cite{Ranicki1995} and \cite{Davis2000}. </wikitex> == References == {{#RefList:}} == External links == * The Wikipedia page about [[Wikipedia:Novikov_conjecture|the Novikov conjecture]]. 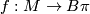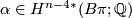[[Category:Theory]] [[Category:Surgery]]M$ be a closed oriented $n$-dimensional smooth manifold with a map $f : M \to B\pi$ for some discrete group $\pi$ and let $\alpha \in H^{n-4*}(B\pi; \Qq)$ be a rational cohomology class. 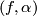The higher signature of $M$ defined by $(f, \alpha)$ is the rational number

$$\displaystyle \sigma_\alpha(M, f) = \langle L_M \cup f^*\alpha, [M] \rangle \in \Qq$$

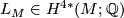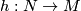where $L_M \in H^{4*}(M; \Qq)$ is the Hirzebruch L-class of $M$. Let $h: N \to M$ be a homotopy equivalence of closed oriented smooth manifolds. The Novikov conjecture states

$$\displaystyle \sigma_\alpha(N, f \circ h) = \sigma_\alpha(M, f)$$

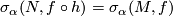
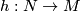for all $\pi$, $f$, $\alpha$ and for all homotopy equivalences $h : N \to M$. For the trivial group $\pi$ the conjecture is true by Hirzebruch's signature theorem.

The original 1969 statement of the Novikov conjecture may be found in [Novikov1970] and [Novikov1970a]: a history and survey including the original statement in Russian with a translation into English may be found in [Ferry&Ranicki&Rosenberg1995b]. In the last 40 years the Novikov conjecture and the related conjectures of Borel and Farrell-Jones have been the subject of a great deal of research. In [Novikov2010] Novikov described how he came to formulate the conjecture.

More information may be found in [Ferry&Ranicki&Rosenberg1995], [Ferry&Ranicki&Rosenberg1995a], [Ranicki1995] and [Davis2000].

2 References

• [Davis2000] J. F. Davis, Manifold aspects of the Novikov conjecture, Surveys on surgery theory, Vol. 1, Princeton Univ. Press (2000), 195–224. MR1747536 (2002a:57037) Zbl 0948.57001
• [Ferry&Ranicki&Rosenberg1995] S. C. Ferry, A. A. Ranicki and J. Rosenberg, Novikov conjectures, index theorems and rigidity. Vol. 1. London Math. Soc. Lecture Note Ser., 226, Cambridge Univ. Press, Cambridge, 1995. MR1388294 (96m:57002) Zbl 0829.00027
• [Ferry&Ranicki&Rosenberg1995a] S. C. Ferry, A. A. Ranicki and J. Rosenberg, Novikov conjectures, index theorems and rigidity. Vol. 2, London Math. Soc. Lecture Note Ser., 227, Cambridge Univ. Press, Cambridge, 1995. MR1388306 (96m:57003) Zbl 0829.00028
• [Ferry&Ranicki&Rosenberg1995b] S. C. Ferry, A. A. Ranicki and J. Rosenburg, A history and survey of the Novikov conjecture in Ferry&Ranicki&Rosenberg1995 7–66, London Math. Soc. Lecture Note Ser., 226, Cambridge Univ. Press, Cambridge, 1995. MR1388295 (97f:57036) Zbl 0954.57018
• [Novikov1970] S. P. Novikov, Algebraic construction and properties of Hermitian analogs of $K$-theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes. I. II, Math. USSR-Izv. 4 (1970), 257–292; ibid. 4 (1970), 479–505; translated from Izv. Akad. Nauk SSSR Ser. Mat. 34 (1970), 253–288; ibid. 34 (1970), 475. MR0292913 (45 #1994) Zbl 0216.45003 Zbl 0233.57009
• [Novikov1970a] S. P. Novikov, Pontrjagin classes, the fundamental group and some problems of stable algebra 1970 Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham) pp. 147–155 Springer, New York. MR0268907 (42 #3804)

• [Novikov2010] S. P. Novikov, Scholarpedia article on the Novikov Conjecture (2010)
• [Ranicki1995] A. A. Ranicki On the Novikov conjecture in [Ferry&Ranicki&Rosenburg1995], 272–337, London Math. Soc. Lecture Note Ser., 226, Cambridge Univ. Press, Cambridge, 1995. MR1388304 (97d:57045) Zbl 0954.57017

3 External links

• The Wikipedia page about the Novikov conjecture.