Manifolds with singularities
Contents |
1 Introduction
Manifolds with singularities are geometric objects in topology generalizing manifolds. They were introduced in ([Sullivan1996],[Sullivan1967]) and [Baas1973]. Applications of the concept include representing cycles in homology theories with coefficients.
2 Definitions
2.1 Cone-like singularities
A manifold with singularities of Baas-Sullivan type is a topological space 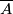 that looks like a manifold outside of a compact 'singularity set', while the singularity set has a neighborhood that looks like the product of manifold and a cone.
Here is a precise definition. Let
that looks like a manifold outside of a compact 'singularity set', while the singularity set has a neighborhood that looks like the product of manifold and a cone.
Here is a precise definition. Let  be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
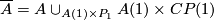
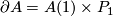
Here,  is a manifold with boundary
is a manifold with boundary 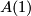 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a definition can be given as follows. For closed manifolds  set
set 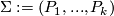 .
.  may be empty. For a subset
may be empty. For a subset 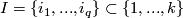 define
define 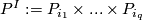 .
.
Def 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
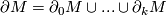 , such that
, such that 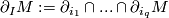 is a manifold for each
is a manifold for each 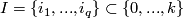 , and such that
, and such that
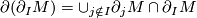
3 Construction and examples
...
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
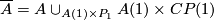
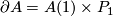
Here,  is a manifold with boundary
is a manifold with boundary 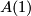 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a definition can be given as follows. For closed manifolds  set
set 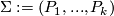 .
.  may be empty. For a subset
may be empty. For a subset 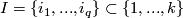 define
define 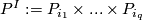 .
.
Def 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
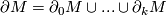 , such that
, such that 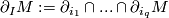 is a manifold for each
is a manifold for each 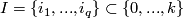 , and such that
, and such that
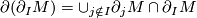
3 Construction and examples
...
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
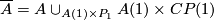
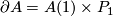
Here,  is a manifold with boundary
is a manifold with boundary 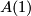 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a definition can be given as follows. For closed manifolds  set
set 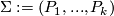 .
.  may be empty. For a subset
may be empty. For a subset 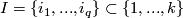 define
define 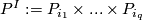 .
.
Def 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
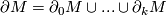 , such that
, such that 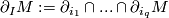 is a manifold for each
is a manifold for each 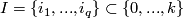 , and such that
, and such that
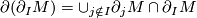
3 Construction and examples
...
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
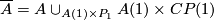
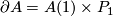
Here,  is a manifold with boundary
is a manifold with boundary 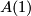 .
.
2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), a definition can be given as follows. For closed manifolds  set
set 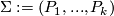 .
.  may be empty. For a subset
may be empty. For a subset 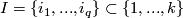 define
define 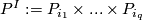 .
.
Def 2.1.A manifold  is a
is a  -Manifold if
-Manifold if
- there is a partition
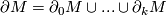 , such that
, such that 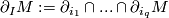 is a manifold for each
is a manifold for each 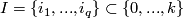 , and such that
, and such that
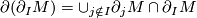
3 Construction and examples
...
4 Invariants
...
5 Classification/Characterization
...
6 Further discussion
...
7 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
|
This page has not been refereed. The information given here might be incomplete or provisional. |