Manifolds with singularities
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
Manifolds with singularities are geometric objects in topology generalizing manifolds. They were introduced in ([Sullivan1996],[Sullivan1967]) and [Baas1973]. Applications of the concept include representing cycles in homology theories with coefficients. All manifolds in this article are understood to be smooth.
[edit] 2 Definitions
[edit] 2.1 Cone-like singularities
A manifold with singularities of Baas-Sullivan type is a topological space 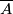 that looks like a manifold outside of a compact 'singularity set', while the singularity set has a neighborhood that looks like the product of manifold and a cone.
Here is a precise definition. Let
that looks like a manifold outside of a compact 'singularity set', while the singularity set has a neighborhood that looks like the product of manifold and a cone.
Here is a precise definition. Let  be a closed manifold. A manifold with a
be a closed manifold. A manifold with a  -singularity (following [Baas1973]) is a space of the form
-singularity (following [Baas1973]) is a space of the form
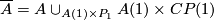
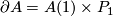
Here,  is a manifold with boundary
is a manifold with boundary 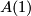 .
.
More complex singularities occur if, instead of taking a cone over only one manifold  , we allow a collection
, we allow a collection  of several closed manifolds. In this case, we define a a manifold with a
of several closed manifolds. In this case, we define a a manifold with a  -singularity to be a (second-countable and Hausdorff) topological space
-singularity to be a (second-countable and Hausdorff) topological space 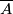 locally homeomorphic to one of the spaces
locally homeomorphic to one of the spaces 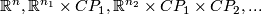 .
.
An alternative approach to manifolds with singularities would be to remove the singular set and to define an equivalence relation on the remaining manifold that 'remembers' the singularities. This view is taken in ([Botvinnik1992],[Botvinnik2001]). We describe it in the next section.
[edit] 2.2  -manifolds
-manifolds
Following ([Botvinnik2001], [Botvinnik1992]), an alternative definition can be given. Let  be a (possibly empty) collection of closed manifolds and denote by
be a (possibly empty) collection of closed manifolds and denote by 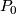 the set containing only one point. Then define
the set containing only one point. Then define 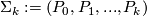 . For a subset
. For a subset 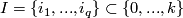 define
define 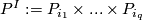 .
.
Definition 2.1.A manifold  is a
is a  -Manifold if there is given
-Manifold if there is given
- a partition
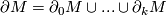 , such that
, such that 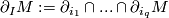 is a manifold for each
is a manifold for each 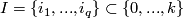 , and such that
, and such that
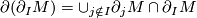
- for each
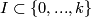 a manifold
a manifold 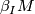 and a diffeomorphism
and a diffeomorphism
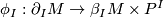
such that if  and
and 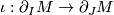 is the inclusion, then the composition
is the inclusion, then the composition
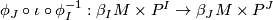
restricts to the identity on the factor 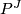 in
in 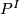 . The diffeomorphisms
. The diffeomorphisms 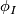 are called product structures.
are called product structures.
On a  -manifold
-manifold  , there is a canonical equivalence relation
, there is a canonical equivalence relation 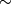 : two points
: two points 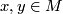 are defined to be equivalent if there is an
are defined to be equivalent if there is an 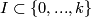 such that
such that 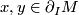 and
and 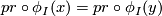 , where
, where 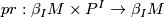 is the projection.
Now we can give a general definition: a manifold with a
is the projection.
Now we can give a general definition: a manifold with a  -singularity is a topological space
-singularity is a topological space 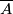 of the form
of the form
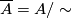
for a  -manifold
-manifold  .
.
The spaces defined above as manifolds with a  -singularity are contained in this new definition. Given manifolds
-singularity are contained in this new definition. Given manifolds  , set
, set 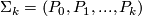 . Removing a neighborhood of the cone-tips in a manifold with
. Removing a neighborhood of the cone-tips in a manifold with  -singularity
-singularity 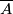 gives a
gives a  -manifold
-manifold  . Now the collapsing of the equivalence relation in
. Now the collapsing of the equivalence relation in  corresponds to the re-attachement of the cone-ends.
corresponds to the re-attachement of the cone-ends.
When dealing with manifolds with singularities it is convenient to work with the underlying  -manifold and make sure that all operations one performs on them are compatible with the equivalence relation.
-manifold and make sure that all operations one performs on them are compatible with the equivalence relation.
[edit] 3 Some examples and constructions
[edit] 3.1 Intersecting spheres
A basic example is presented by two spheres intersecting each other in a sphere of lower dimension. Choose an embedding 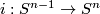 . Then define
. Then define 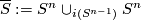 . Outside of the intersecting sphere
. Outside of the intersecting sphere 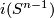 this is an
this is an  -dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of
-dimensional manifold. The intersecting sphere itself has a neigborhood homeomorphic to the product of 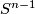 and a cone over
and a cone over 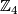 . We can write
. We can write 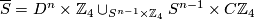 .
.
[edit] 3.2 Inverse images of critical points
Let 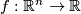 be a Morse-function with
be a Morse-function with  as a single critical point. We can suppose that
as a single critical point. We can suppose that 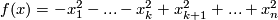 near
near  . Setting
. Setting 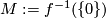 , we see that the cone
, we see that the cone 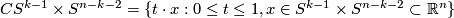 provides a neighborhood of
provides a neighborhood of  in
in  . It follows that
. It follows that  is of the form
is of the form 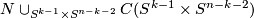 .
.
[edit] 3.3 Structures on manifolds with singularities
Geometric and topological structures that exist for ordinary manifolds can also be defined for manifolds with singularities. This is done in the following way. A manifold with  -singularity
-singularity 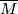 with underlying
with underlying  -manifold
-manifold  carries the structure in question if all manifolds involved in
carries the structure in question if all manifolds involved in 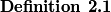 carry this structure and the product diffeomorphisms preserves it.
carry this structure and the product diffeomorphisms preserves it.
For example, 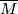 is orientable if
is orientable if  as well as all manifolds in
as well as all manifolds in  and the manifolds
and the manifolds 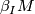 are orientable and the product diffeomorphisms are orientation-preserving. As another example,
are orientable and the product diffeomorphisms are orientation-preserving. As another example, 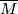 becomes a Riemannian manifold with singularities if we put a Riemannian metric on
becomes a Riemannian manifold with singularities if we put a Riemannian metric on  as well as on the manifolds in
as well as on the manifolds in  and on the manifolds
and on the manifolds 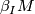 in such a way that the product diffeomorphism are isometries.
in such a way that the product diffeomorphism are isometries.
[edit] 3.4 Bundles on manifolds with singularities
As usual, we define a bundle 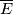 on a manifold with singularities
on a manifold with singularities 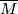 as a bundle
as a bundle  on the underlying manifold
on the underlying manifold  subject to the following additional condition: there are bundles
subject to the following additional condition: there are bundles 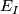 over the manifolds
over the manifolds 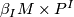 and bundle equivalences
and bundle equivalences 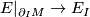 covering the product diffeomorphisms.
covering the product diffeomorphisms.
[edit] 4 Bordism theory for manifolds with singularities
A  -manifold
-manifold  induces the structure of a
induces the structure of a  -manifold on
-manifold on 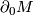 . We call
. We call 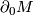 the boundary of
the boundary of  . Given a manifold with a
. Given a manifold with a  -singularity
-singularity 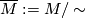 , we define
, we define 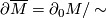 to be its boundary. A theory of bordism with
to be its boundary. A theory of bordism with  -singularities can now be developed just as for ordinary manifolds.
-singularities can now be developed just as for ordinary manifolds.
For illustration we pick up the case of a  -singularity considered above.
-singularity considered above. 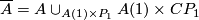 is bordant to zero if there exists
is bordant to zero if there exists 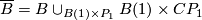 , such that
, such that
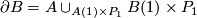
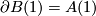
[edit] 5 Invariants
...
[edit] 6 Classification/Characterization
...
[edit] 7 Further discussion
...
[edit] 8 References
- [Baas1973] N. A. Baas, On bordism theory of manifolds with singularities, Math. Scand. 33 (1973), 279–302 (1974). MR0346824 (49 #11547b) Zbl 0281.57027
- [Botvinnik1992] B. I. Botvinnik, Manifolds with singularities and the Adams-Novikov spectral sequence, Cambridge University Press, Cambridge, 1992. MR1192127 (93h:55002) Zbl 0764.55001
- [Botvinnik2001] B. Botvinnik, Manifolds with singularities accepting a metric of positive scalar curvature, Geom. Topol. 5 (2001), 683–718 (electronic). MR1857524 (2002j:57045) Zbl 1002.57055
- [Sullivan1967] D. Sullivan, On the Hauptvermutung for manifolds, Bull. Amer. Math. Soc. 73 (1967), 598–600. MR0212811 (35 #3676) Zbl 0153.54002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021