Linking form
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Background: intersection forms
After Poincaré and Lefschetz, a closed oriented manifold 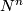 has a bilinear intersection form defined on its homology. Given a
has a bilinear intersection form defined on its homology. Given a 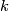 --chain
--chain 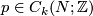 and an
and an 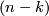 --chain
--chain 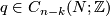 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 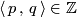 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
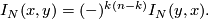
2 Definition of the linking form
 is the subgroup
is the subgroup 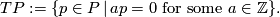
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 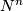 is the bilinear
is the bilinear 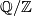 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
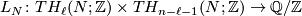
such that
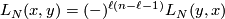
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 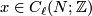 and
and 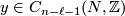 , let
, let 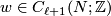 be such that
be such that 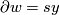 , for some
, for some 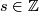 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 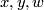 and
and  .
.
3 Definition via homology
Let 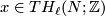 and let
and let 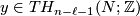 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
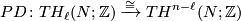
and
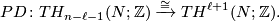
Associated to the short exact sequence of coefficients
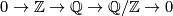
is the Bockstein long exact sequence in cohomology.
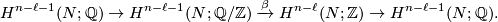
Choose 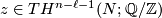 such that
such that 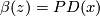 . This is always possible since torsion elements in
. This is always possible since torsion elements in 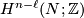 map to zero in
map to zero in 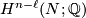 . There is a cup product:
. There is a cup product:
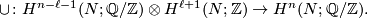
Compute 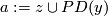 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
yields 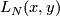 .
.
4 Example of 3-dimensional projective space
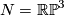 , so that
, so that 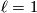 and
and  . Now
. Now 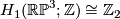 . Let
. Let 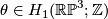 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 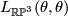 , consider
, consider 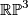 modelled as
modelled as 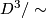 , with antipodal points on
, with antipodal points on 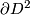 identified, and choose two representative
identified, and choose two representative  -chains
-chains Tex syntax errorand
Tex syntax errorfor
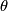 . Let
. Let Tex syntax errorbe the straight line between north and south poles and let
Tex syntax errorbe half of the equator. Now
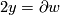 , where
, where 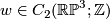 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 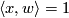 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 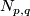 has
has 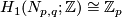 . The linking form is given on a generator
. The linking form is given on a generator 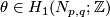 by
by 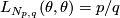 . Note that
. Note that 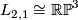 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 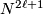
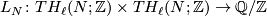
is an exact sequence:
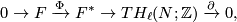
where  is a free abelain group and the linking
is a free abelain group and the linking 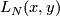 can be computed as follows. Let
can be computed as follows. Let 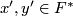 be such that
be such that 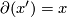 and
and 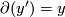 . Then we can tensor with
. Then we can tensor with 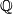 to obtain an isomorphism
to obtain an isomorphism
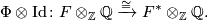
The linking form is given by:
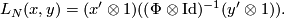
Let 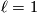 , so
, so 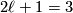 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. The matrix
is a rational homology 3-sphere. The matrix  of (self-) linking numbers of the link determines a presentation of the linking form of
of (self-) linking numbers of the link determines a presentation of the linking form of  . Taking the number of link components in the surgery presentation for
. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 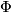 as above. The intersection form on a simply connected 4-manifold
as above. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~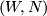 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401
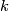 --chain
--chain 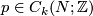 and an
and an 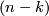 --chain
--chain 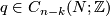 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 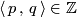 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
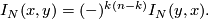
2 Definition of the linking form
 is the subgroup
is the subgroup 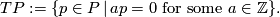
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 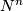 is the bilinear
is the bilinear 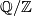 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
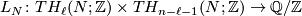
such that
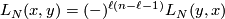
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 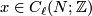 and
and 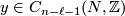 , let
, let 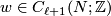 be such that
be such that 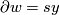 , for some
, for some 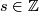 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 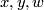 and
and  .
.
3 Definition via homology
Let 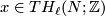 and let
and let 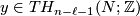 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
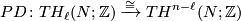
and
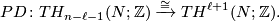
Associated to the short exact sequence of coefficients
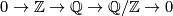
is the Bockstein long exact sequence in cohomology.
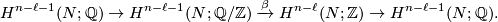
Choose 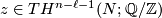 such that
such that 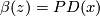 . This is always possible since torsion elements in
. This is always possible since torsion elements in 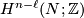 map to zero in
map to zero in 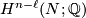 . There is a cup product:
. There is a cup product:
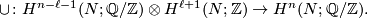
Compute 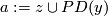 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
yields 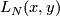 .
.
4 Example of 3-dimensional projective space
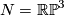 , so that
, so that 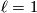 and
and  . Now
. Now 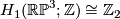 . Let
. Let 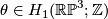 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 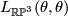 , consider
, consider 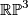 modelled as
modelled as 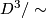 , with antipodal points on
, with antipodal points on 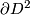 identified, and choose two representative
identified, and choose two representative  -chains
-chains Tex syntax errorand
Tex syntax errorfor
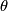 . Let
. Let Tex syntax errorbe the straight line between north and south poles and let
Tex syntax errorbe half of the equator. Now
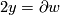 , where
, where 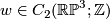 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 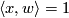 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 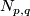 has
has 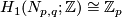 . The linking form is given on a generator
. The linking form is given on a generator 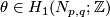 by
by 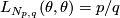 . Note that
. Note that 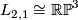 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 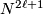
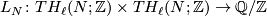
is an exact sequence:
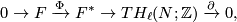
where  is a free abelain group and the linking
is a free abelain group and the linking 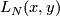 can be computed as follows. Let
can be computed as follows. Let 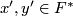 be such that
be such that 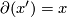 and
and 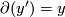 . Then we can tensor with
. Then we can tensor with 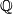 to obtain an isomorphism
to obtain an isomorphism
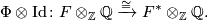
The linking form is given by:
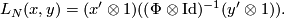
Let 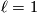 , so
, so 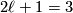 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. The matrix
is a rational homology 3-sphere. The matrix  of (self-) linking numbers of the link determines a presentation of the linking form of
of (self-) linking numbers of the link determines a presentation of the linking form of  . Taking the number of link components in the surgery presentation for
. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 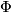 as above. The intersection form on a simply connected 4-manifold
as above. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~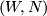 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401
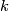 --chain
--chain 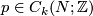 and an
and an 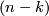 --chain
--chain 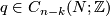 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 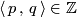 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
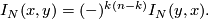
2 Definition of the linking form
 is the subgroup
is the subgroup 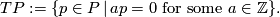
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 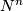 is the bilinear
is the bilinear 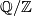 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
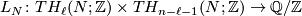
such that
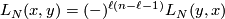
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 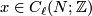 and
and 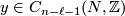 , let
, let 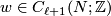 be such that
be such that 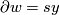 , for some
, for some 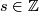 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 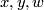 and
and  .
.
3 Definition via homology
Let 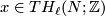 and let
and let 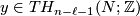 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
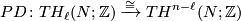
and
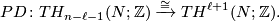
Associated to the short exact sequence of coefficients
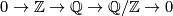
is the Bockstein long exact sequence in cohomology.
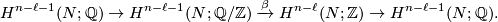
Choose 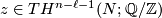 such that
such that 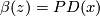 . This is always possible since torsion elements in
. This is always possible since torsion elements in 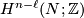 map to zero in
map to zero in 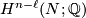 . There is a cup product:
. There is a cup product:
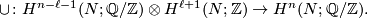
Compute 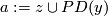 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
yields 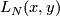 .
.
4 Example of 3-dimensional projective space
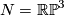 , so that
, so that 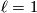 and
and  . Now
. Now 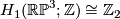 . Let
. Let 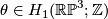 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 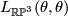 , consider
, consider 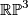 modelled as
modelled as 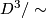 , with antipodal points on
, with antipodal points on 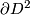 identified, and choose two representative
identified, and choose two representative  -chains
-chains Tex syntax errorand
Tex syntax errorfor
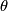 . Let
. Let Tex syntax errorbe the straight line between north and south poles and let
Tex syntax errorbe half of the equator. Now
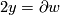 , where
, where 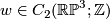 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 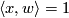 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 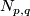 has
has 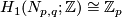 . The linking form is given on a generator
. The linking form is given on a generator 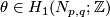 by
by 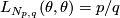 . Note that
. Note that 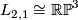 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 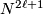
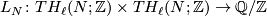
is an exact sequence:
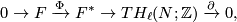
where  is a free abelain group and the linking
is a free abelain group and the linking 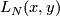 can be computed as follows. Let
can be computed as follows. Let 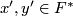 be such that
be such that 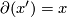 and
and 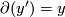 . Then we can tensor with
. Then we can tensor with 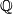 to obtain an isomorphism
to obtain an isomorphism
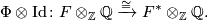
The linking form is given by:
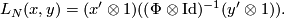
Let 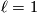 , so
, so 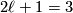 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. The matrix
is a rational homology 3-sphere. The matrix  of (self-) linking numbers of the link determines a presentation of the linking form of
of (self-) linking numbers of the link determines a presentation of the linking form of  . Taking the number of link components in the surgery presentation for
. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 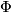 as above. The intersection form on a simply connected 4-manifold
as above. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~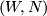 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401
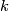 --chain
--chain 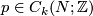 and an
and an 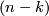 --chain
--chain 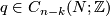 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 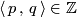 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
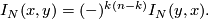
2 Definition of the linking form
 is the subgroup
is the subgroup 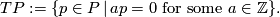
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 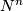 is the bilinear
is the bilinear 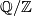 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
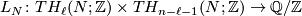
such that
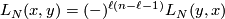
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 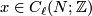 and
and 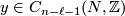 , let
, let 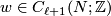 be such that
be such that 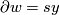 , for some
, for some 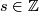 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 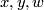 and
and  .
.
3 Definition via homology
Let 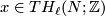 and let
and let 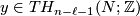 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
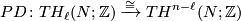
and
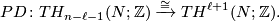
Associated to the short exact sequence of coefficients
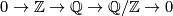
is the Bockstein long exact sequence in cohomology.
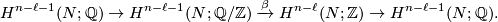
Choose 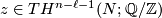 such that
such that 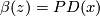 . This is always possible since torsion elements in
. This is always possible since torsion elements in 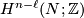 map to zero in
map to zero in 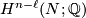 . There is a cup product:
. There is a cup product:
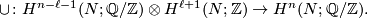
Compute 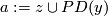 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
yields 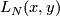 .
.
4 Example of 3-dimensional projective space
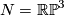 , so that
, so that 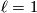 and
and  . Now
. Now 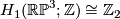 . Let
. Let 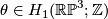 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 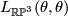 , consider
, consider 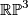 modelled as
modelled as 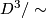 , with antipodal points on
, with antipodal points on 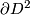 identified, and choose two representative
identified, and choose two representative  -chains
-chains Tex syntax errorand
Tex syntax errorfor
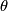 . Let
. Let Tex syntax errorbe the straight line between north and south poles and let
Tex syntax errorbe half of the equator. Now
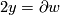 , where
, where 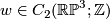 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 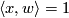 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 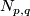 has
has 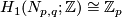 . The linking form is given on a generator
. The linking form is given on a generator 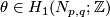 by
by 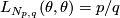 . Note that
. Note that 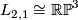 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 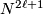
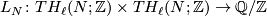
is an exact sequence:
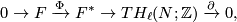
where  is a free abelain group and the linking
is a free abelain group and the linking 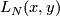 can be computed as follows. Let
can be computed as follows. Let 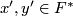 be such that
be such that 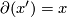 and
and 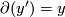 . Then we can tensor with
. Then we can tensor with 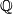 to obtain an isomorphism
to obtain an isomorphism
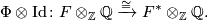
The linking form is given by:
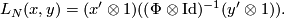
Let 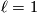 , so
, so 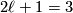 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. The matrix
is a rational homology 3-sphere. The matrix  of (self-) linking numbers of the link determines a presentation of the linking form of
of (self-) linking numbers of the link determines a presentation of the linking form of  . Taking the number of link components in the surgery presentation for
. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 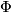 as above. The intersection form on a simply connected 4-manifold
as above. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~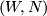 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401