Linking form
Markpowell13 (Talk | contribs) (→Introduction to linking forms) |
Markpowell13 (Talk | contribs) |
||
| Line 15: | Line 15: | ||
== Definition of the linking form== | == Definition of the linking form== | ||
| − | By bilinearity, the intersection form vanishes on the torsion part of the homology. The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold $N^n$ is the bilinear $\mathbb{Q}/\mathbb{Z}$--valued linking form, which is due to Seifert: | + | By bilinearity, the intersection form vanishes on the torsion part of the homology. The torsion part of an abelian group $P$ is the set $$TP:= \{p \in P \,|\, ap=0 \text{ for some } a \in \mathbb{Z}\}.$$ |
| + | |||
| + | The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold $N^n$ is the bilinear $\mathbb{Q}/\mathbb{Z}$--valued linking form, which is due to Seifert: | ||
$$L_N \colon TH_{\ell}(N;\mathbb{Z}) \times TH_{n-\ell-1}(N;\mathbb{Z}) \to \mathbb{Q}/\mathbb{Z}$$ | $$L_N \colon TH_{\ell}(N;\mathbb{Z}) \times TH_{n-\ell-1}(N;\mathbb{Z}) \to \mathbb{Q}/\mathbb{Z}$$ | ||
such that | such that | ||
| − | $$L_N(x,y) = (-)^{\ell(n-\ell-1)}L_N(y,x) | + | $$L_N(x,y) = (-)^{\ell(n-\ell-1)}L_N(y,x)$$ |
| − | + | and computed as follows. Given $[x] \in TH_\ell(N;\mathbb{Z})$ and $[y] \in TH_{n-\ell-1}(N;\mathbb{Z})$ represented by cycles $x \in C_\ell(N;\mathbb{Z})$ and $y \in C_{n-\ell-1}(N,\mathbb{Z})$, let $w \in C_{\ell+1}(N;\mathbb{Z})$ be such that $\partial w = sy$, for some $s \in \mathbb{Z}$. Then we define: | |
| − | + | ||
| − | Given $[x] \in TH_\ell(N;\mathbb{Z})$ and $[y] \in TH_{n-\ell-1}(N;\mathbb{Z})$ represented by cycles $x \in C_\ell(N;\mathbb{Z})$ and $y \in C_{n-\ell-1}(N,\mathbb{Z})$, let $w \in C_{\ell+1}(N;\mathbb{Z})$ be such that $\partial w = sy$, for some $s \in \mathbb{Z}$. Then we define: | + | |
$$L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.$$ | $$L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.$$ | ||
The resulting element is independent of the choices of $x,y,w$ and $s$. | The resulting element is independent of the choices of $x,y,w$ and $s$. | ||
Revision as of 16:00, 27 March 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Background: intersection forms
After Poincaré and Lefschetz, a closed oriented manifold 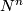 has a bilinear intersection form defined on its homology. Given a
has a bilinear intersection form defined on its homology. Given a 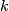 --chain
--chain 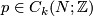 and an
and an 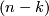 --chain
--chain 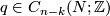 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 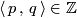 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
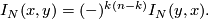
2 Definition of the linking form
By bilinearity, the intersection form vanishes on the torsion part of the homology. The torsion part of an abelian group is the set
is the set 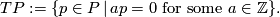
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 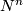 is the bilinear
is the bilinear 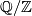 --valued linking form, which is due to Seifert:
--valued linking form, which is due to Seifert:
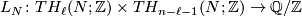
such that
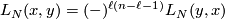
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 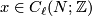 and
and 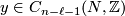 , let
, let 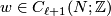 be such that
be such that 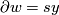 , for some
, for some 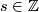 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 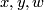 and
and  .
.
As an example, let 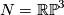 , so that
, so that 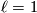 and
and  . Now
. Now 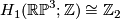 . Let
. Let 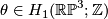 be the non--trivial element. To compute the linking
be the non--trivial element. To compute the linking 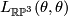 , consider
, consider 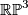 modelled as
modelled as 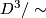 , with antipodal points on
, with antipodal points on 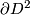 identified, and choose two representative
identified, and choose two representative  --chains
--chains  and
and  for
for 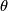 . Let
. Let  be the straight line between north and south poles and let
be the straight line between north and south poles and let  be half of the equator. Now
be half of the equator. Now 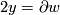 , where
, where 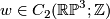 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 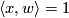 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
3 References
$--chains $x$ and $y$ for $\theta$. Let $x$ be the straight line between north and south poles and let $y$ be half of the equator. Now y = \partial w$, where $w \in C_2(\mathbb{RP}^3;\mathbb{Z})$ is the 2-disk whose boundary is the equator. We see that $\langle x,w \rangle = 1$, so that $$L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.$$ == References == {{#RefList:}} [[Category:Theory]] [[Category:Definitions]]N^{n} has a bilinear intersection form defined on its homology. Given a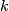 --chain
--chain 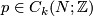 and an
and an 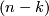 --chain
--chain 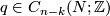 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 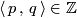 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
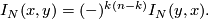
2 Definition of the linking form
By bilinearity, the intersection form vanishes on the torsion part of the homology. The torsion part of an abelian group is the set
is the set 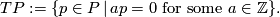
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 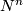 is the bilinear
is the bilinear 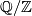 --valued linking form, which is due to Seifert:
--valued linking form, which is due to Seifert:
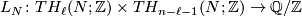
such that
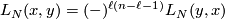
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 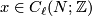 and
and 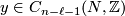 , let
, let 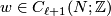 be such that
be such that 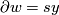 , for some
, for some 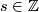 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 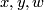 and
and  .
.
As an example, let 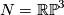 , so that
, so that 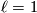 and
and  . Now
. Now 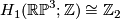 . Let
. Let 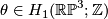 be the non--trivial element. To compute the linking
be the non--trivial element. To compute the linking 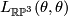 , consider
, consider 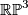 modelled as
modelled as 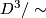 , with antipodal points on
, with antipodal points on 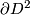 identified, and choose two representative
identified, and choose two representative  --chains
--chains  and
and  for
for 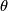 . Let
. Let  be the straight line between north and south poles and let
be the straight line between north and south poles and let  be half of the equator. Now
be half of the equator. Now 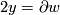 , where
, where 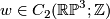 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 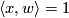 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)