Lie groups I: Definition and examples
From Manifold Atlas
|
This page has not been refereed. The information given here might be incomplete or provisional.
|
1 Introduction
-
This is part I of a series of articles about Lie groups.
We define Lie groups and homomorphisms and give the most important examples. In following pages of this series we define the fundamental invariants like the Dynkin diagram, and report about the classification of compact Lie groups. We also report about exceptional Lie groups.
2 Definition and examples
-
Definition 2.1. A Lie group is a finite dimensional smooth manifold  together with a group structure on
together with a group structure on  , such that the multiplication
, such that the multiplication 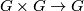 and the attaching of an inverse
and the attaching of an inverse 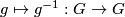 are smooth maps.
are smooth maps.
A morphism between two Lie groups

and

is a map
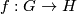
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map

such that

and
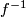
are morphisms. A Lie subgroup is a subgroup

in

such that

is also a smooth submanifold of

.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 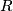 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 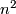 ,
, 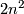 and
and 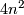 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices

, the
orthogonal group, the hermitian matrices
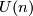
, the
unitary group, and the symplectic matrices

, the
symplectic group. The way to see this is to consider the map
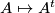
from
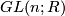
to the vector space of symmetric matrices and to show that the unit matrix

is a regular value. Thus the preimage of

, which is

is a smooth submanifold and so

is a Lie submanifold of
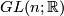
. Similarly one considers the map
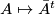
from

to the skew symmetric matrices over

and shows again that

is a regular value. The dimension of

is
and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group

is not the group of isometries of a non-degenerate skew-symmetric

-bilinear form, but the group of the hermitian form on
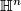
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of

is

, thus we don't consider the groups
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 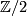 [???] generated by the inclusion
[???] generated by the inclusion 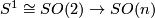 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 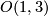 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 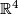 given by
given by 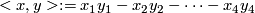 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper 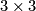 matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 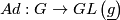 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 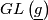 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 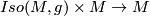 mapping
mapping 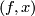 to
to 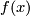 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 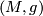 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 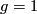 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
$-dimensional Lie group. In particular all finite groups are together with a group structure on

, such that the multiplication
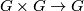
and the attaching of an inverse
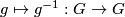
are smooth maps.
A morphism between two Lie groups

and

is a map
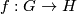
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map

such that

and
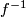
are morphisms. A Lie subgroup is a subgroup

in

such that

is also a smooth submanifold of

.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 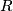 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 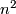 ,
, 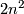 and
and 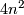 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices

, the
orthogonal group, the hermitian matrices
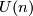
, the
unitary group, and the symplectic matrices

, the
symplectic group. The way to see this is to consider the map
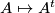
from
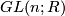
to the vector space of symmetric matrices and to show that the unit matrix

is a regular value. Thus the preimage of

, which is

is a smooth submanifold and so

is a Lie submanifold of
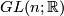
. Similarly one considers the map
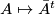
from

to the skew symmetric matrices over

and shows again that

is a regular value. The dimension of

is
and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group

is not the group of isometries of a non-degenerate skew-symmetric

-bilinear form, but the group of the hermitian form on
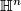
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of

is

, thus we don't consider the groups
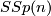
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 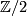 [???] generated by the inclusion
[???] generated by the inclusion 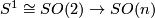 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 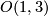 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on  given by
given by 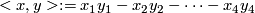 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper  matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 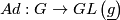 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 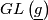 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 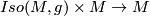 mapping
mapping 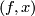 to
to 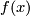 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 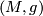 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 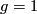 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
$-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over $R$, $\mathbb C$ or the quternions $\mathbb H$:
$$GL(n;\mathbb R) ; \,\, GL(n;\mathbb C);GL(n;\mathbb H),$$ are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is $n^2$, n^2$ and n^2$ resp. (note that Lie groups are real manifolds, this explains the formula for the dimension). $GL(n;\mathbb C)$ is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices $O(n)$, the '''orthogonal group''', the hermitian matrices $U(n)$, the '''unitary group''', and the symplectic matrices $Sp(n)$, the '''symplectic group'''. The way to see this is to consider the map $A \mapsto A^t$ from $GL(n;R)$ to the vector space of symmetric matrices and to show that the unit matrix $E$ is a regular value. Thus the preimage of $E$, which is $O(n)$ is a smooth submanifold and so $O(n)$ is a Lie submanifold of $GL(n;\mathbb R)$. Similarly one considers the map $A \mapsto \bar A^t$ from $GL(n;\mathbb C)$ to the skew symmetric matrices over $\mathbb C$ and shows again that $E$ is a regular value. The dimension of $O(n)$ is $$ \dim O(n) = n^2 - \frac{n(n+1)}{2} = \frac{n(n-1)}{2}$$ and
$$\dim U(n) =2n^2-( n + \frac{2n(n-1)}{2}) = n^2.$$
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant G together with a group structure on

, such that the multiplication
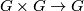
and the attaching of an inverse
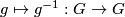
are smooth maps.
A morphism between two Lie groups

and

is a map
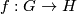
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map

such that

and
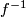
are morphisms. A Lie subgroup is a subgroup

in

such that

is also a smooth submanifold of

.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 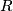 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 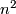 ,
, 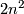 and
and 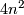 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices

, the
orthogonal group, the hermitian matrices
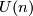
, the
unitary group, and the symplectic matrices

, the
symplectic group. The way to see this is to consider the map
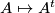
from
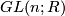
to the vector space of symmetric matrices and to show that the unit matrix

is a regular value. Thus the preimage of

, which is

is a smooth submanifold and so

is a Lie submanifold of
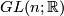
. Similarly one considers the map
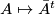
from

to the skew symmetric matrices over

and shows again that

is a regular value. The dimension of

is
and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group

is not the group of isometries of a non-degenerate skew-symmetric

-bilinear form, but the group of the hermitian form on
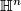
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of

is

, thus we don't consider the groups
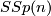
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 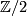 [???] generated by the inclusion
[???] generated by the inclusion 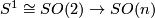 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 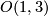 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on  given by
given by 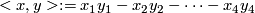 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper  matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 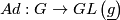 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 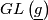 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 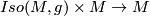 mapping
mapping 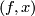 to
to 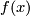 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 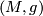 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 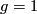 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
$, the '''special orthogonal group''' or '''special unitary group''':
$$
SO(n); SU(n).
$$
The first is just the component of $E$ in $O(n)$, whereas the second is the preimage of the regular value G together with a group structure on

, such that the multiplication
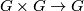
and the attaching of an inverse
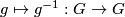
are smooth maps.
A morphism between two Lie groups

and

is a map
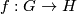
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map

such that

and
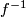
are morphisms. A Lie subgroup is a subgroup

in

such that

is also a smooth submanifold of

.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 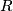 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 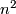 ,
, 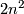 and
and 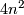 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices  , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 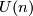 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 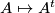 from
from 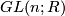 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 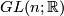 . Similarly one considers the map
. Similarly one considers the map 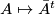 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is and
is and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group  is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 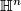
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of  is
is  , thus we don't consider the groups
, thus we don't consider the groups 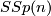 .
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 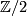 [???] generated by the inclusion
[???] generated by the inclusion 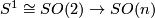 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 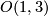 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on  given by
given by 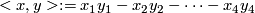 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper  matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 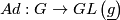 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 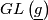 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 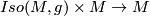 mapping
mapping 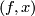 to
to 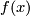 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 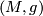 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 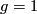 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
$ in $S^1$ and so has codimension G together with a group structure on  , such that the multiplication
, such that the multiplication 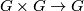 and the attaching of an inverse
and the attaching of an inverse 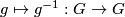 are smooth maps.
A morphism between two Lie groups
are smooth maps.
A morphism between two Lie groups  and
and  is a map
is a map 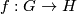 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and  are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 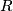 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 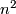 ,
, 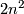 and
and 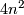 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices  , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 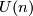 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 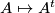 from
from 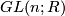 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 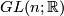 . Similarly one considers the map
. Similarly one considers the map 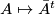 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is and
is and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group  is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 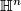
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of  is
is  , thus we don't consider the groups
, thus we don't consider the groups 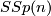 .
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 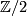 [???] generated by the inclusion
[???] generated by the inclusion 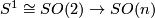 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 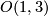 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 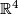 given by
given by 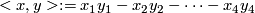 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper  matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 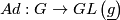 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 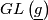 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 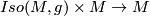 mapping
mapping 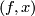 to
to 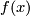 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 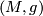 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 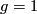 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
$, implying:
$$\dim SU(n) = n^2-1.$$ The symplectic group $Sp(n)$ is not the group of isometries of a non-degenerate skew-symmetric $\mathbb H$-bilinear form, but the group of the hermitian form on $\mathbb H^n$
$$ := \bar x_1y_1 + \dots + \bar x_ny_n.
$$
With this definition one proceeds as in the examples above and show that $Sp(n)$ is a Lie group of dimension
$$
\dim Sp(n) = n(2n+1).
$$ The determinant of an element of $Sp(n)$ is G together with a group structure on  , such that the multiplication
, such that the multiplication 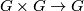 and the attaching of an inverse
and the attaching of an inverse 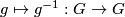 are smooth maps.
A morphism between two Lie groups
are smooth maps.
A morphism between two Lie groups  and
and  is a map
is a map 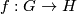 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 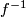 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 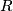 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 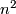 ,
, 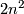 and
and 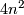 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices  , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 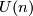 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 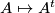 from
from 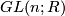 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 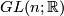 . Similarly one considers the map
. Similarly one considers the map 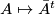 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is and
is and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group  is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 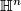
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of  is
is  , thus we don't consider the groups
, thus we don't consider the groups 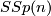 .
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 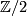 [???] generated by the inclusion
[???] generated by the inclusion 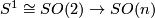 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 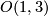 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 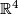 given by
given by 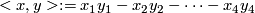 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper 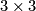 matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 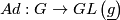 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 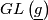 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 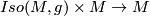 mapping
mapping 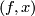 to
to 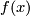 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 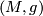 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 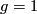 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
$, thus we don't consider the groups $SSp(n)$.
As mentioned above $SO(n)$ is the component of $E$ in $O(n)$. For $n>2$ it's fundamental group is $\mathbb Z/2$ \cite{???} generated by the inclusion $S^1 \cong SO(2) \to SO(n)$. If $G$ is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of $SO(n)$ for $n>2$ is a Lie group denoted by $Spin(n)$, the '''Spinor group'''. There is a more explicit construction of $Spin(n)$ in terms of Clifford algebras \cite{???}.
Some of the low dimensional Lie groups above occur in two or more ways, for example $$SO(2) \cong U(1) = S^1, \,\, SU(2) \cong Spin(3) \cong Sp(1) \ = S^3.$$
A special role in the world of Lie groups play the '''tori''', the Lie groups
$$T^n := (S^1)^n.$$ As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The ''Lorentz group'' $O(1,3)$ the group of the isometries of the Minkowski space, the isometries of the form on $\mathbb R^4$ given by $ := x_1y_1 - x_2y_2 - \dots - x_4y_4$. It's dimension is $.
2.) The Heisenberg Group $H $ consisting of upper \times 3$ matrices with diagonal entries G together with a group structure on  , such that the multiplication
, such that the multiplication 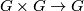 and the attaching of an inverse
and the attaching of an inverse 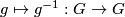 are smooth maps.
A morphism between two Lie groups
are smooth maps.
A morphism between two Lie groups  and
and  is a map
is a map 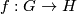 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 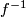 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 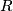 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 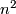 ,
, 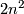 and
and 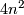 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices  , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 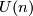 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 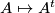 from
from 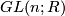 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 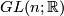 . Similarly one considers the map
. Similarly one considers the map 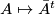 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is and
is and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group  is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 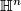
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of  is
is  , thus we don't consider the groups
, thus we don't consider the groups 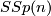 .
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 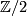 [???] generated by the inclusion
[???] generated by the inclusion 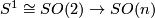 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 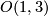 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 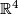 given by
given by 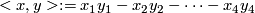 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper 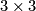 matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 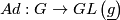 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 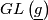 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 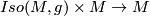 mapping
mapping 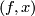 to
to 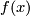 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 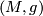 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 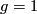 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
$. It's dimension is $.
The following theorems give a rough picture of all Lie groups:
{{beginthm|Theorem}} Assume that the Lie group $G$ is semisimple. Then $G$ is isomorphic to a Lie subgroup of $GL(n;\mathbb R)$ for some $n$ \cite{???}.
{{endthm}}
Proof: Let $Ad:G\rightarrow GL\left(\underline{g}\right)$ be the [[Wikipedia:Adjoint_representation_of_a_Lie_group|Adjoint representation]] of $G$. If $G$ is semisimple, then the adjoint representation is faithful, thus $G$ is mapped isomorphically to a subgroup of $GL\left(\underline{g}\right)$.
{{beginthm|Theorem}} A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace \cite{???}.
{{endthm}}
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
== Further discussion ==
;
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying '''symmetries'''. Given a geometric object, say a closed smooth manifold $M$ with a Riemannian metric $g$, then one can consider the group of self isometries $Iso(M,g)$. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map $Iso(M,g) \times M \to M$ mapping $(f,x)$ to $f(x)$ is a smooth map \cite{Kobayashi transformation groups ...}. Thus we have a smooth action of $Iso(M,g)$ on $M$. The size of this group is a measure for the symmetry of $(M,g)$. In turn if a compact Lie group $G$ acts smoothly on a closed smooth manifold $M$, then there is a Riemannian metric on $M$ such that $G$ acts by isometries (choose an arbitrary Riemannian metric and average it over $G$ using a Haar measure). If the action is effective (meaning that if $g$ acts trivially, the $g =1$), then $G$ is a subgroup of $Iso(M,g)$.
Motivated by these considerations one defines an invariant for closed smooth manifolds$M$, the '''degree of symmetry''' which is the largest dimension of a compact Lie group acting effectively on $M$ (or equivalently the largest dimension of $Iso(M,g)$ as $g$ varies over all Riemannian metrics of $M$). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
{{beginthm|Theorem \cite{Frobenius-Birkhoff}}} The degree of symmetry of a clsoed manifold $M$ of dimension $m$ is $\le \frac{m(m+1)}{2}$ (the dimension of $O(m+1)$, which acts on $S^m$), and if the degree of symmetry is $\frac{m(m+1)}{2}$ then $M$ is diffeomorphic to $S^m$ or $\mathbb {RP}^m$.
{{endthm}}
== References ==
{{#RefList:}}
[[Category:Manifolds]]G together with a group structure on  , such that the multiplication
, such that the multiplication 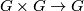 and the attaching of an inverse
and the attaching of an inverse 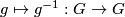 are smooth maps.
A morphism between two Lie groups
are smooth maps.
A morphism between two Lie groups  and
and  is a map
is a map 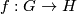 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 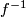 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
.
It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 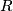 ,
,  or the quternions
or the quternions  :
:
are Lie groups.
They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 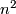 ,
, 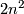 and
and 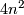 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
All these groups are non-compact (for positive dimensions). They contain compact Lie subgroups given by the orthogonal matrices  , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 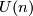 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 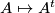 from
from 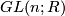 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 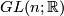 . Similarly one considers the map
. Similarly one considers the map 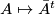 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is and
is and
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
The first is just the component of  in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
The symplectic group  is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 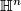
With this definition one proceeds as in the examples above and show that  is a Lie group of dimension
is a Lie group of dimension
The determinant of an element of  is
is  , thus we don't consider the groups
, thus we don't consider the groups 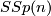 .
.
As mentioned above  is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 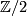 [???] generated by the inclusion
[???] generated by the inclusion 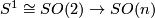 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
Some of the low dimensional Lie groups above occur in two or more ways, for example
A special role in the world of Lie groups play the tori, the Lie groups
As we will discuss in a later page, a connected abelian Lie group is isomorphic to a torus.
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 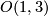 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 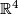 given by
given by 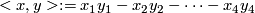 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper 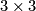 matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Proof: Let 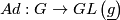 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 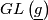 .
.
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
Further discussion
-
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 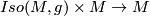 mapping
mapping 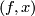 to
to 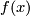 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 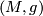 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 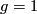 ), then
), then  is a subgroup of
is a subgroup of  .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
3 References
 together with a group structure on
together with a group structure on  , such that the multiplication
, such that the multiplication 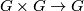 and the attaching of an inverse
and the attaching of an inverse 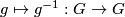 are smooth maps.
are smooth maps.
 and
and  is a map
is a map 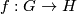 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 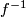 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
. -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 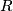 ,
,  or the quternions
or the quternions  :
:
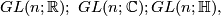
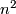 ,
, 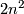 and
and 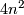 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
 , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 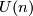 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 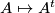 from
from 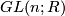 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 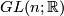 . Similarly one considers the map
. Similarly one considers the map 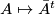 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is
is 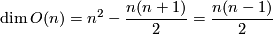
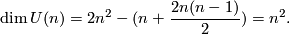
 , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
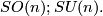
 in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
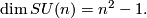
 is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 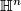
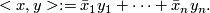
 is a Lie group of dimension
is a Lie group of dimension
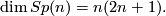
 is
is  , thus we don't consider the groups
, thus we don't consider the groups 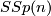 .
.
 is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is  [???] generated by the inclusion
[???] generated by the inclusion 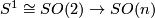 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
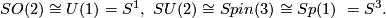
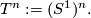
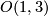 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on  given by
given by 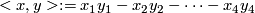 . It's dimension is
. It's dimension is  .
.
 consisting of upper
consisting of upper  matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
 is semisimple. Then
is semisimple. Then  is isomorphic to a Lie subgroup of
is isomorphic to a Lie subgroup of 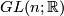 for some
for some  [???].
[???].
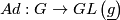 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 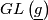 .
.
 with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 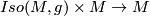 mapping
mapping 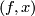 to
to 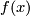 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 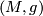 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 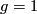 ), then
), then  is a subgroup of
is a subgroup of  .
.
 , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
 of dimension
of dimension  is
is 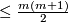 (the dimension of
(the dimension of 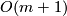 , which acts on
, which acts on 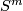 ), and if the degree of symmetry is
), and if the degree of symmetry is 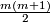 then
then  is diffeomorphic to
is diffeomorphic to 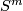 or
or 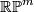 .
.
 , such that the multiplication
, such that the multiplication 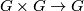 and the attaching of an inverse
and the attaching of an inverse 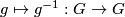 are smooth maps.
A morphism between two Lie groups
are smooth maps.
A morphism between two Lie groups  and
and  is a map
is a map 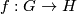 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 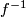 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
. -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 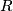 ,
,  or the quternions
or the quternions  :
:
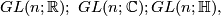
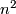 ,
, 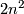 and
and 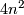 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
 , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 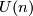 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 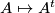 from
from 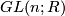 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 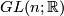 . Similarly one considers the map
. Similarly one considers the map 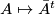 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is
is 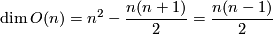
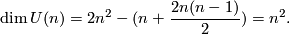
 , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
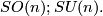
 in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
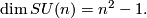
 is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 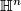
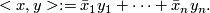
 is a Lie group of dimension
is a Lie group of dimension
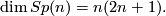
 is
is  , thus we don't consider the groups
, thus we don't consider the groups 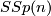 .
.
 is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is  [???] generated by the inclusion
[???] generated by the inclusion 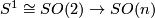 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
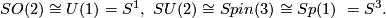
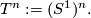
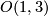 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 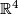 given by
given by 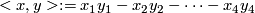 . It's dimension is
. It's dimension is  .
.
 consisting of upper
consisting of upper  matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
 is semisimple. Then
is semisimple. Then  is isomorphic to a Lie subgroup of
is isomorphic to a Lie subgroup of 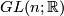 for some
for some  [???].
[???].
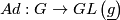 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 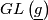 .
.
 with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 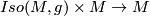 mapping
mapping 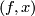 to
to 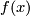 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 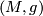 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 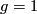 ), then
), then  is a subgroup of
is a subgroup of  .
.
 , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
 of dimension
of dimension  is
is 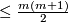 (the dimension of
(the dimension of 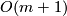 , which acts on
, which acts on 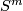 ), and if the degree of symmetry is
), and if the degree of symmetry is 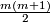 then
then  is diffeomorphic to
is diffeomorphic to 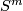 or
or 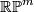 .
.
 , such that the multiplication
, such that the multiplication 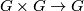 and the attaching of an inverse
and the attaching of an inverse 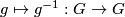 are smooth maps.
A morphism between two Lie groups
are smooth maps.
A morphism between two Lie groups  and
and  is a map
is a map 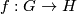 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 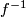 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
. -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over 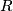 ,
,  or the quternions
or the quternions  :
:
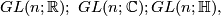
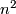 ,
, 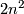 and
and 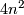 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).  is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
 , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 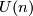 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices  , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 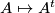 from
from 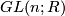 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is  is a smooth submanifold and so
is a smooth submanifold and so  is a Lie submanifold of
is a Lie submanifold of 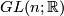 . Similarly one considers the map
. Similarly one considers the map 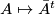 from
from  to the skew symmetric matrices over
to the skew symmetric matrices over  and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of  is
is 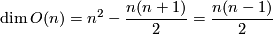
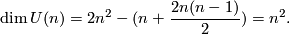
 , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
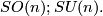
 in
in  , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
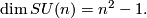
 is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 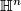
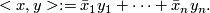
 is a Lie group of dimension
is a Lie group of dimension
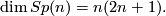
 is
is  , thus we don't consider the groups
, thus we don't consider the groups 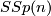 .
.
 is the component of
is the component of  in
in  . For
. For  it's fundamental group is
it's fundamental group is 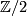 [???] generated by the inclusion
[???] generated by the inclusion 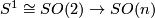 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of  for
for  is a Lie group denoted by
is a Lie group denoted by  , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of  in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
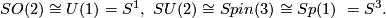
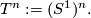
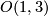 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 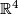 given by
given by 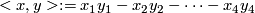 . It's dimension is
. It's dimension is  .
.
 consisting of upper
consisting of upper  matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
 is semisimple. Then
is semisimple. Then  is isomorphic to a Lie subgroup of
is isomorphic to a Lie subgroup of 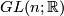 for some
for some  [???].
[???].
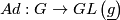 be the Adjoint representation of
be the Adjoint representation of  . If
. If  is semisimple, then the adjoint representation is faithful, thus
is semisimple, then the adjoint representation is faithful, thus  is mapped isomorphically to a subgroup of
is mapped isomorphically to a subgroup of 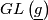 .
.
 with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries  . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 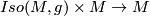 mapping
mapping 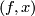 to
to 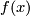 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of  on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 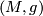 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 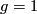 ), then
), then  is a subgroup of
is a subgroup of  .
.
 , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of  as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
 of dimension
of dimension  is
is 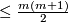 (the dimension of
(the dimension of 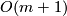 , which acts on
, which acts on 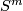 ), and if the degree of symmetry is
), and if the degree of symmetry is 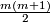 then
then  is diffeomorphic to
is diffeomorphic to 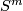 or
or 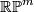 .
.
 , such that the multiplication
, such that the multiplication 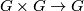 and the attaching of an inverse
and the attaching of an inverse 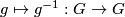 are smooth maps.
A morphism between two Lie groups
are smooth maps.
A morphism between two Lie groups  and
and  is a map
is a map 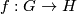 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 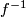 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
.