Lie groups I: Definition and examples
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 Introduction
This is part I of a series of articles about Lie groups. We define Lie groups and homomorphisms and give the most important examples. In following pages of this series we define the fundamental invariants like the Dynkin diagram, and report about the classification of compact Lie groups. We also report about exceptional Lie groups.
[edit] 2 Definition and examples
Definition 2.1. A Lie group is a finite dimensional smooth manifold  together with a group structure on
together with a group structure on  , such that the multiplication
, such that the multiplication 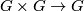 and the attaching of an inverse
and the attaching of an inverse 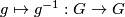 are smooth maps.
are smooth maps.
 and
and  is a map
is a map 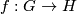 , which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map
, which at the same time is smooth and a group homomorphism. An isomorphism is a bijective map  such that
such that  and
and 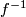 are morphisms. A Lie subgroup is a subgroup
are morphisms. A Lie subgroup is a subgroup  in
in  such that
such that  is also a smooth submanifold of
is also a smooth submanifold of  .
.It is enough to require that the multiplication is smooth, the smoothness of the inverse map can be derived from this. Obviously the product of two Lie groups or a finite sequence of Lie groups is a Lie group.
The simplest examples of Lie groups are countable groups, which with the discrete topology are a  -dimensional Lie group. In particular all finite groups are
-dimensional Lie group. In particular all finite groups are  -dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over
-dimensional Lie groups. The most basic Lie groups of positive dimension are matrix groups. The general linear groups over  ,
, 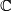 or the quternions
or the quternions  :
:

They are smooth manifolds as open subsets of the vector space of all corresponding matrices. Their dimension is 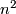 ,
, 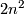 and
and 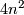 resp. (note that Lie groups are real manifolds, this explains the formula for the dimension).
resp. (note that Lie groups are real manifolds, this explains the formula for the dimension). 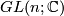 is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
is also a complex manifold and one obtains a complex Lie group but we will here only consider real Lie groups.
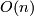 , the orthogonal group, the hermitian matrices
, the orthogonal group, the hermitian matrices 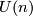 , the unitary group, and the symplectic matrices
, the unitary group, and the symplectic matrices 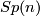 , the symplectic group. The way to see this is to consider the map
, the symplectic group. The way to see this is to consider the map 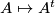 from
from 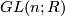 to the vector space of symmetric matrices and to show that the unit matrix
to the vector space of symmetric matrices and to show that the unit matrix  is a regular value. Thus the preimage of
is a regular value. Thus the preimage of  , which is
, which is 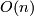 is a smooth submanifold and so
is a smooth submanifold and so 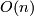 is a Lie submanifold of
is a Lie submanifold of 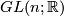 . Similarly one considers the map
. Similarly one considers the map 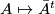 from
from 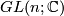 to the skew symmetric matrices over
to the skew symmetric matrices over 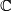 and shows again that
and shows again that  is a regular value. The dimension of
is a regular value. The dimension of 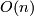 is
is 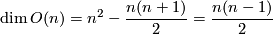
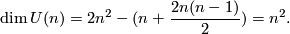
By definition these subgroups are closed subgroups. Since they are bounded subspaces of the vector space of all matrices they are compact. They contain the Lie subgroups of all matrices with determinant  , the special orthogonal group or special unitary group:
, the special orthogonal group or special unitary group:
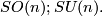
The first is just the component of  in
in 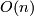 , whereas the second is the preimage of the regular value
, whereas the second is the preimage of the regular value  in
in  and so has codimension
and so has codimension  , implying:
, implying:
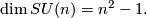
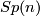 is not the group of isometries of a non-degenerate skew-symmetric
is not the group of isometries of a non-degenerate skew-symmetric  -bilinear form, but the group of the hermitian form on
-bilinear form, but the group of the hermitian form on 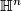
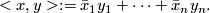
With this definition one proceeds as in the examples above and show that 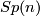 is a Lie group of dimension
is a Lie group of dimension
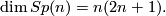
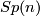 is
is  , thus we don't consider the groups
, thus we don't consider the groups 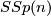 .
.
As mentioned above 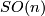 is the component of
is the component of  in
in 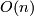 . For
. For 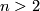 it's fundamental group is
it's fundamental group is 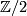 [???] generated by the inclusion
[???] generated by the inclusion 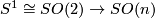 . If
. If  is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of
is a Lie group then by construction of the universal covering this is a Lie group again. In particular the universal covering of 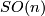 for
for 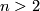 is a Lie group denoted by
is a Lie group denoted by 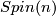 , the Spinor group. There is a more explicit construction of
, the Spinor group. There is a more explicit construction of 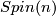 in terms of Clifford algebras [???].
in terms of Clifford algebras [???].
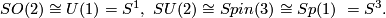
A special role in the world of Lie groups play the tori, the Lie groups
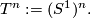
Here are a few fundamental examples of non-compact Lie groups:
1.) The Lorentz group 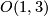 the group of the isometries of the Minkowski space, the isometries of the form on
the group of the isometries of the Minkowski space, the isometries of the form on 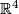 given by
given by 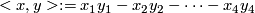 . It's dimension is
. It's dimension is  .
.
2.) The Heisenberg Group  consisting of upper
consisting of upper 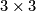 matrices with diagonal entries
matrices with diagonal entries  . It's dimension is
. It's dimension is  .
.
The following theorems give a rough picture of all Lie groups:
Theorem 2.2. A compact Lie group  is isomorphic to a Lie subgroup of
is isomorphic to a Lie subgroup of 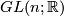 for some
for some  [???].
[???].
Theorem 2.3. A subgroup of a Lie group is a Lie subgroup, if and only if it is closed as a topological subspace [???].
Thus it's easy to test, whether a subgroup of a Lie group is a Lie subgroup.
[edit] Further discussion
Why are Lie groups interesting? There are many different answers to this question. Probably everybody will agree that Lie groups, in particular compact Lie groups, give the mathematical language for defining and studying symmetries. Given a geometric object, say a closed smooth manifold  with a Riemannian metric
with a Riemannian metric  , then one can consider the group of self isometries
, then one can consider the group of self isometries 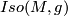 . By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map
. By a theorem of Myers and Steenrod \cite {???} this is a compact Lie group in such a way that the map 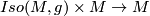 mapping
mapping 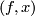 to
to 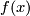 is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of
is a smooth map [Kobayashi transformation groups ...]. Thus we have a smooth action of 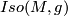 on
on  . The size of this group is a measure for the symmetry of
. The size of this group is a measure for the symmetry of 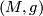 . In turn if a compact Lie group
. In turn if a compact Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , then there is a Riemannian metric on
, then there is a Riemannian metric on  such that
such that  acts by isometries (choose an arbitrary Riemannian metric and average it over
acts by isometries (choose an arbitrary Riemannian metric and average it over  using a Haar measure). If the action is effective (meaning that if
using a Haar measure). If the action is effective (meaning that if  acts trivially, the
acts trivially, the 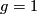 ), then
), then  is a subgroup of
is a subgroup of 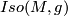 .
.
Motivated by these considerations one defines an invariant for closed smooth manifolds , the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on
, the degree of symmetry which is the largest dimension of a compact Lie group acting effectively on  (or equivalently the largest dimension of
(or equivalently the largest dimension of 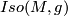 as
as  varies over all Riemannian metrics of
varies over all Riemannian metrics of  ). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
). The following result distinguishes the spheres and real projective spaces from all other manifolds as the most symmetric ones:
Theorem [Frobenius-Birkhoff] 4.1. The degree of symmetry of a clsoed manifold  of dimension
of dimension  is
is 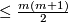 (the dimension of
(the dimension of 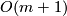 , which acts on
, which acts on 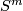 ), and if the degree of symmetry is
), and if the degree of symmetry is 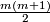 then
then  is diffeomorphic to
is diffeomorphic to 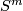 or
or 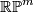 .
.