Knots, i.e. embeddings of spheres
(Created page with "(I would suggest including the classification of simple knots a la Kearton et. al. in this section.---John Klein)") |
Askopenkov (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | {{Stub}} | ||
| + | For notation and conventions throughout this page see [[High_codimension_embeddings|high codimension embeddings]]. | ||
| + | == Examples == | ||
| + | |||
| + | === The Haefliger trefoil knot === | ||
| + | <wikitex>; | ||
| + | Let us construct a smooth embedding $t:S^3\to\Rr^6$ (which is a generator of $E^6_D(S^3)\cong\Zz$) \cite{Haefliger1962}, 4.1. A miraculous property of this embedding is that it is not ''smoothly'' isotopic to the standard embedding, but is ''piecewise smoothly'' isotopic to the standard embedding. | ||
| + | |||
| + | Denote coordinates in $\Rr^6$ by $(x,y,z)=(x_1,x_2,y_1,y_2,z_1,z_2)$. The higher-dimensional trefoil knot $t$ is obtained by joining with two tubes the higher-dimensional ''Borromean rings'', i.e. the three spheres given by the following three systems of equations: | ||
| + | $$\left\{\begin{array}{c} x=0\\ |y|^2+2|z|^2=1\end{array}\right., \qquad | ||
| + | \left\{\begin{array}{c} y=0\\ |z|^2+2|x|^2=1\end{array}\right. \qquad\text{and}\qquad \left\{\begin{array}{c} z=0\\ |x|^2+2|y|^2=1 \end{array}\right..$$ | ||
| + | See Figures 3.5 and 3.6 of \cite{Skopenkov2006}. | ||
| + | |||
| + | Analogously for $k>1$ one constructs a smooth embedding $t:S^{2k-1}\to\Rr^{3k}$ (which is a generator of $E_D^{3k}(S^3)\cong\Zz_{(k)}$) that is not ''smoothly'' isotopic to the standard embedding, but is ''piecewise smoothly'' isotopic to it \cite{Haefliger1962}. | ||
| + | </wikitex> | ||
| + | |||
| + | === Classification === | ||
| + | |||
(I would suggest including the classification of simple knots a la Kearton et. al. in this section.---John Klein) | (I would suggest including the classification of simple knots a la Kearton et. al. in this section.---John Klein) | ||
Revision as of 09:44, 26 April 2016
|
This page has not been refereed. The information given here might be incomplete or provisional. |
For notation and conventions throughout this page see high codimension embeddings.
1 Examples
1.1 The Haefliger trefoil knot
Let us construct a smooth embedding 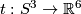 (which is a generator of
(which is a generator of 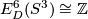 ) [Haefliger1962], 4.1. A miraculous property of this embedding is that it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to the standard embedding.
) [Haefliger1962], 4.1. A miraculous property of this embedding is that it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to the standard embedding.
Denote coordinates in  by
by 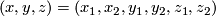 . The higher-dimensional trefoil knot
. The higher-dimensional trefoil knot  is obtained by joining with two tubes the higher-dimensional Borromean rings, i.e. the three spheres given by the following three systems of equations:
is obtained by joining with two tubes the higher-dimensional Borromean rings, i.e. the three spheres given by the following three systems of equations:
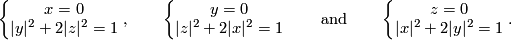
See Figures 3.5 and 3.6 of [Skopenkov2006].
Analogously for  one constructs a smooth embedding
one constructs a smooth embedding 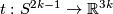 (which is a generator of
(which is a generator of 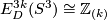 ) that is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
) that is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
1.2 Classification
(I would suggest including the classification of simple knots a la Kearton et. al. in this section.---John Klein)