Kappa classes (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; Let $i \colon SG \to G/TOP$ be the canonical map and let $\kappa_{4k-2} \in H^{4k-2}(G/PL; \Zz/2)$ be defined as in \cite{Madsen&Milgram1979|Theorem 4.9}. In addit...") |
m |
||
| Line 9: | Line 9: | ||
# Show that there is a framed manifold of Kervaire invariant one in dimension $(4k-2)$ if and only if there is a closed framed $(4k-2)$-manifold $M$ and a map $\varphi \colon M \to SG$ such that $\phi^*(\kappa_{4k-2}) \in H^{4k-2}(M; \Zz/2)$ is a generator. | # Show that there is a framed manifold of Kervaire invariant one in dimension $(4k-2)$ if and only if there is a closed framed $(4k-2)$-manifold $M$ and a map $\varphi \colon M \to SG$ such that $\phi^*(\kappa_{4k-2}) \in H^{4k-2}(M; \Zz/2)$ is a generator. | ||
{{endthm}} | {{endthm}} | ||
| − | |||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
Latest revision as of 01:17, 26 August 2013
Let 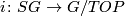 be the canonical map and let
be the canonical map and let 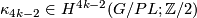 be
defined as in [Madsen&Milgram1979, Theorem 4.9]. In addition let
be
defined as in [Madsen&Milgram1979, Theorem 4.9]. In addition let 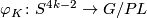 be the normal invariant of a degree one normal map
be the normal invariant of a degree one normal map 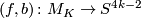 from the Kervaire manifold
to the
from the Kervaire manifold
to the 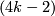 -sphere.
-sphere.
Exercise 0.1.
- Show that
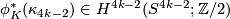 is the generator.
is the generator.
- Show that there is a framed manifold of Kervaire invariant one in dimension
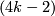 if and only if there is a map
if and only if there is a map 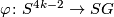 such that
such that 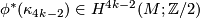 is a generator.
is a generator.
- Show that there is a framed manifold of Kervaire invariant one in dimension
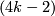 if and only if there is a closed framed
if and only if there is a closed framed 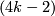 -manifold
-manifold  and a map
and a map 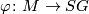 such that
such that 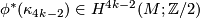 is a generator.
is a generator.
[edit] References
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002