Intersection form
| Line 41: | Line 41: | ||
The form $q$ may have two different ''types''. It is of type ''even'' if $q(x,x)$ is an even number for any element $x$. Equivalently, if $q$ is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise, $q$ is said of type ''odd''. | The form $q$ may have two different ''types''. It is of type ''even'' if $q(x,x)$ is an even number for any element $x$. Equivalently, if $q$ is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise, $q$ is said of type ''odd''. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</wikitex> | </wikitex> | ||
| Line 53: | Line 48: | ||
{{beginthm|Theorem|(Serre?)}} Two indefinite unimodular symmetric bilinear forms $q, q'$ over $\mathbb{Z}$ are equivalent if and only if $q$ and $q'$ have the same rank, signature and type. {{endthm}} | {{beginthm|Theorem|(Serre?)}} Two indefinite unimodular symmetric bilinear forms $q, q'$ over $\mathbb{Z}$ are equivalent if and only if $q$ and $q'$ have the same rank, signature and type. {{endthm}} | ||
| − | |||
| − | == Examples == | + | |
| + | There is a further invariant of a unimodular symmetric bilinear form $q$ on $V$: An element $c \in V$ is called a ''characteristic vector'' of the form if one has | ||
| + | $$ | ||
| + | q(c,x) \equiv q(x,x) \ (\text{mod} \ 2) | ||
| + | $$ | ||
| + | for all elements $x \in V$. Characteristic vectors always exist. In fact, when reduced modulo 2, the map $x \mapsto q(x,x) \in \mathbb{Z}/2$ is linear. By unimodularity there therefore exists an element $c$ such that the map $q(c,-)$ equals this linear map. | ||
| + | |||
| + | The form $q$ is even if and only if $0$ is a characteristic vector. | ||
| + | If $c$ and $c'$ are characteristic vectors for $q$, then there is an element $h$ with $c' = c + 2h$. This follows from unimodularity. As a consequence, the number $q(c,c)$ is independent of the chosen characteristic vector $c$ modulo 8. One can be more specific: | ||
| + | |||
| + | {{beginthm|Proposition|}} | ||
| + | For a characteristic vector $c$ of the unimodular symmetric bilinear form $q$ one has | ||
| + | $$ | ||
| + | q(c,c) \equiv \text{sign}(q) \ (\text{mod} \ 8) | ||
| + | $$ | ||
| + | |||
| + | {{endthm}} | ||
| + | Proof: | ||
| + | |||
| + | </wikitex> | ||
| + | == Examples, Realisations of indefinite forms == | ||
<wikitex>; | <wikitex>; | ||
Revision as of 16:15, 7 June 2010
Contents |
1 Introduction
For a closed (topological or smooth) manifold  of dimension
of dimension 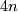 the intersection form
the intersection form
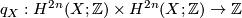
is obtained by the formula
![\displaystyle q_X(x,y) = \langle x \smile y , [X] \rangle ,](/images/math/f/5/7/f57e1e8038d92f22b87cb9c7943813d8.png)
i.e. the cup product of  and
and  is evaluated on the fundamental cycle given by the manifold
is evaluated on the fundamental cycle given by the manifold  .
.
 descends to a bilinear pairing on the free module
descends to a bilinear pairing on the free module 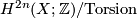 . It is a symmetric and unimodular (in particular non-degenerate) pairing, the latter follows from Poincaré duality.
. It is a symmetric and unimodular (in particular non-degenerate) pairing, the latter follows from Poincaré duality.
2 Algebraic invariants
Let  and
and 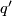 be unimodular symmetric bilinear forms on underlying free
be unimodular symmetric bilinear forms on underlying free  -modules
-modules  and
and 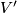 respectively. The two forms
respectively. The two forms  and
and 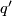 are said equivalent if there is an isomorphism
are said equivalent if there is an isomorphism 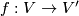 such that
such that 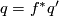 .
.
A form  is called definite if it is positive or negative definite, otherwise it is called indefinite.
The rank of q is the rank of the underlying
is called definite if it is positive or negative definite, otherwise it is called indefinite.
The rank of q is the rank of the underlying  -module V.
-module V.
As  is symmetric it is diagonalisable over the real numbers. If
is symmetric it is diagonalisable over the real numbers. If 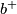 denotes the dimension of a maximal subspace on which the form is positive definite, and if
denotes the dimension of a maximal subspace on which the form is positive definite, and if 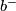 is the dimension of a maximal subspace on which the form is negative definite, then the signature of
is the dimension of a maximal subspace on which the form is negative definite, then the signature of  is defined to be
is defined to be
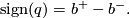
The form  may have two different types. It is of type even if
may have two different types. It is of type even if 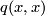 is an even number for any element
is an even number for any element  . Equivalently, if
. Equivalently, if  is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,
is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,  is said of type odd.
is said of type odd.
3 Classification of indefinite forms
There is a simple classification result of indefinite forms:
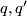 over
over  are equivalent if and only if
are equivalent if and only if  and
and 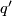 have the same rank, signature and type.
have the same rank, signature and type.
There is a further invariant of a unimodular symmetric bilinear form  on
on  : An element
: An element 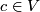 is called a characteristic vector of the form if one has
is called a characteristic vector of the form if one has
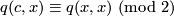
for all elements 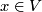 . Characteristic vectors always exist. In fact, when reduced modulo 2, the map
. Characteristic vectors always exist. In fact, when reduced modulo 2, the map 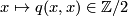 is linear. By unimodularity there therefore exists an element
is linear. By unimodularity there therefore exists an element  such that the map
such that the map 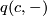 equals this linear map.
equals this linear map.
The form  is even if and only if
is even if and only if  is a characteristic vector.
If
is a characteristic vector.
If  and
and 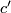 are characteristic vectors for
are characteristic vectors for  , then there is an element
, then there is an element  with
with 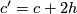 . This follows from unimodularity. As a consequence, the number
. This follows from unimodularity. As a consequence, the number 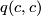 is independent of the chosen characteristic vector
is independent of the chosen characteristic vector  modulo 8. One can be more specific:
modulo 8. One can be more specific:
Proposition 3.2.
For a characteristic vector  of the unimodular symmetric bilinear form
of the unimodular symmetric bilinear form  one has
one has
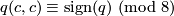
Proof:
4 Examples, Realisations of indefinite forms
5 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |
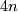 the intersection form
the intersection form
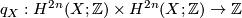
is obtained by the formula
![\displaystyle q_X(x,y) = \langle x \smile y , [X] \rangle ,](/images/math/f/5/7/f57e1e8038d92f22b87cb9c7943813d8.png)
i.e. the cup product of  and
and  is evaluated on the fundamental cycle given by the manifold
is evaluated on the fundamental cycle given by the manifold  .
.
 descends to a bilinear pairing on the free module
descends to a bilinear pairing on the free module 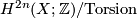 . It is a symmetric and unimodular (in particular non-degenerate) pairing, the latter follows from Poincaré duality.
. It is a symmetric and unimodular (in particular non-degenerate) pairing, the latter follows from Poincaré duality.
2 Algebraic invariants
Let  and
and 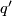 be unimodular symmetric bilinear forms on underlying free
be unimodular symmetric bilinear forms on underlying free  -modules
-modules  and
and 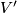 respectively. The two forms
respectively. The two forms  and
and 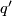 are said equivalent if there is an isomorphism
are said equivalent if there is an isomorphism 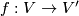 such that
such that 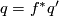 .
.
A form  is called definite if it is positive or negative definite, otherwise it is called indefinite.
The rank of q is the rank of the underlying
is called definite if it is positive or negative definite, otherwise it is called indefinite.
The rank of q is the rank of the underlying  -module V.
-module V.
As  is symmetric it is diagonalisable over the real numbers. If
is symmetric it is diagonalisable over the real numbers. If 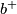 denotes the dimension of a maximal subspace on which the form is positive definite, and if
denotes the dimension of a maximal subspace on which the form is positive definite, and if 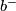 is the dimension of a maximal subspace on which the form is negative definite, then the signature of
is the dimension of a maximal subspace on which the form is negative definite, then the signature of  is defined to be
is defined to be
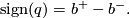
The form  may have two different types. It is of type even if
may have two different types. It is of type even if 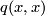 is an even number for any element
is an even number for any element  . Equivalently, if
. Equivalently, if  is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,
is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,  is said of type odd.
is said of type odd.
3 Classification of indefinite forms
There is a simple classification result of indefinite forms:
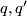 over
over  are equivalent if and only if
are equivalent if and only if  and
and 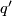 have the same rank, signature and type.
have the same rank, signature and type.
There is a further invariant of a unimodular symmetric bilinear form  on
on  : An element
: An element 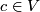 is called a characteristic vector of the form if one has
is called a characteristic vector of the form if one has
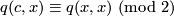
for all elements 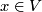 . Characteristic vectors always exist. In fact, when reduced modulo 2, the map
. Characteristic vectors always exist. In fact, when reduced modulo 2, the map 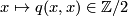 is linear. By unimodularity there therefore exists an element
is linear. By unimodularity there therefore exists an element  such that the map
such that the map 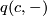 equals this linear map.
equals this linear map.
The form  is even if and only if
is even if and only if  is a characteristic vector.
If
is a characteristic vector.
If  and
and 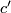 are characteristic vectors for
are characteristic vectors for  , then there is an element
, then there is an element  with
with 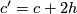 . This follows from unimodularity. As a consequence, the number
. This follows from unimodularity. As a consequence, the number 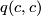 is independent of the chosen characteristic vector
is independent of the chosen characteristic vector  modulo 8. One can be more specific:
modulo 8. One can be more specific:
Proposition 3.2.
For a characteristic vector  of the unimodular symmetric bilinear form
of the unimodular symmetric bilinear form  one has
one has
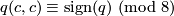
Proof:
4 Examples, Realisations of indefinite forms
5 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |