Inertia group II (Ex)
(Difference between revisions)
m |
m |
||
| Line 6: | Line 6: | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
# Show that $\Sigma \in I_H(M)$ if and only if ${\rm Id}_M \colon \Sigma \sharp M \to M$ is equivalent to ${\rm Id}_M \colon M \to M$ in $\mathcal{S}(M)$. | # Show that $\Sigma \in I_H(M)$ if and only if ${\rm Id}_M \colon \Sigma \sharp M \to M$ is equivalent to ${\rm Id}_M \colon M \to M$ in $\mathcal{S}(M)$. | ||
| − | # Determine $ | + | # Determine $I_H(\Hh P^2)$. |
| + | # Assuming that $I(\Hh P^2) = \Theta_8$, deduce that $\Hh P^2$ admits a self-homotopy equivalence which is not homotopic to a diffeomorphism. | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Revision as of 23:44, 27 August 2013
Let  be a closed smooth oriented
be a closed smooth oriented  -manifold. The homotopy inertia group of
-manifold. The homotopy inertia group of  ,
, 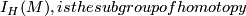 n
n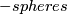 \Theta_n$ defined by
\Theta_n$ defined by
Tex syntax error
Tex syntax errorwe regard
 and
and 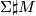 as the same topological space (with different smooth structures).
as the same topological space (with different smooth structures).
Exercise 0.1.
- Show that
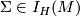 if and only if
if and only if Tex syntax error
is equivalent toTex syntax error
in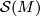 .
.
- Determine
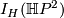 .
.
- Assuming that
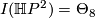 , deduce that
, deduce that 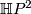 admits a self-homotopy equivalence which is not homotopic to a diffeomorphism.
admits a self-homotopy equivalence which is not homotopic to a diffeomorphism.