Talk:Inertia group II (Ex)
1. 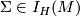 iff
iff 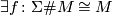 with
with 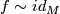 , iff the following diagram commutes up to homotopy:
, iff the following diagram commutes up to homotopy:
![\xymatrix{ &\Sigma\# M \ar[r]^-{id_M} \ar[d]^-{f} & M \\ &M \ar[ru]_-{id_M}}](/images/math/9/7/b/97b5279b415f42473f266a1a93e18840.png)
2. 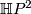 fits into the cofibration sequence
fits into the cofibration sequence ![\xymatrix{S^4 \ar[r] &\Hh P^2 \ar[r]^-{c} &S^8 }](/images/math/e/f/0/ef0a952f9357750e8c785ad7dbafcb5c.png) where
where  is the collapse map of the
is the collapse map of the  -skeleton. Then the Puppe exact sequence of the cohomology theory represented by
-skeleton. Then the Puppe exact sequence of the cohomology theory represented by 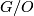 gives an exact sequence
gives an exact sequence
![\xymatrix{\pi_5(G/O) \ar[r] & \pi_8 (G/O) \ar[r]^-{c^*} &[\Hh P^2, G/O]\ar[r] & \pi_4(G/O).}](/images/math/5/e/c/5ecdec2fafe5cfad67c4673896d57bad.png)
It is known that 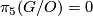 , and so
, and so 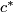 is injective. From the surgery exact sequences of
is injective. From the surgery exact sequences of 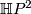 and
and 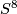 we get the following commutative diagram (see for example [Crowley2010, Lemma 3.4]):
we get the following commutative diagram (see for example [Crowley2010, Lemma 3.4]):
![\xymatrix{&0 \ar[r]\ar[rd] &\Theta_8 \ar[r]^-{\eta} \ar[d]^-{a} &\pi_8(G/O) \ar[r] \ar[d]^-{c^*} &\Zz \\ & & \mathcal{S}(\Hh P^2) \ar[r]^-{\tilde{\eta}} &[\Hh P^2, G/O] \ar[ru]}](/images/math/1/8/5/1857219978a1cd62fe08f0ff5d17860c.png)
Here we are using the facts that 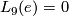 ,
, 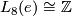 and
and 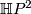 is simply connected. Injectivity of
is simply connected. Injectivity of 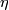 and
and 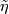 follow from the diagram, and combine with the injectivity of
follow from the diagram, and combine with the injectivity of 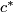 to show that
to show that  is injective. But by part 1
is injective. But by part 1 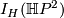 is exactly the kernel of
is exactly the kernel of  , and so
, and so 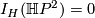 .
.
3. Let  be the non-zero element of
be the non-zero element of 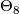 , and let
, and let 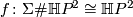 be a diffeomorphism. Then
be a diffeomorphism. Then 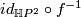 is a homotopy self-equivalence. Suppose this composition is homotopic to a diffeomorphism
is a homotopy self-equivalence. Suppose this composition is homotopic to a diffeomorphism  . Then the following diagram would commute up to homotopy:
. Then the following diagram would commute up to homotopy:
![\xymatrix{ &\Sigma\# \Hh P^2 \ar[r]^-{id_{\Hh P^2}} \ar[d]^-{f} & \Hh P^2 \\ &\Hh P^2 \ar[ur]_-{\phi} }](/images/math/9/d/e/9de412d05026837b5dd1d6e3259b8932.png)
In other words,  is a diffeomorphism homotopic to
is a diffeomorphism homotopic to 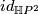 . Therefore
. Therefore  would be an element of
would be an element of 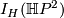 , which is a contradiction.
, which is a contradiction.
Note that this proof generalizes to show: If  is a manifold such that
is a manifold such that 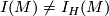 , then
, then  admits a homotopy self-equivalence which is not homotopic to the identity.
admits a homotopy self-equivalence which is not homotopic to the identity.
[edit] References
- [Crowley2010] D. Crowley, The smooth structure set of
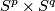 , Geom. Dedicata 148 (2010), 15–33. MR2721618 (2012a:57041) Zbl 1207.57043
, Geom. Dedicata 148 (2010), 15–33. MR2721618 (2012a:57041) Zbl 1207.57043