Hirzebruch surfaces
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:48, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
Contents |
1 Introduction
Hirzebruch surfaces were introduced by Hirzebruch (without that name) in his thesis [Hirzebruch1953a]. They are algebraic surfaces over the complex numbers. Here we consider them as smooth manifolds. The interest in them comes from Hirzebruch's result that as complex manifolds they are pairwise distinct whereas there are only two diffeomorphism types.
2 Construction and examples
Let ![L:= \{[x],y)\in \mathbb {CP}^1 \times \mathbb C^2 |y = \lambda x](/images/math/8/8/d/88df819a4f4cb39ea67b3a4edf99397a.png) for some
for some 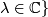 be the tautological line bundle over
be the tautological line bundle over 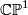 . Recall that if
. Recall that if  is a vector bundle over
is a vector bundle over  (real or complex) taking fibrewise the projective space yields a bundle
(real or complex) taking fibrewise the projective space yields a bundle 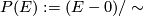 , where
, where 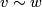 if and only if there is a
if and only if there is a  in the ground field such that
in the ground field such that 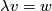 , with fibres P(E_x), the associated projective bundle. If
, with fibres P(E_x), the associated projective bundle. If  is a smooth vector bundle over a smooth manifold, then P(E) is a smooth manifold, or similarly if
is a smooth vector bundle over a smooth manifold, then P(E) is a smooth manifold, or similarly if  and
and  are holomorphic, the total space is a complex manifold.
are holomorphic, the total space is a complex manifold.
For 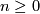 define
define  as
as 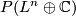 , where
, where 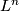 is the tensor product of
is the tensor product of  copies of
copies of  with itself. For
with itself. For 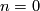 the bundle
the bundle 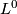 is by definition the trivial bundle. For
is by definition the trivial bundle. For  we define
we define  as the corresponding construction with
as the corresponding construction with 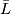 , the complex conjugated bundle, instead of
, the complex conjugated bundle, instead of  . These are the
. These are the 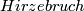
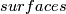 . They come with a complex structure but we consider them as smooth manifolds.
. They come with a complex structure but we consider them as smooth manifolds.
3 Invariants
The dimension as a smooth manifold is  .
.
Since the Hirzebruch surfaces are - as real manifold -  -bundles over
-bundles over  they are closed and - by the orientation coming from the complex structure - oriented
they are closed and - by the orientation coming from the complex structure - oriented  -dimensional manifolds and the homotopy sequence of a fibration implies that they are simply connected.
-dimensional manifolds and the homotopy sequence of a fibration implies that they are simply connected.
The signature of  is zero since the Hirzebruch surfaces are the boundary of the associated
is zero since the Hirzebruch surfaces are the boundary of the associated 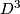 -bundle (or derive this directly from the intersection form below).
-bundle (or derive this directly from the intersection form below).
The homology is trivial except in degree  and
and  , where it is
, where it is  and in degree
and in degree  where it is isomorphic to
where it is isomorphic to 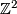 with basis given by the homology class represented by a fibre and the homology class of the base considered as homology class of
with basis given by the homology class represented by a fibre and the homology class of the base considered as homology class of  using the section of points at infinity.
using the section of points at infinity.
The intersection form on 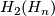 is with respect to this basis given by the matrix
is with respect to this basis given by the matrix
0 1
1 -n
Here we use that tht the self intersection number of a class represented by an embedded oriented submanifold is the evaluation of the Euler class of the normal bundle on the fundamental class.
The Euler characteristic is 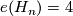 .
.
The first Pontrjagin class of  is zero (its evaluation on the fundamental class is a bordism invariant) and the second Stiefel-Whitney class
is zero (its evaluation on the fundamental class is a bordism invariant) and the second Stiefel-Whitney class 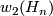 evaluates trivial on the first base element and by
evaluates trivial on the first base element and by  mod
mod  on the second. In particular
on the second. In particular  is a Spin-manifold if and only if
is a Spin-manifold if and only if  is even. If we consider them as complex manifolds then we have the first Chern class
is even. If we consider them as complex manifolds then we have the first Chern class 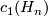 , which evaluates trivial on the first base element and by
, which evaluates trivial on the first base element and by 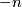 on the second.
on the second.
4 Classification
The intersection form implies that if  is diffeomorphic to
is diffeomorphic to 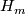 , then
, then  mod
mod  . On the other hand they are - as smooth manifolds - total spaces of the sphere bundle of a
. On the other hand they are - as smooth manifolds - total spaces of the sphere bundle of a  -dimensional vector bundle over
-dimensional vector bundle over  . these bundles are classified by
. these bundles are classified by 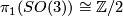 (note that
(note that  is diffeomorphic to
is diffeomorphic to 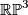 ). Thus there are at most two diffeomorphism types of the fibre and so we conclude:
). Thus there are at most two diffeomorphism types of the fibre and so we conclude:
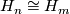
if and only if  mod
mod  , where
, where 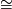 means diffeomorphic. By construction
means diffeomorphic. By construction 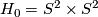 and by an easy consideration
and by an easy consideration 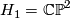 #
# 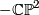 , where # is the connected sum and
, where # is the connected sum and 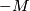 is
is  with the opposite orientation.
with the opposite orientation.
For more information on Hirzebruch surfaces, in particular why they are pairwise distinct as complex manifolds, see [Hirzebruch1953a].
5 Further remarks
The Hirzebruch surfaces are the first stage of the so called Bott tower, which is inductively constructed starting from a point as the total space of a projective bundle associated to  , where
, where  is a line bundle over a lower Bott tower (for more details see Masuda). The classification of the Bott manifolds up to homeomorphism or diffeomorphism is an interesting open problem. In particular one can ask wether the integral cohomology ring determines the homeomorphism or diffeomorphism type.
is a line bundle over a lower Bott tower (for more details see Masuda). The classification of the Bott manifolds up to homeomorphism or diffeomorphism is an interesting open problem. In particular one can ask wether the integral cohomology ring determines the homeomorphism or diffeomorphism type.
6 References
- [Hirzebruch1953a] F. Hirzebruch, On Steenrod's reduced powers, the index of inertia, and the Todd genus, Proc. Nat. Acad. Sci. U. S. A. 39 (1953), 951–956. MR0063670 (16,159f) Zbl 0051.14501
Please modify these headings or choose other headings according to your needs.
|
This page has not been refereed. The information given here might be incomplete or provisional. |
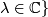 be the tautological line bundle over
be the tautological line bundle over 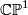 . Recall that if
. Recall that if  is a vector bundle over
is a vector bundle over  (real or complex) taking fibrewise the projective space yields a bundle
(real or complex) taking fibrewise the projective space yields a bundle 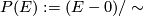 , where
, where 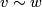 if and only if there is a
if and only if there is a  in the ground field such that
in the ground field such that 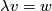 , with fibres P(E_x), the associated projective bundle. If
, with fibres P(E_x), the associated projective bundle. If  is a smooth vector bundle over a smooth manifold, then P(E) is a smooth manifold, or similarly if
is a smooth vector bundle over a smooth manifold, then P(E) is a smooth manifold, or similarly if  and
and  are holomorphic, the total space is a complex manifold.
are holomorphic, the total space is a complex manifold.
For 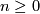 define
define  as
as 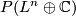 , where
, where 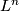 is the tensor product of
is the tensor product of  copies of
copies of  with itself. For
with itself. For 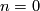 the bundle
the bundle 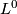 is by definition the trivial bundle. For
is by definition the trivial bundle. For  we define
we define  as the corresponding construction with
as the corresponding construction with 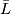 , the complex conjugated bundle, instead of
, the complex conjugated bundle, instead of  . These are the
. These are the 
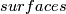 . They come with a complex structure but we consider them as smooth manifolds.
. They come with a complex structure but we consider them as smooth manifolds.
3 Invariants
The dimension as a smooth manifold is  .
.
Since the Hirzebruch surfaces are - as real manifold -  -bundles over
-bundles over  they are closed and - by the orientation coming from the complex structure - oriented
they are closed and - by the orientation coming from the complex structure - oriented  -dimensional manifolds and the homotopy sequence of a fibration implies that they are simply connected.
-dimensional manifolds and the homotopy sequence of a fibration implies that they are simply connected.
The signature of  is zero since the Hirzebruch surfaces are the boundary of the associated
is zero since the Hirzebruch surfaces are the boundary of the associated 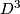 -bundle (or derive this directly from the intersection form below).
-bundle (or derive this directly from the intersection form below).
The homology is trivial except in degree  and
and  , where it is
, where it is  and in degree
and in degree  where it is isomorphic to
where it is isomorphic to 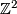 with basis given by the homology class represented by a fibre and the homology class of the base considered as homology class of
with basis given by the homology class represented by a fibre and the homology class of the base considered as homology class of  using the section of points at infinity.
using the section of points at infinity.
The intersection form on 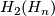 is with respect to this basis given by the matrix
is with respect to this basis given by the matrix
0 1
1 -n
Here we use that tht the self intersection number of a class represented by an embedded oriented submanifold is the evaluation of the Euler class of the normal bundle on the fundamental class.
The Euler characteristic is 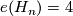 .
.
The first Pontrjagin class of  is zero (its evaluation on the fundamental class is a bordism invariant) and the second Stiefel-Whitney class
is zero (its evaluation on the fundamental class is a bordism invariant) and the second Stiefel-Whitney class 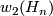 evaluates trivial on the first base element and by
evaluates trivial on the first base element and by  mod
mod  on the second. In particular
on the second. In particular  is a Spin-manifold if and only if
is a Spin-manifold if and only if  is even. If we consider them as complex manifolds then we have the first Chern class
is even. If we consider them as complex manifolds then we have the first Chern class 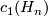 , which evaluates trivial on the first base element and by
, which evaluates trivial on the first base element and by 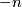 on the second.
on the second.
4 Classification
The intersection form implies that if  is diffeomorphic to
is diffeomorphic to 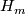 , then
, then  mod
mod  . On the other hand they are - as smooth manifolds - total spaces of the sphere bundle of a
. On the other hand they are - as smooth manifolds - total spaces of the sphere bundle of a  -dimensional vector bundle over
-dimensional vector bundle over  . these bundles are classified by
. these bundles are classified by 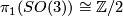 (note that
(note that  is diffeomorphic to
is diffeomorphic to 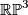 ). Thus there are at most two diffeomorphism types of the fibre and so we conclude:
). Thus there are at most two diffeomorphism types of the fibre and so we conclude:
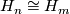
if and only if  mod
mod  , where
, where 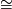 means diffeomorphic. By construction
means diffeomorphic. By construction 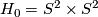 and by an easy consideration
and by an easy consideration 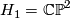 #
# 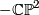 , where # is the connected sum and
, where # is the connected sum and 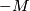 is
is  with the opposite orientation.
with the opposite orientation.
For more information on Hirzebruch surfaces, in particular why they are pairwise distinct as complex manifolds, see [Hirzebruch1953a].
5 Further remarks
The Hirzebruch surfaces are the first stage of the so called Bott tower, which is inductively constructed starting from a point as the total space of a projective bundle associated to  , where
, where  is a line bundle over a lower Bott tower (for more details see Masuda). The classification of the Bott manifolds up to homeomorphism or diffeomorphism is an interesting open problem. In particular one can ask wether the integral cohomology ring determines the homeomorphism or diffeomorphism type.
is a line bundle over a lower Bott tower (for more details see Masuda). The classification of the Bott manifolds up to homeomorphism or diffeomorphism is an interesting open problem. In particular one can ask wether the integral cohomology ring determines the homeomorphism or diffeomorphism type.
6 References
- [Hirzebruch1953a] F. Hirzebruch, On Steenrod's reduced powers, the index of inertia, and the Todd genus, Proc. Nat. Acad. Sci. U. S. A. 39 (1953), 951–956. MR0063670 (16,159f) Zbl 0051.14501
Please modify these headings or choose other headings according to your needs.
|
This page has not been refereed. The information given here might be incomplete or provisional. |