High codimension links
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
For notation and conventions throughout this page see high codimension embeddings.
`Embedded connected sum' defines a commutative group structure on 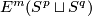 for
for 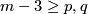 .
See Figure 3.3. of [Skopenkov2006], [Haefliger1966] [Haefliger1966C].
.
See Figure 3.3. of [Skopenkov2006], [Haefliger1966] [Haefliger1966C].
2 General position and the Hopf linking
General Position Theorem 2.1.
For each  -manifold
-manifold  and
and  , every two embeddings
, every two embeddings 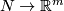 are isotopic.
are isotopic.
The restriction  in Theorem 2.1 is sharp for non-connected manifolds.
in Theorem 2.1 is sharp for non-connected manifolds.
Example: the Hopf linking 2.2.
For each  there is an embedding
there is an embedding 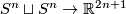 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For  the Hopf Linking is shown in Figure~2.1.a of [Skopenkov2006].
For arbitrary
the Hopf Linking is shown in Figure~2.1.a of [Skopenkov2006].
For arbitrary  (including
(including  ) the image of the Hopf Linking is the union of two
) the image of the Hopf Linking is the union of two  -spheres:
-spheres:
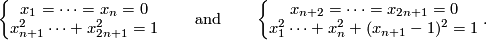
3 The Zeeman construction and linking coefficient
The following table was obtained by Zeeman around 1960:
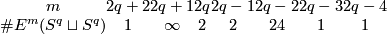
1 Construction of the Zeeman map 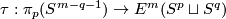
Take 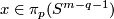 Define embedding
Define embedding 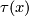 on
on 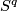 to be the standard embedding into
to be the standard embedding into  .
Take any map
.
Take any map 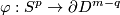 .
Define embedding
.
Define embedding 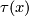 on
on 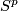 to be the composition
to be the composition
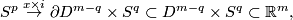
where 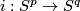 is the equatorial inclusion and the latter inclusion is the standard.
See Figure 3.2 of [Skopenkov2006].
is the equatorial inclusion and the latter inclusion is the standard.
See Figure 3.2 of [Skopenkov2006].
2 Definition of linking coefficient 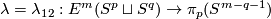 for
for 
Fix orientations of 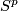 ,
, 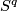 ,
, 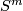 and
and 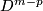 .
Take an embedding
.
Take an embedding  .
Take an embedding
.
Take an embedding 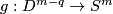 such that
such that 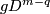 intersects
intersects 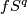 transversally at exactly one point with positive sign (see Figure 3.1 of [Skopenkov2006]).
Then the restriction
transversally at exactly one point with positive sign (see Figure 3.1 of [Skopenkov2006]).
Then the restriction 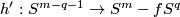 of
of  to
to 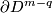 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , the complement
, the complement  is simply-connected.
By Alexander duality
is simply-connected.
By Alexander duality  induces isomorphism in homology.
Hence by Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda(f)=\lambda_{12}(f):=[S^p\overset{f|_{S^p}}\to S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/0/5/c/05c1bffa3c231c4e8f9df10db3009149.png)
Remark 3.1.
(a) Clearly, 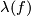 is indeed independent of
is indeed independent of 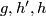 .
.
(b) For 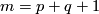 there is a simpler alternative `homological' definition.
That definition works for
there is a simpler alternative `homological' definition.
That definition works for  as well.
as well.
(c) Analogously one can define 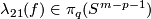 for
for 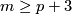 .
.
(d) This definition works for  if
if  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 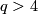 , if the restriction of
, if the restriction of  to
to 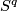 is unknotted).
is unknotted).
(e) Clearly, 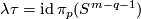 , even for
, even for  .
So
.
So  is surjective and
is surjective and  is injective.
is injective.
3 Classification in the `metastable' range
The Haefliger-Zeeman Theorem 3.2.
If 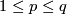 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  and for
and for 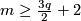 ,
in the PL and DIFF cases, respectively.
,
in the PL and DIFF cases, respectively.
The surjectivity of  (=the injectivity of
(=the injectivity of  ) follows from
) follows from 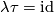 .
The injectivity of
.
The injectivity of  (=the surjectivity of
(=the surjectivity of  ) is proved in [Haefliger1962T], [Zeeman1962]
(or follows from the Haefliger-Weber Theorem 5.4 and Deleted Product Lemma 5.3.a of [Skopenkov2006]).
) is proved in [Haefliger1962T], [Zeeman1962]
(or follows from the Haefliger-Weber Theorem 5.4 and Deleted Product Lemma 5.3.a of [Skopenkov2006]).
4  -invariant
-invariant
By Freudenthal Suspension Theorem 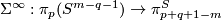 is an isomorphism for
is an isomorphism for
 .
The stable suspension of the linking coefficient can be described alternatively as follows.
For an embedding
.
The stable suspension of the linking coefficient can be described alternatively as follows.
For an embedding  define a map
define a map
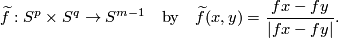
See Figure 3.1 of [Skopenkov2006].
For 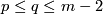 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\to\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/e/f/b/efb0c85d5a9ff128ffcd0895f06d9e69.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 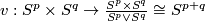 is the quotient map.
See Figure 3.4 of [Skopenkov2006].
The map
is the quotient map.
See Figure 3.4 of [Skopenkov2006].
The map 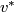 is an isomorphism for
is an isomorphism for 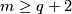 .
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
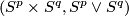 and by the existence of a retraction
and by the existence of a retraction 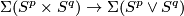 .)
.)
We have 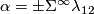 by Lemma 5.1 of [Kervaire1959].
by Lemma 5.1 of [Kervaire1959].
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006].
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006].
4 Invariants
5 Further discussion
6 References
- [Haefliger1962T] Template:Haefliger1962T
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966C] Template:Haefliger1966C
- [Kervaire1959] M. A. Kervaire, A note on obstructions and characteristic classes, Amer. J. Math. 81 (1959), 773–784. MR0107863 (21 #6585) Zbl 0124.16302
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
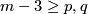 .
See Figure 3.3. of [Skopenkov2006], [Haefliger1966] [Haefliger1966C].
.
See Figure 3.3. of [Skopenkov2006], [Haefliger1966] [Haefliger1966C].
2 General position and the Hopf linking
General Position Theorem 2.1.
For each  -manifold
-manifold  and
and  , every two embeddings
, every two embeddings 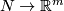 are isotopic.
are isotopic.
The restriction  in Theorem 2.1 is sharp for non-connected manifolds.
in Theorem 2.1 is sharp for non-connected manifolds.
Example: the Hopf linking 2.2.
For each  there is an embedding
there is an embedding 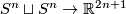 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For  the Hopf Linking is shown in Figure~2.1.a of [Skopenkov2006].
For arbitrary
the Hopf Linking is shown in Figure~2.1.a of [Skopenkov2006].
For arbitrary  (including
(including  ) the image of the Hopf Linking is the union of two
) the image of the Hopf Linking is the union of two  -spheres:
-spheres:
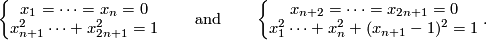
3 The Zeeman construction and linking coefficient
The following table was obtained by Zeeman around 1960:
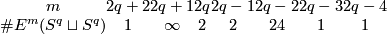
1 Construction of the Zeeman map 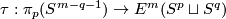
Take 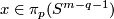 Define embedding
Define embedding 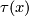 on
on 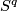 to be the standard embedding into
to be the standard embedding into  .
Take any map
.
Take any map 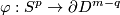 .
Define embedding
.
Define embedding 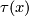 on
on 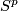 to be the composition
to be the composition
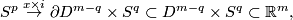
where 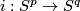 is the equatorial inclusion and the latter inclusion is the standard.
See Figure 3.2 of [Skopenkov2006].
is the equatorial inclusion and the latter inclusion is the standard.
See Figure 3.2 of [Skopenkov2006].
2 Definition of linking coefficient 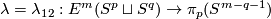 for
for 
Fix orientations of 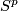 ,
, 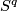 ,
, 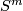 and
and 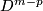 .
Take an embedding
.
Take an embedding  .
Take an embedding
.
Take an embedding 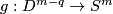 such that
such that 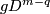 intersects
intersects 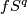 transversally at exactly one point with positive sign (see Figure 3.1 of [Skopenkov2006]).
Then the restriction
transversally at exactly one point with positive sign (see Figure 3.1 of [Skopenkov2006]).
Then the restriction 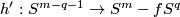 of
of  to
to 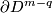 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , the complement
, the complement  is simply-connected.
By Alexander duality
is simply-connected.
By Alexander duality  induces isomorphism in homology.
Hence by Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda(f)=\lambda_{12}(f):=[S^p\overset{f|_{S^p}}\to S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/0/5/c/05c1bffa3c231c4e8f9df10db3009149.png)
Remark 3.1.
(a) Clearly, 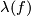 is indeed independent of
is indeed independent of 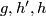 .
.
(b) For 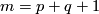 there is a simpler alternative `homological' definition.
That definition works for
there is a simpler alternative `homological' definition.
That definition works for  as well.
as well.
(c) Analogously one can define 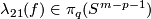 for
for 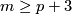 .
.
(d) This definition works for  if
if  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 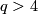 , if the restriction of
, if the restriction of  to
to 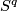 is unknotted).
is unknotted).
(e) Clearly, 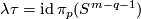 , even for
, even for  .
So
.
So  is surjective and
is surjective and  is injective.
is injective.
3 Classification in the `metastable' range
The Haefliger-Zeeman Theorem 3.2.
If 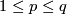 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  and for
and for 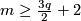 ,
in the PL and DIFF cases, respectively.
,
in the PL and DIFF cases, respectively.
The surjectivity of  (=the injectivity of
(=the injectivity of  ) follows from
) follows from 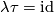 .
The injectivity of
.
The injectivity of  (=the surjectivity of
(=the surjectivity of  ) is proved in [Haefliger1962T], [Zeeman1962]
(or follows from the Haefliger-Weber Theorem 5.4 and Deleted Product Lemma 5.3.a of [Skopenkov2006]).
) is proved in [Haefliger1962T], [Zeeman1962]
(or follows from the Haefliger-Weber Theorem 5.4 and Deleted Product Lemma 5.3.a of [Skopenkov2006]).
4  -invariant
-invariant
By Freudenthal Suspension Theorem 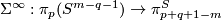 is an isomorphism for
is an isomorphism for
 .
The stable suspension of the linking coefficient can be described alternatively as follows.
For an embedding
.
The stable suspension of the linking coefficient can be described alternatively as follows.
For an embedding  define a map
define a map
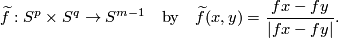
See Figure 3.1 of [Skopenkov2006].
For 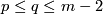 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\to\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/e/f/b/efb0c85d5a9ff128ffcd0895f06d9e69.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 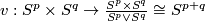 is the quotient map.
See Figure 3.4 of [Skopenkov2006].
The map
is the quotient map.
See Figure 3.4 of [Skopenkov2006].
The map 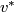 is an isomorphism for
is an isomorphism for 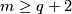 .
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
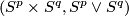 and by the existence of a retraction
and by the existence of a retraction 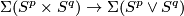 .)
.)
We have 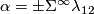 by Lemma 5.1 of [Kervaire1959].
by Lemma 5.1 of [Kervaire1959].
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006].
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006].
4 Invariants
5 Further discussion
6 References
- [Haefliger1962T] Template:Haefliger1962T
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966C] Template:Haefliger1966C
- [Kervaire1959] M. A. Kervaire, A note on obstructions and characteristic classes, Amer. J. Math. 81 (1959), 773–784. MR0107863 (21 #6585) Zbl 0124.16302
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069