High codimension links
Askopenkov (Talk | contribs) (→Classification/Characterization) |
Askopenkov (Talk | contribs) (→The Haefliger-Zeeman classification) |
||
| Line 43: | Line 43: | ||
\end{array}$$ | \end{array}$$ | ||
| − | '' Construction of the Zeeman map $\tau:\pi_p(S^{m-q-1})\to E^m(S^p\sqcup S^q)$ | + | '' Construction of the Zeeman map'' |
| + | $$\tau:\pi_p(S^{m-q-1})\to E^m(S^p\sqcup S^q).$$ | ||
Take $x\in\pi_p(S^{m-q-1})$ | Take $x\in\pi_p(S^{m-q-1})$ | ||
Define embedding $\tau(x)$ on $S^q$ to be the standard embedding into $\R^m$. | Define embedding $\tau(x)$ on $S^q$ to be the standard embedding into $\R^m$. | ||
Revision as of 12:26, 13 February 2013
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
For notation and conventions throughout this page see high codimension embeddings.
2 General position and the Hopf linking
General Position Theorem 2.1.
For each  -manifold
-manifold  and
and  , every two embeddings
, every two embeddings 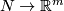 are isotopic.
are isotopic.
The restriction  in Theorem 2.1 is sharp for non-connected manifolds.
in Theorem 2.1 is sharp for non-connected manifolds.
Example: the Hopf linking 2.2.
For each  there is an embedding
there is an embedding 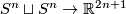 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For  the Hopf Linking is shown in Figure~2.1.a of [Skopenkov2006].
For arbitrary
the Hopf Linking is shown in Figure~2.1.a of [Skopenkov2006].
For arbitrary  (including
(including  ) the image of the Hopf Linking is the union of two
) the image of the Hopf Linking is the union of two  -spheres:
-spheres:
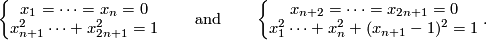
3 The Haefliger-Zeeman classification
The following table was obtained by Zeeman around 1960:
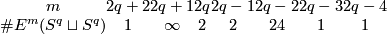
Construction of the Zeeman map
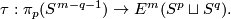
Take 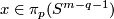 Define embedding
Define embedding 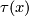 on
on 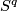 to be the standard embedding into
to be the standard embedding into  .
Take any map
.
Take any map 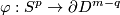 .
Define embedding
.
Define embedding 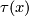 on
on 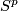 to be the composition
to be the composition
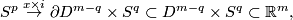
where 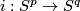 is the equatorial inclusion and the latter inclusion is the standard.
See Figure 3.2 of [Skopenkov2006].
is the equatorial inclusion and the latter inclusion is the standard.
See Figure 3.2 of [Skopenkov2006].
4 Invariants
5 Further discussion
6 References
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.