Group actions on Euclidean spaces
Marek Kaluba (Talk | contribs) (→Definitions) |
Marek Kaluba (Talk | contribs) (→Definitions) |
||
| Line 59: | Line 59: | ||
$$\widetilde{K}Sp(F)\xrightarrow{c_\mathbb{H}}\widetilde{K}U(F)\xrightarrow{r_\mathbb{C}}\widetilde{K}O(F)$$ | $$\widetilde{K}Sp(F)\xrightarrow{c_\mathbb{H}}\widetilde{K}U(F)\xrightarrow{r_\mathbb{C}}\widetilde{K}O(F)$$ | ||
{{beginrem|Definition}} | {{beginrem|Definition}} | ||
| − | For | + | For an abelian group $A$, $\operatorname{qDiv}(A)$ is the subgroup of quasi divisible elements of $A$, i.e., $\operatorname{qDiv}(A)$ is the intersection of the kernels of all homomorphisms from $A$ to free abelian group. |
{{endrem}} | {{endrem}} | ||
</wikitex> | </wikitex> | ||
Revision as of 17:02, 27 November 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Topological actions
...
2 Smooth actions
2.1 Fixed point free
2.1.1 History
The question whether contractible manifolds (e.g. Euclidean spaces) admit smooth fixed point free actions of compact Lie groups has been discussed for the first time by Paul Althaus Smith [Smith1938], [Smith1939], [Smith1941], and [Smith1945]. Conner and Montgomery [Conner&Montgomery1962] have constructed smooth fixed point free actions of  on Euclidean spaces, for
on Euclidean spaces, for 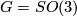 . By generalizing their construction, Hsiang and Hsiang [Hsiang&Hsiang1967] have shown that any non-abelian compact connected Lie group admits such actions.
. By generalizing their construction, Hsiang and Hsiang [Hsiang&Hsiang1967] have shown that any non-abelian compact connected Lie group admits such actions.
For 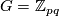 for two relatively primes integers
for two relatively primes integers 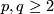 , the construction of Conner and Floyd [Conner&Floyd1959], modified and improved by Kister [Kister1961] and [Kister1963], yields a smooth fixed point free actions on Euclidean spaces (see [Bredon1972, pp. 58-61]). For more general groups
, the construction of Conner and Floyd [Conner&Floyd1959], modified and improved by Kister [Kister1961] and [Kister1963], yields a smooth fixed point free actions on Euclidean spaces (see [Bredon1972, pp. 58-61]). For more general groups  such that there exist a surjection
such that there exist a surjection 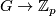 and an injection
and an injection 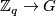 , such actions have been obtained by Edmonds and Lee [Edmonds&Lee1976].
, such actions have been obtained by Edmonds and Lee [Edmonds&Lee1976].
2.1.2 Results
The results of [Conner&Montgomery1962], [Hsiang&Hsiang1967], [Conner&Floyd1959], [Kister1961], and [Edmonds&Lee1976] yield the following theorem.
Theorem 2.1.
A compact Lie group  has smooth fixed point free action on some Euclidean space if and only if at least one of the following conditions holds.
has smooth fixed point free action on some Euclidean space if and only if at least one of the following conditions holds.
- The identity connected component
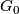 of
of  is non-abelian.
is non-abelian.
- The quotient
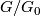 is not of prime power order.
is not of prime power order.
2.2 Fixed point sets
2.2.1 History
2.2.2 Definitions
Let  be a finite group. For two distinct primes
be a finite group. For two distinct primes  and
and  , a
, a  -element of
-element of  is an element of order
is an element of order  . One says that
. One says that  has
has  -dihedral subquotient if
-dihedral subquotient if  contains two subgroups
contains two subgroups  and
and 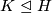 such that
such that 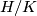 is isomorphic to the dihedral group of order
is isomorphic to the dihedral group of order 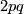 . Denote by
. Denote by 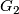 a
a  -Sylow subgroup of
-Sylow subgroup of  .
.
The class of finite groups  not of prime power order divides into the following six mutually disjoint classes.
not of prime power order divides into the following six mutually disjoint classes.
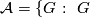 has a
has a  -dihedral subquotient
-dihedral subquotient 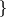 .
.
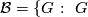 has no
has no  -dihedral subquotient,
-dihedral subquotient,  has a
has a  -element conjugate to its inverse
-element conjugate to its inverse 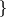 .
.
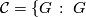 has no
has no  -element conjugate to its inverse,
-element conjugate to its inverse,  has a
has a  -element,
-element, 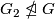
 .
.
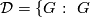 has no
has no  -element conjugate to its inverse,
-element conjugate to its inverse,  has a
has a  -element,
-element, 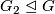
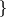 .
.
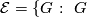 has no
has no  -element,
-element, 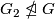
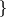 .
.
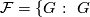 has no
has no  -element,
-element, 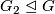
 .
.
Let  be a compact smooth manifold. Between the reduced real, complex, and quaternion
be a compact smooth manifold. Between the reduced real, complex, and quaternion  -theory groups
-theory groups 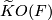 ,
, 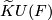 , and
, and 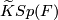 , respectively, consider the induction (complexification and quaternization) homomorphisms
, respectively, consider the induction (complexification and quaternization) homomorphisms 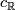 and
and 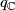 :
:
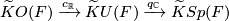
 and
and  :
:
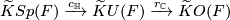
Definition 2.2.
For an abelian group  ,
, 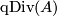 is the subgroup of quasi divisible elements of
is the subgroup of quasi divisible elements of  , i.e.,
, i.e., 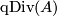 is the intersection of the kernels of all homomorphisms from
is the intersection of the kernels of all homomorphisms from  to free abelian group.
to free abelian group.
2.2.3 Results
Theorem 2.3 ([citation needed]).
Let  be a compact Lie group such that the identity connected component
be a compact Lie group such that the identity connected component 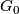 of
of  is non-abelian, or the quotient
is non-abelian, or the quotient 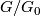 is not of prime power order. Let
is not of prime power order. Let  be a finite dimensional CW-complex. Then the following two statements are equivalent.
be a finite dimensional CW-complex. Then the following two statements are equivalent.
 consists of countable many cells.
consists of countable many cells.
- There exist a finite dimensional, contractible
 -CW-complex
-CW-complex  with finitely many orbit types, such that the fixed point set
with finitely many orbit types, such that the fixed point set 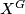 is homeomorphic to
is homeomorphic to  .
.
- There exists a smooth action of
 on some Euclidean space
on some Euclidean space  such that the fixed point set
such that the fixed point set 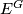 is homotopy equivalent to
is homotopy equivalent to  .
.
It is assumed here, that any smooth manifold admits a countable smooth atlas.
Theorem 2.4 ([Oliver1996]).
Let  be a finite group not of prime power order. Let
be a finite group not of prime power order. Let  be a smooth manifold. Then there exists a smooth action of
be a smooth manifold. Then there exists a smooth action of  on some Euclidean space
on some Euclidean space  such that the fixed point
such that the fixed point 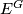 is diffeomorphic to
is diffeomorphic to  if and only if the class
if and only if the class ![[\tau_F]\in \widetilde{K}O(F)](/images/math/f/6/d/f6d05f50857ba929997be0651d9ddfef.png) satisfies the following condition depending on
satisfies the following condition depending on  .
.
- If
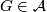 , then there is no restriction on
, then there is no restriction on ![[\tau_F]](/images/math/4/3/c/43c708b9317aab9c266b5c48be3b4214.png) .
.
- If
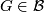 , then
, then ![c_{\mathbb{R}}([\tau_F])\in c_{\mathbb{H}}(\widetilde{K}Sp(F))+\text{qDiv}(\widetilde{K}U(F))](/images/math/1/e/c/1ec8e1af1ec551a8e4119099f322eae1.png) .
.
- If
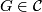 , then
, then ![[\tau_F]\in r_{\mathbb{C}}(\widetilde{K}U(F))+\text{qDiv}(\widetilde{K}O(F))](/images/math/0/4/5/0459d71bef36b11b947b76165cc7dd50.png) .
.
- If
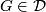 , then
, then ![[\tau_F]\in r_{\mathbb{C}}(\widetilde{K}U(F))](/images/math/c/c/3/cc3bee2faf57205cef8db8bfa608aa81.png) , i.e.,
, i.e.,  is stably complex.
is stably complex.
- If
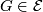 , then
, then ![[\tau_F]\in\text{qDiv}(\widetilde{K}O(F))](/images/math/1/2/7/1275ffcdcd540c823d27027ea44e8cac.png) .
.
- If
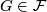 , then
, then ![[\tau_F]\in r_{\mathbb{C}}(\text{qDiv}(\widetilde{K}U(F)))](/images/math/c/8/a/c8a3d9216412a6f3b372f0e6a2615ac1.png) .
.
3 References
- [Bredon1972] G. E. Bredon, Introduction to compact transformation groups, Academic Press, New York, 1972. MR0413144 (54 #1265) Zbl 0484.57001
- [Conner&Floyd1959] P. E. Conner and E. E. Floyd, On the construction of periodic maps without fixed points, Proc. Amer. Math. Soc. 10 (1959), 354–360. MR0105115 (21 #3860) Zbl 0092.39701
- [Conner&Montgomery1962] P. Conner and D. Montgomery, An example for
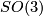 , Proc. Nat. Acad. Sci. U.S.A. 48 (1962), 1918–1922. MR0148795 (26 #6300) Zbl 0107.16604
, Proc. Nat. Acad. Sci. U.S.A. 48 (1962), 1918–1922. MR0148795 (26 #6300) Zbl 0107.16604
- [Edmonds&Lee1976] A. L. Edmonds and R. Lee, Compact Lie groups which act on Euclidean space without fixed points, Proc. Amer. Math. Soc. 55 (1976), no.2, 416–418. MR0420672 (54 #8684) Zbl 0326.57011
- [Hsiang&Hsiang1967] W. Hsiang and W. Hsiang, Differentiable actions of compact connected classical groups. I, Amer. J. Math. 89 (1967), 705–786. MR0217213 (36 #304) Zbl 0205.53902
- [Kister1961] J. M. Kister, Examples of periodic maps on Euclidean spaces without fixed points. , Bull. Amer. Math. Soc. 67 (1961), 471–474. MR0130929 (24 #A783) Zbl 0101.15602
- [Kister1963] J. M. Kister, Differentiable periodic actions on
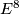 without fixed points, Amer. J. Math. 85 (1963), 316–319. MR0154278 (27 #4227) Zbl 0119.18801
without fixed points, Amer. J. Math. 85 (1963), 316–319. MR0154278 (27 #4227) Zbl 0119.18801
- [Oliver1996] B. Oliver, Fixed point sets and tangent bundles of actions on disks and Euclidean spaces, Topology 35 (1996), no.3, 583–615. MR1396768 (97g:57059) Zbl 0861.57047
- [Smith1938] P. A. Smith, Transformations of finite period, Ann. of Math. (2) 39 (1938), no.1, 127–164. MR1503393 Zbl 0063.07093
- [Smith1939] P. A. Smith, Transformations of finite period. II, Ann. of Math. (2) 40 (1939), 690–711. MR0000177 (1,30c) Zbl 0063.07093
- [Smith1941] P. A. Smith, Transformations of finite period. III. Newman's theorem, Ann. of Math. (2) 42 (1941), 446–458. MR0004128 (2,324c)
- [Smith1945] P. A. Smith, Transformations of finite period. IV. Dimensional parity, Ann. of Math. (2) 46 (1945), 357–364. MR0013304 (7,136e) Zbl 0063.07093
- [citation needed] Template:Citation needed