Group actions on Euclidean spaces
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Topological actions
...
[edit] 2 Smooth actions
[edit] 2.1 Fixed point free
[edit] 2.1.1 History
The question whether contractible manifolds such as Euclidean spaces admit smooth fixed point free actions of compact Lie groups has been discussed for the first time by Paul Althaus Smith [Smith1938], [Smith1939], [Smith1941], and [Smith1945]. For 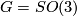 , Conner and Montgomery [Conner&Montgomery1962] have constructed smooth fixed point free actions of
, Conner and Montgomery [Conner&Montgomery1962] have constructed smooth fixed point free actions of  on Euclidean spaces. By generalizing their construction, Hsiang and Hsiang [Hsiang&Hsiang1967] have shown that any non-abelian compact connected Lie group
on Euclidean spaces. By generalizing their construction, Hsiang and Hsiang [Hsiang&Hsiang1967] have shown that any non-abelian compact connected Lie group  can admit such actions.
can admit such actions.
Let 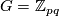 for two relatively primes integers
for two relatively primes integers 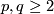 . The construction of Conner and Floyd [Conner&Floyd1959], modified and improved by Kister [Kister1961] and [Kister1963], yields smooth fixed point free actions of
. The construction of Conner and Floyd [Conner&Floyd1959], modified and improved by Kister [Kister1961] and [Kister1963], yields smooth fixed point free actions of  on Euclidean spaces (see [Bredon1972, pp. 58-61]). In the more general case of
on Euclidean spaces (see [Bredon1972, pp. 58-61]). In the more general case of  where there exist a surjection
where there exist a surjection 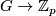 and an injection
and an injection 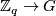 , smooth fixed point free actions of
, smooth fixed point free actions of  on Euclidean spaces have been constructed by Edmonds and Lee [Edmonds&Lee1976].
on Euclidean spaces have been constructed by Edmonds and Lee [Edmonds&Lee1976].
[edit] 2.1.2 Results
The results of [Conner&Montgomery1962], [Hsiang&Hsiang1967], [Conner&Floyd1959], [Kister1961], and [Edmonds&Lee1976] yield the following two theorems.
Theorem 2.1.
A compact Lie group  admits a smooth fixed point free action on some Euclidean space if and only if the identity connected component
admits a smooth fixed point free action on some Euclidean space if and only if the identity connected component 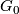 of
of  is non-abelian or the quotient group
is non-abelian or the quotient group 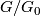 is not of prime power order.
is not of prime power order.
Theorem 2.2.
Let  be a compact Lie group such that the identity connected component
be a compact Lie group such that the identity connected component 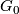 of
of  is non-abelian or the quotient group
is non-abelian or the quotient group 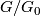 is not of prime power order. Let
is not of prime power order. Let  be a CW complex. Then the following three statements are equivalent.
be a CW complex. Then the following three statements are equivalent.
 is finite dimensional and countable (i.e., consists of countably many cells).
is finite dimensional and countable (i.e., consists of countably many cells).
- There exist a finite dimensional, countable, contractible
 -CW-complex
-CW-complex  with finitely many orbit types, such that the fixed point set
with finitely many orbit types, such that the fixed point set 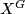 is homeomorphic to
is homeomorphic to  .
.
- There exists a smooth action of
 on some Euclidean space
on some Euclidean space  such that the fixed point set
such that the fixed point set 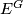 is homotopy equivalent to
is homotopy equivalent to  .
.
[edit] 2.2 Fixed point sets
[edit] 2.2.1 History
[edit] 2.2.2 Definitions
For a space  , between the reduced real, complex, and quaternion
, between the reduced real, complex, and quaternion  -theory groups
-theory groups 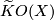 ,
, 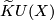 , and
, and 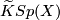 , respectively, consider
, respectively, consider
- the induction (complexification and quaternization) homomorphisms
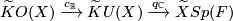
- and the forgetful (complexification and realification) homomorphisms
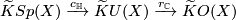 .
.
Definition 2.3.
An element of an abelian group  is called quasi-divisible if it belongs to the intersection of the kernels of all homomorphisms from
is called quasi-divisible if it belongs to the intersection of the kernels of all homomorphisms from  to free abelian groups.
to free abelian groups.
The subgroup of quasi-divisible elements of  is denoted by
is denoted by 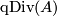 .
.
Remark 2.4.
If an abelian group  is finitely generated, then
is finitely generated, then 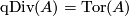 , the group of torsion elements of
, the group of torsion elements of  .
.
[edit] 2.2.3 Results
Theorem 2.5 ([Oliver1996]).
Let  be a finite group not of prime power order, and let
be a finite group not of prime power order, and let 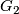 denote a
denote a  -Sylow subgroup of
-Sylow subgroup of  . Let
. Let  be a smooth manifold. Then there exists a smooth action of
be a smooth manifold. Then there exists a smooth action of  on some Euclidean space
on some Euclidean space  such that the fixed point
such that the fixed point 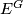 is diffeomorphic to
is diffeomorphic to  if and only if the following two statements hold.
if and only if the following two statements hold.
-
 has a countable base of topology and
has a countable base of topology and 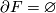 .
.
- The class
![[\tau_F]](/images/math/4/3/c/43c708b9317aab9c266b5c48be3b4214.png) of
of 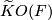 satisfies the following condition depending on
satisfies the following condition depending on  .
.
-
![[\tau_F]](/images/math/4/3/c/43c708b9317aab9c266b5c48be3b4214.png) is arbitrary, if
is arbitrary, if  is in the class
is in the class 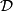 of finite groups with dihedral subquotient of order
of finite groups with dihedral subquotient of order 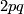 for two distinct primes
for two distinct primes  and
and  .
.
-
![c_{\mathbb{R}}([\tau_F])\in c_{\mathbb{H}}(\widetilde{K}Sp(F))+\text{qDiv}(\widetilde{K}U(F))](/images/math/1/e/c/1ec8e1af1ec551a8e4119099f322eae1.png) , if
, if  has a composite order element conjugate to its inverse and
has a composite order element conjugate to its inverse and 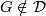 .
.
-
![[\tau_F]\in r_{\mathbb{C}}(\widetilde{K}U(F))+\text{qDiv}(\widetilde{K}O(F))](/images/math/0/4/5/0459d71bef36b11b947b76165cc7dd50.png) , if
, if  has a composite order element but never conjugate to its inverse and
has a composite order element but never conjugate to its inverse and 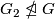 .
.
-
![[\tau_F]\in r_{\mathbb{C}}(\widetilde{K}U(F))](/images/math/c/c/3/cc3bee2faf57205cef8db8bfa608aa81.png) , i.e.,
, i.e.,  is stably complex, if
is stably complex, if  has a composite order element but never conjugate to its inverse and
has a composite order element but never conjugate to its inverse and 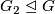 .
.
-
![[\tau_F]\in\text{qDiv}(\widetilde{K}O(F))](/images/math/1/2/7/1275ffcdcd540c823d27027ea44e8cac.png) , if
, if  has no composite order element and
has no composite order element and 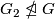 .
.
-
![[\tau_F]\in r_{\mathbb{C}}(\text{qDiv}(\widetilde{K}U(F)))](/images/math/c/8/a/c8a3d9216412a6f3b372f0e6a2615ac1.png) , if
, if  has no composite order element and
has no composite order element and 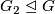 .
.
-
[edit] 3 References
- [Bredon1972] G. E. Bredon, Introduction to compact transformation groups, Academic Press, New York, 1972. MR0413144 (54 #1265) Zbl 0484.57001
- [Conner&Floyd1959] P. E. Conner and E. E. Floyd, On the construction of periodic maps without fixed points, Proc. Amer. Math. Soc. 10 (1959), 354–360. MR0105115 (21 #3860) Zbl 0092.39701
- [Conner&Montgomery1962] P. Conner and D. Montgomery, An example for
 , Proc. Nat. Acad. Sci. U.S.A. 48 (1962), 1918–1922. MR0148795 (26 #6300) Zbl 0107.16604
, Proc. Nat. Acad. Sci. U.S.A. 48 (1962), 1918–1922. MR0148795 (26 #6300) Zbl 0107.16604
- [Edmonds&Lee1976] A. L. Edmonds and R. Lee, Compact Lie groups which act on Euclidean space without fixed points, Proc. Amer. Math. Soc. 55 (1976), no.2, 416–418. MR0420672 (54 #8684) Zbl 0326.57011
- [Hsiang&Hsiang1967] W. Hsiang and W. Hsiang, Differentiable actions of compact connected classical groups. I, Amer. J. Math. 89 (1967), 705–786. MR0217213 (36 #304) Zbl 0205.53902
- [Kister1961] J. M. Kister, Examples of periodic maps on Euclidean spaces without fixed points. , Bull. Amer. Math. Soc. 67 (1961), 471–474. MR0130929 (24 #A783) Zbl 0101.15602
- [Kister1963] J. M. Kister, Differentiable periodic actions on
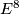 without fixed points, Amer. J. Math. 85 (1963), 316–319. MR0154278 (27 #4227) Zbl 0119.18801
without fixed points, Amer. J. Math. 85 (1963), 316–319. MR0154278 (27 #4227) Zbl 0119.18801
- [Oliver1996] B. Oliver, Fixed point sets and tangent bundles of actions on disks and Euclidean spaces, Topology 35 (1996), no.3, 583–615. MR1396768 (97g:57059) Zbl 0861.57047
- [Smith1938] P. A. Smith, Transformations of finite period, Ann. of Math. (2) 39 (1938), no.1, 127–164. MR1503393 Zbl 0063.07093
- [Smith1939] P. A. Smith, Transformations of finite period. II, Ann. of Math. (2) 40 (1939), 690–711. MR0000177 (1,30c) Zbl 0063.07093
- [Smith1941] P. A. Smith, Transformations of finite period. III. Newman's theorem, Ann. of Math. (2) 42 (1941), 446–458. MR0004128 (2,324c)
- [Smith1945] P. A. Smith, Transformations of finite period. IV. Dimensional parity, Ann. of Math. (2) 46 (1945), 357–364. MR0013304 (7,136e) Zbl 0063.07093