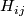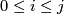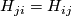Formal group laws and genera
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:29, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Taras Panov. No other user may edit this page at present. |
Contents |
1 Introduction
The theory of formal group laws, originally appeared in algebraic geometry, has been brought into the bordism theory in the pioneering work [Novikov1967]. The applications of formal group laws in algebraic topology are closely connected with the Hirzebruch genera [Hirzebruch1966], one of the most important class of invariants of bordism classes of manifolds.
2 Elements of the theory of formal group laws
Let  be a commutative ring with unit.
be a commutative ring with unit.
A formal power series ![F(u,v)\in R[[u,v]]](/images/math/7/4/f/74f4f62ad66dd8d43f3631de0acc5087.png) is called a
(commutative one-dimensional) formal group law over
is called a
(commutative one-dimensional) formal group law over  if
it satisfies the following equations:
if
it satisfies the following equations:
-
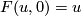 ,
, 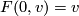 ;
;
-
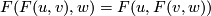 ;
;
-
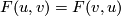 .
.
The original example of a formal group law over a field 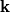 is
provided by the expansion near the unit of the multiplication map
is
provided by the expansion near the unit of the multiplication map
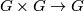 in a one-dimensional algebraic group over
in a one-dimensional algebraic group over 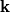 .
This also explains the terminology.
.
This also explains the terminology.
A formal group law  over
over  is called linearisable if
there exists a coordinate change
is called linearisable if
there exists a coordinate change ![u\mapsto g_F(u)=u+\sum_{i>0}g_iu^i\in R[[u]]](/images/math/4/0/2/402275b06df1121bd77c1e46f1b386dd.png) such that
such that
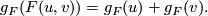
Note that every formal group law over  determines a formal
group law over
determines a formal
group law over  .
.
Theorem 2.1.
Every formal group law  is linearisable over
is linearisable over  .
.
Proof. Consider the series 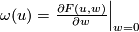 . Then
. Then
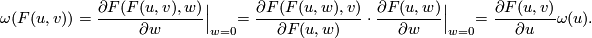
We therefore have
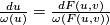 . Set
. Set
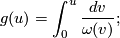
then 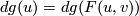 . This implies that
. This implies that 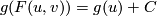 .
Since
.
Since 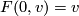 and
and 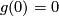 , we get
, we get 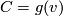 . Thus,
. Thus,
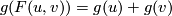 .
. 
A series 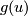 satisfying the equation
satisfying the equation 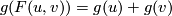 is called
the logarithm of the formal group law
is called
the logarithm of the formal group law  ; the above Theorem
shows that a formal group law over
; the above Theorem
shows that a formal group law over  always has a logarithm. Its functional inverse series
always has a logarithm. Its functional inverse series
![f(t)\in R\otimes\mathbb Q[[t]]](/images/math/d/8/d/d8df1357c59114c6756e554a41d3d2cb.png) is called the exponential of
the formal group law, so that we have
is called the exponential of
the formal group law, so that we have 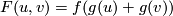 over
over  . If
. If  does not have torsion (i.e.
does not have torsion (i.e. 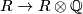 is monic), the latter formula shows that a formal group law (as a series with coefficients in
is monic), the latter formula shows that a formal group law (as a series with coefficients in  ) is fully
determined by its logarithm (which is a series with coefficients in
) is fully
determined by its logarithm (which is a series with coefficients in  ).
).
Let 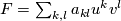 be a formal group law over a ring
be a formal group law over a ring
 and
and 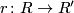 a ring homomorphism. Denote by
a ring homomorphism. Denote by 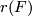 the formal series
the formal series ![\sum_{k,l}r(a_{kl})u^kv^l\in R'[[u,v]]](/images/math/7/9/f/79f6c5bbdc00bf4b92d352b3ad689c32.png) ; then
; then
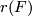 is a formal group law over
is a formal group law over 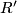 .
.
A formal group law  over a ring
over a ring  is universal if
for any formal group law
is universal if
for any formal group law  over any ring
over any ring  there exists a
unique homomorphism
there exists a
unique homomorphism 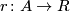 such that
such that 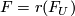 .
.
Proposition 2.2.
Assume that the universal formal group law  over
over  exists.
Then
exists.
Then
- The ring
 is multiplicatively generated by the coefficients of the series
is multiplicatively generated by the coefficients of the series  ;
;
- The universal formal group law is unique: if
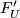 is another universal formal group law over
is another universal formal group law over 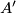 , then there is an isomorphism
, then there is an isomorphism 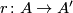 such that
such that 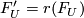 .
.
Proof. To prove the first statement, denote by 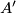 the subring in
the subring in  generated by the coefficients of
generated by the coefficients of  . Then there is a
monomorphism
. Then there is a
monomorphism 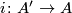 satisfying
satisfying 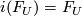 . On the
other hand, by universality there exists a homomorphism
. On the
other hand, by universality there exists a homomorphism 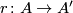 satisfying
satisfying 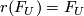 . It follows that
. It follows that 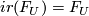 .
This implies that
.
This implies that 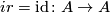 by the uniqueness
requirement in the definition of
by the uniqueness
requirement in the definition of  . Thus
. Thus 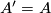 . The second
statement is proved similarly.
. The second
statement is proved similarly. 
Theorem 2.3 ([Lazard1955]).
The universal formal group law  exists, and its coefficient
ring
exists, and its coefficient
ring  is isomorphic to the polynomial ring
is isomorphic to the polynomial ring ![\mathbb Z[a_1,a_2,\ldots]](/images/math/8/2/c/82c9310fe354b92a2a7693849d745f6e.png) on an infinite number of generators.
on an infinite number of generators.
3 Formal group law of geometric cobordisms
The applications of the formal group laws in the cobordism theory build upon the following basic example.
Let  be a cell complex and
be a cell complex and 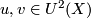 two geometric cobordisms
corresponding to elements
two geometric cobordisms
corresponding to elements 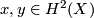 respectively. Denote by
respectively. Denote by
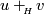 the geometric cobordism corresponding to the
cohomology class
the geometric cobordism corresponding to the
cohomology class 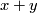 .
.
Proposition 3.1.
The following relation holds in 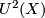 :
:
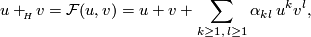
where the coefficients 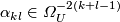 do
not depend on
do
not depend on  . The series
. The series 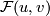 is a formal group law over the complex bordism
ring
is a formal group law over the complex bordism
ring 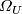 .
.
See the proof.
The series 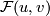 is called the formal group law of
geometric cobordisms; nowadays it is also usually referred to as "complex cobordism formal group law".
is called the formal group law of
geometric cobordisms; nowadays it is also usually referred to as "complex cobordism formal group law".
The geometric cobordism 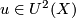 is the
first Chern-Conner-Floyd class of the complex line bundle
is the
first Chern-Conner-Floyd class of the complex line bundle
 over
over  obtained by pulling back the canonical bundle along
the map
obtained by pulling back the canonical bundle along
the map 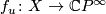 . It follows that the formal
group law of geometric cobordisms gives an expression of the first
class
. It follows that the formal
group law of geometric cobordisms gives an expression of the first
class 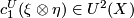 of the tensor product of
two complex line bundles over
of the tensor product of
two complex line bundles over  in terms of the classes
in terms of the classes
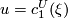 and
and 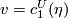 of the factors:
of the factors:
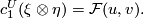
The next statement describes manifolds representing the coefficients of the formal group law of geometric cobordisms.
See the proof.
Theorem 3.3 (Mishchenko, see [Novikov1967]). The logarithm of the formal group law of geometric cobordisms is given by the series
![\displaystyle g_{\mathcal F}(u)=u+\sum_{k\ge1}\frac{[\mathbb C P^k]}{k+1}u^{k+1} \in\varOmega_U\otimes\mathbb Q[[u]].](/images/math/d/1/d/d1db6dc3034e8a8e12ce289fee9dd6ee.png)
See the proof.
Theorem 3.4 ([Quillen1969]).
The formal group law 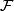 of geometric cobordisms
of geometric cobordisms
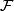 is universal.
is universal.
See the proof.
The earliest applications of the formal group laws in cobordism concerned finite group actions on manifolds, or "Differentiable periodic maps", see [Novikov1967], [Buchstaber&Novikov1971], [Buchstaber&Mishchenko&Novikov1971]. For instance, a theorem of [Novikov1967] describes the complex cobordism ring of the classifying space of the group 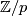 as
as
![\displaystyle U^*(B\mathbb Z/p)\cong\varOmega_U[[u]]/[u]_p,](/images/math/b/d/7/bd7da689ff14861c5d795b6b619a1156.png)
where ![\varOmega_U[[u]]](/images/math/3/f/e/3feba2059a53a5fbe5610295beed27ae.png) denotes the ring of power series in one generator
denotes the ring of power series in one generator  of degree 2 with coefficients in
of degree 2 with coefficients in 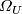 , and
, and ![[u]_p](/images/math/a/c/5/ac5fed2f54cfbb3ddc12cfb9fd265a2b.png) denotes the
denotes the  th power in the formal group law of geometric cobordisms. This result extended and unified many earlier calculations of bordisms with
th power in the formal group law of geometric cobordisms. This result extended and unified many earlier calculations of bordisms with 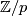 -actions from [Conner&Floyd1964].
-actions from [Conner&Floyd1964].
The universality of the formal group law of geometric cobordism has important consequences for the stable homotopy theory: it implies that complex bordism is the universal complex oriented cohomology theory.
4 Hirzebruch genera
5 References
- [Buchstaber&Mishchenko&Novikov1971] V. M. Buhštaber, A. S. Mišcenko and S. P. Novikov, Formal groups and their role in the apparatus of algebraic topology, Uspehi Mat. Nauk 26 (1971), no.2(158), 131–154. MR0445522 (56 #3862) Zbl 0226.55007
- [Buchstaber&Novikov1971] V. M. Buhštaber and S. P. Novikov, Formal groups, power systems and Adams operators, Mat. Sb. (N.S.) 84(126) (1971), 81–118. MR0291159 (45 #253) Zbl 0239.55005
- [Buchstaber1970] V. M. Buhštaber, The Chern-Dold character in cobordisms. I, Mat. Sb. (N.S.) 83 (125) (1970), 575–595. MR0273630 (42 #8507) Zbl 0219.57027
- [Conner&Floyd1964] P. E. Conner and E. E. Floyd, Differentiable periodic maps, Academic Press Inc., Publishers, New York, 1964. MR0176478 (31 #750) Zbl 0417.57019
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Lazard1955] M. Lazard, Sur les groupes de Lie formels à un paramètre, Bull. Soc. Math. France 83 (1955), 251–274. MR0073925 (17,508e) Zbl 0068.25703
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
- [Quillen1969] D. Quillen, On the formal group laws of unoriented and complex cobordism theory, Bull. Amer. Math. Soc. 75 (1969), 1293–1298. MR0253350 (40 #6565) Zbl 0199.26705
|
This page has not been refereed. The information given here might be incomplete or provisional. |
A formal power series ![F(u,v)\in R[[u,v]]](/images/math/7/4/f/74f4f62ad66dd8d43f3631de0acc5087.png) is called a
(commutative one-dimensional) formal group law over
is called a
(commutative one-dimensional) formal group law over  if
it satisfies the following equations:
if
it satisfies the following equations:
-
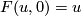 ,
, 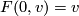 ;
;
-
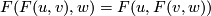 ;
;
-
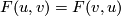 .
.
The original example of a formal group law over a field 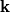 is
provided by the expansion near the unit of the multiplication map
is
provided by the expansion near the unit of the multiplication map
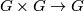 in a one-dimensional algebraic group over
in a one-dimensional algebraic group over 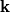 .
This also explains the terminology.
.
This also explains the terminology.
A formal group law  over
over  is called linearisable if
there exists a coordinate change
is called linearisable if
there exists a coordinate change ![u\mapsto g_F(u)=u+\sum_{i>0}g_iu^i\in R[[u]]](/images/math/4/0/2/402275b06df1121bd77c1e46f1b386dd.png) such that
such that
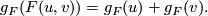
Note that every formal group law over  determines a formal
group law over
determines a formal
group law over  .
.
Theorem 2.1.
Every formal group law  is linearisable over
is linearisable over  .
.
Proof. Consider the series 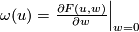 . Then
. Then
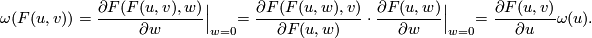
We therefore have
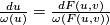 . Set
. Set
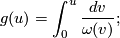
then 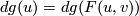 . This implies that
. This implies that 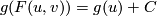 .
Since
.
Since 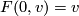 and
and 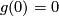 , we get
, we get 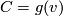 . Thus,
. Thus,
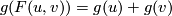 .
. 
A series 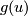 satisfying the equation
satisfying the equation 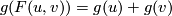 is called
the logarithm of the formal group law
is called
the logarithm of the formal group law  ; the above Theorem
shows that a formal group law over
; the above Theorem
shows that a formal group law over  always has a logarithm. Its functional inverse series
always has a logarithm. Its functional inverse series
![f(t)\in R\otimes\mathbb Q[[t]]](/images/math/d/8/d/d8df1357c59114c6756e554a41d3d2cb.png) is called the exponential of
the formal group law, so that we have
is called the exponential of
the formal group law, so that we have 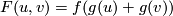 over
over  . If
. If  does not have torsion (i.e.
does not have torsion (i.e. 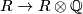 is monic), the latter formula shows that a formal group law (as a series with coefficients in
is monic), the latter formula shows that a formal group law (as a series with coefficients in  ) is fully
determined by its logarithm (which is a series with coefficients in
) is fully
determined by its logarithm (which is a series with coefficients in  ).
).
Let 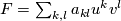 be a formal group law over a ring
be a formal group law over a ring
 and
and 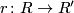 a ring homomorphism. Denote by
a ring homomorphism. Denote by 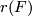 the formal series
the formal series ![\sum_{k,l}r(a_{kl})u^kv^l\in R'[[u,v]]](/images/math/7/9/f/79f6c5bbdc00bf4b92d352b3ad689c32.png) ; then
; then
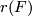 is a formal group law over
is a formal group law over 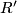 .
.
A formal group law  over a ring
over a ring  is universal if
for any formal group law
is universal if
for any formal group law  over any ring
over any ring  there exists a
unique homomorphism
there exists a
unique homomorphism 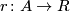 such that
such that 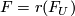 .
.
Proposition 2.2.
Assume that the universal formal group law  over
over  exists.
Then
exists.
Then
- The ring
 is multiplicatively generated by the coefficients of the series
is multiplicatively generated by the coefficients of the series  ;
;
- The universal formal group law is unique: if
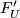 is another universal formal group law over
is another universal formal group law over 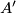 , then there is an isomorphism
, then there is an isomorphism 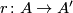 such that
such that 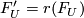 .
.
Proof. To prove the first statement, denote by 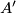 the subring in
the subring in  generated by the coefficients of
generated by the coefficients of  . Then there is a
monomorphism
. Then there is a
monomorphism 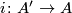 satisfying
satisfying 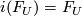 . On the
other hand, by universality there exists a homomorphism
. On the
other hand, by universality there exists a homomorphism 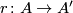 satisfying
satisfying 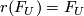 . It follows that
. It follows that 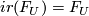 .
This implies that
.
This implies that 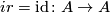 by the uniqueness
requirement in the definition of
by the uniqueness
requirement in the definition of  . Thus
. Thus 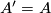 . The second
statement is proved similarly.
. The second
statement is proved similarly. 
Theorem 2.3 ([Lazard1955]).
The universal formal group law  exists, and its coefficient
ring
exists, and its coefficient
ring  is isomorphic to the polynomial ring
is isomorphic to the polynomial ring ![\mathbb Z[a_1,a_2,\ldots]](/images/math/8/2/c/82c9310fe354b92a2a7693849d745f6e.png) on an infinite number of generators.
on an infinite number of generators.
3 Formal group law of geometric cobordisms
The applications of the formal group laws in the cobordism theory build upon the following basic example.
Let  be a cell complex and
be a cell complex and 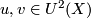 two geometric cobordisms
corresponding to elements
two geometric cobordisms
corresponding to elements 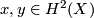 respectively. Denote by
respectively. Denote by
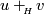 the geometric cobordism corresponding to the
cohomology class
the geometric cobordism corresponding to the
cohomology class 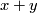 .
.
Proposition 3.1.
The following relation holds in 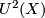 :
:
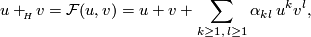
where the coefficients 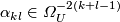 do
not depend on
do
not depend on  . The series
. The series 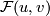 is a formal group law over the complex bordism
ring
is a formal group law over the complex bordism
ring 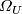 .
.
See the proof.
The series 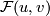 is called the formal group law of
geometric cobordisms; nowadays it is also usually referred to as "complex cobordism formal group law".
is called the formal group law of
geometric cobordisms; nowadays it is also usually referred to as "complex cobordism formal group law".
The geometric cobordism 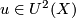 is the
first Chern-Conner-Floyd class of the complex line bundle
is the
first Chern-Conner-Floyd class of the complex line bundle
 over
over  obtained by pulling back the canonical bundle along
the map
obtained by pulling back the canonical bundle along
the map 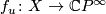 . It follows that the formal
group law of geometric cobordisms gives an expression of the first
class
. It follows that the formal
group law of geometric cobordisms gives an expression of the first
class 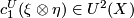 of the tensor product of
two complex line bundles over
of the tensor product of
two complex line bundles over  in terms of the classes
in terms of the classes
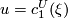 and
and 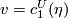 of the factors:
of the factors:
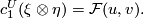
The next statement describes manifolds representing the coefficients of the formal group law of geometric cobordisms.
See the proof.
Theorem 3.3 (Mishchenko, see [Novikov1967]). The logarithm of the formal group law of geometric cobordisms is given by the series
![\displaystyle g_{\mathcal F}(u)=u+\sum_{k\ge1}\frac{[\mathbb C P^k]}{k+1}u^{k+1} \in\varOmega_U\otimes\mathbb Q[[u]].](/images/math/d/1/d/d1db6dc3034e8a8e12ce289fee9dd6ee.png)
See the proof.
Theorem 3.4 ([Quillen1969]).
The formal group law 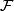 of geometric cobordisms
of geometric cobordisms
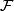 is universal.
is universal.
See the proof.
The earliest applications of the formal group laws in cobordism concerned finite group actions on manifolds, or "Differentiable periodic maps", see [Novikov1967], [Buchstaber&Novikov1971], [Buchstaber&Mishchenko&Novikov1971]. For instance, a theorem of [Novikov1967] describes the complex cobordism ring of the classifying space of the group 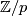 as
as
![\displaystyle U^*(B\mathbb Z/p)\cong\varOmega_U[[u]]/[u]_p,](/images/math/b/d/7/bd7da689ff14861c5d795b6b619a1156.png)
where ![\varOmega_U[[u]]](/images/math/3/f/e/3feba2059a53a5fbe5610295beed27ae.png) denotes the ring of power series in one generator
denotes the ring of power series in one generator  of degree 2 with coefficients in
of degree 2 with coefficients in 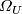 , and
, and ![[u]_p](/images/math/a/c/5/ac5fed2f54cfbb3ddc12cfb9fd265a2b.png) denotes the
denotes the  th power in the formal group law of geometric cobordisms. This result extended and unified many earlier calculations of bordisms with
th power in the formal group law of geometric cobordisms. This result extended and unified many earlier calculations of bordisms with 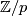 -actions from [Conner&Floyd1964].
-actions from [Conner&Floyd1964].
The universality of the formal group law of geometric cobordism has important consequences for the stable homotopy theory: it implies that complex bordism is the universal complex oriented cohomology theory.
4 Hirzebruch genera
5 References
- [Buchstaber&Mishchenko&Novikov1971] V. M. Buhštaber, A. S. Mišcenko and S. P. Novikov, Formal groups and their role in the apparatus of algebraic topology, Uspehi Mat. Nauk 26 (1971), no.2(158), 131–154. MR0445522 (56 #3862) Zbl 0226.55007
- [Buchstaber&Novikov1971] V. M. Buhštaber and S. P. Novikov, Formal groups, power systems and Adams operators, Mat. Sb. (N.S.) 84(126) (1971), 81–118. MR0291159 (45 #253) Zbl 0239.55005
- [Buchstaber1970] V. M. Buhštaber, The Chern-Dold character in cobordisms. I, Mat. Sb. (N.S.) 83 (125) (1970), 575–595. MR0273630 (42 #8507) Zbl 0219.57027
- [Conner&Floyd1964] P. E. Conner and E. E. Floyd, Differentiable periodic maps, Academic Press Inc., Publishers, New York, 1964. MR0176478 (31 #750) Zbl 0417.57019
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Lazard1955] M. Lazard, Sur les groupes de Lie formels à un paramètre, Bull. Soc. Math. France 83 (1955), 251–274. MR0073925 (17,508e) Zbl 0068.25703
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
- [Quillen1969] D. Quillen, On the formal group laws of unoriented and complex cobordism theory, Bull. Amer. Math. Soc. 75 (1969), 1293–1298. MR0253350 (40 #6565) Zbl 0199.26705
|
This page has not been refereed. The information given here might be incomplete or provisional. |
![\displaystyle \mathcal F(u,v)=\frac{\sum_{i,j\ge0}[H_{ij}]u^iv^j} {\bigl(\sum_{r\ge0}[\mathbb C P^r]u^r\bigr)\bigl(\sum_{s\ge0}[\mathbb C P^s]v^s\bigr)},](/images/math/0/4/7/047277326106a8d596df93ae07b21b2e.png)