Formal group laws and genera
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:29, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Taras Panov. No other user may edit this page at present. |
Contents |
1 Introduction
The theory of formal group laws, originally appeared in algebraic geometry, has been brought into the bordism theory in the pioneering work [Novikov1967]. The applications of formal group laws in algebraic topology are closely connected with the Hirzebruch genera [Hirzebruch1966], one of the most important class of invariants of bordism classes of manifolds.
2 Elements of the theory of formal group laws
Let  be a commutative ring with unit.
be a commutative ring with unit.
A formal power series ![F(u,v)\in R[[u,v]]](/images/math/7/4/f/74f4f62ad66dd8d43f3631de0acc5087.png) is called a
(commutative one-dimensional) formal group law over
is called a
(commutative one-dimensional) formal group law over  if
it satisfies the following equations:
if
it satisfies the following equations:
-
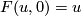 ,
, 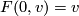 ;
;
-
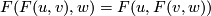 ;
;
-
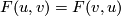 .
.
The original example of a formal group law over a field 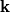 is
provided by the expansion near the unit of the multiplication map
is
provided by the expansion near the unit of the multiplication map
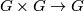 in a one-dimensional algebraic group over
in a one-dimensional algebraic group over 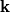 .
This also explains the terminology.
.
This also explains the terminology.
A formal group law  over
over  is called linearisable if
there exists a coordinate change
is called linearisable if
there exists a coordinate change ![u\mapsto g_F(u)=u+\sum_{i>0}g_iu^i\in R[[u]]](/images/math/4/0/2/402275b06df1121bd77c1e46f1b386dd.png) such that
such that
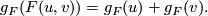
Note that every formal group law over  determines a formal
group law over
determines a formal
group law over  .
.
Theorem 2.1.
Every formal group law  is linearisable over
is linearisable over  .
.
Proof. Consider the series 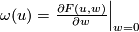 . Then
. Then
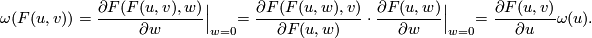
We therefore have
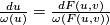 . Set
. Set
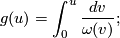
then 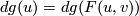 . This implies that
. This implies that 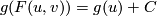 .
Since
.
Since 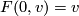 and
and 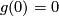 , we get
, we get 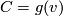 . Thus,
. Thus,
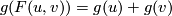 .
.
A series 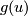 satisfying the equation
satisfying the equation 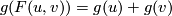 is called
the logarithm of the formal group law
is called
the logarithm of the formal group law  ; the above Theorem
shows that a formal group law over
; the above Theorem
shows that a formal group law over  always has a logarithm. Its functional inverse series
always has a logarithm. Its functional inverse series
![f(t)\in R\otimes\mathbb Q[[t]]](/images/math/d/8/d/d8df1357c59114c6756e554a41d3d2cb.png) is called the exponential of
the formal group law, so that we have
is called the exponential of
the formal group law, so that we have 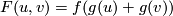 over
over  . If
. If  does not have torsion (i.e.
does not have torsion (i.e. 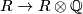 is monic), the latter formula shows that a formal group law (as a series with coefficients in
is monic), the latter formula shows that a formal group law (as a series with coefficients in  ) is fully
determined by its logarithm (which is a series with coefficients in
) is fully
determined by its logarithm (which is a series with coefficients in  ).
).
Let 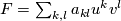 be a formal group law over a ring
be a formal group law over a ring
 and
and 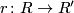 a ring homomorphism. Denote by
a ring homomorphism. Denote by 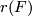 the formal series
the formal series ![\sum_{k,l}r(a_{kl})u^kv^l\in R'[[u,v]]](/images/math/7/9/f/79f6c5bbdc00bf4b92d352b3ad689c32.png) ; then
; then
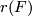 is a formal group law over
is a formal group law over 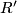 .
.
A formal group law  over a ring
over a ring  is universal if
for any formal group law
is universal if
for any formal group law  over any ring
over any ring  there exists a
unique homomorphism
there exists a
unique homomorphism 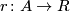 such that
such that 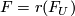 .
.
Proposition 2.2.
Assume that the universal formal group law  over
over  exists.
Then
exists.
Then
- The ring
 is multiplicatively generated by the coefficients of the series
is multiplicatively generated by the coefficients of the series  ;
;
- The universal formal group law is unique: if
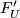 is another universal formal group law over
is another universal formal group law over 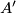 , then there is an isomorphism
, then there is an isomorphism 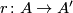 such that
such that 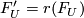 .
.
Proof. To prove the first statement, denote by 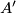 the subring in
the subring in  generated by the coefficients of
generated by the coefficients of  . Then there is a
monomorphism
. Then there is a
monomorphism 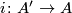 satisfying
satisfying 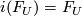 . On the
other hand, by universality there exists a homomorphism
. On the
other hand, by universality there exists a homomorphism 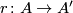 satisfying
satisfying 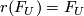 . It follows that
. It follows that 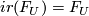 .
This implies that
.
This implies that 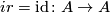 by the uniqueness
requirement in the definition of
by the uniqueness
requirement in the definition of  . Thus
. Thus 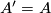 . The second
statement is proved similarly.
. The second
statement is proved similarly.
Theorem 2.3 ([Lazard1955]).
The universal formal group law  exists, and its coefficient
ring
exists, and its coefficient
ring  is isomorphic to the polynomial ring
is isomorphic to the polynomial ring ![\mathbb Z[a_1,a_2,\ldots]](/images/math/8/2/c/82c9310fe354b92a2a7693849d745f6e.png) on an infinite number of generators.
on an infinite number of generators.
3 Formal group law of geometric cobordisms
4 Hirzebruch genera
5 References
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Lazard1955] M. Lazard, Sur les groupes de Lie formels à un paramètre, Bull. Soc. Math. France 83 (1955), 251–274. MR0073925 (17,508e) Zbl 0068.25703
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
|
This page has not been refereed. The information given here might be incomplete or provisional. |
A formal power series ![F(u,v)\in R[[u,v]]](/images/math/7/4/f/74f4f62ad66dd8d43f3631de0acc5087.png) is called a
(commutative one-dimensional) formal group law over
is called a
(commutative one-dimensional) formal group law over  if
it satisfies the following equations:
if
it satisfies the following equations:
-
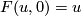 ,
, 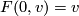 ;
;
-
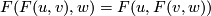 ;
;
-
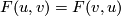 .
.
The original example of a formal group law over a field 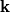 is
provided by the expansion near the unit of the multiplication map
is
provided by the expansion near the unit of the multiplication map
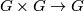 in a one-dimensional algebraic group over
in a one-dimensional algebraic group over 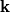 .
This also explains the terminology.
.
This also explains the terminology.
A formal group law  over
over  is called linearisable if
there exists a coordinate change
is called linearisable if
there exists a coordinate change ![u\mapsto g_F(u)=u+\sum_{i>0}g_iu^i\in R[[u]]](/images/math/4/0/2/402275b06df1121bd77c1e46f1b386dd.png) such that
such that
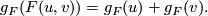
Note that every formal group law over  determines a formal
group law over
determines a formal
group law over  .
.
Theorem 2.1.
Every formal group law  is linearisable over
is linearisable over  .
.
Proof. Consider the series 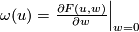 . Then
. Then
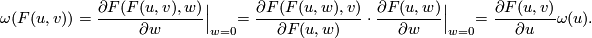
We therefore have
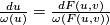 . Set
. Set
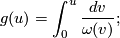
then 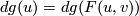 . This implies that
. This implies that 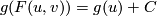 .
Since
.
Since 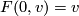 and
and 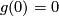 , we get
, we get 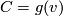 . Thus,
. Thus,
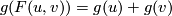 .
.
A series 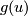 satisfying the equation
satisfying the equation 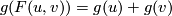 is called
the logarithm of the formal group law
is called
the logarithm of the formal group law  ; the above Theorem
shows that a formal group law over
; the above Theorem
shows that a formal group law over  always has a logarithm. Its functional inverse series
always has a logarithm. Its functional inverse series
![f(t)\in R\otimes\mathbb Q[[t]]](/images/math/d/8/d/d8df1357c59114c6756e554a41d3d2cb.png) is called the exponential of
the formal group law, so that we have
is called the exponential of
the formal group law, so that we have 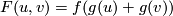 over
over  . If
. If  does not have torsion (i.e.
does not have torsion (i.e. 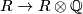 is monic), the latter formula shows that a formal group law (as a series with coefficients in
is monic), the latter formula shows that a formal group law (as a series with coefficients in  ) is fully
determined by its logarithm (which is a series with coefficients in
) is fully
determined by its logarithm (which is a series with coefficients in  ).
).
Let 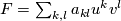 be a formal group law over a ring
be a formal group law over a ring
 and
and 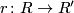 a ring homomorphism. Denote by
a ring homomorphism. Denote by 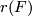 the formal series
the formal series ![\sum_{k,l}r(a_{kl})u^kv^l\in R'[[u,v]]](/images/math/7/9/f/79f6c5bbdc00bf4b92d352b3ad689c32.png) ; then
; then
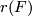 is a formal group law over
is a formal group law over 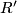 .
.
A formal group law  over a ring
over a ring  is universal if
for any formal group law
is universal if
for any formal group law  over any ring
over any ring  there exists a
unique homomorphism
there exists a
unique homomorphism 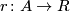 such that
such that 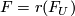 .
.
Proposition 2.2.
Assume that the universal formal group law  over
over  exists.
Then
exists.
Then
- The ring
 is multiplicatively generated by the coefficients of the series
is multiplicatively generated by the coefficients of the series  ;
;
- The universal formal group law is unique: if
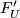 is another universal formal group law over
is another universal formal group law over 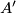 , then there is an isomorphism
, then there is an isomorphism 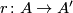 such that
such that 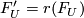 .
.
Proof. To prove the first statement, denote by 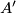 the subring in
the subring in  generated by the coefficients of
generated by the coefficients of  . Then there is a
monomorphism
. Then there is a
monomorphism 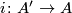 satisfying
satisfying 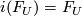 . On the
other hand, by universality there exists a homomorphism
. On the
other hand, by universality there exists a homomorphism 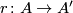 satisfying
satisfying 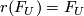 . It follows that
. It follows that 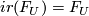 .
This implies that
.
This implies that 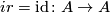 by the uniqueness
requirement in the definition of
by the uniqueness
requirement in the definition of  . Thus
. Thus 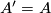 . The second
statement is proved similarly.
. The second
statement is proved similarly.
Theorem 2.3 ([Lazard1955]).
The universal formal group law  exists, and its coefficient
ring
exists, and its coefficient
ring  is isomorphic to the polynomial ring
is isomorphic to the polynomial ring ![\mathbb Z[a_1,a_2,\ldots]](/images/math/8/2/c/82c9310fe354b92a2a7693849d745f6e.png) on an infinite number of generators.
on an infinite number of generators.
3 Formal group law of geometric cobordisms
4 Hirzebruch genera
5 References
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Lazard1955] M. Lazard, Sur les groupes de Lie formels à un paramètre, Bull. Soc. Math. France 83 (1955), 251–274. MR0073925 (17,508e) Zbl 0068.25703
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
|
This page has not been refereed. The information given here might be incomplete or provisional. |
A formal power series ![F(u,v)\in R[[u,v]]](/images/math/7/4/f/74f4f62ad66dd8d43f3631de0acc5087.png) is called a
(commutative one-dimensional) formal group law over
is called a
(commutative one-dimensional) formal group law over  if
it satisfies the following equations:
if
it satisfies the following equations:
-
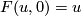 ,
, 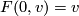 ;
;
-
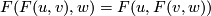 ;
;
-
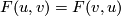 .
.
The original example of a formal group law over a field 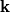 is
provided by the expansion near the unit of the multiplication map
is
provided by the expansion near the unit of the multiplication map
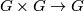 in a one-dimensional algebraic group over
in a one-dimensional algebraic group over 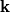 .
This also explains the terminology.
.
This also explains the terminology.
A formal group law  over
over  is called linearisable if
there exists a coordinate change
is called linearisable if
there exists a coordinate change ![u\mapsto g_F(u)=u+\sum_{i>0}g_iu^i\in R[[u]]](/images/math/4/0/2/402275b06df1121bd77c1e46f1b386dd.png) such that
such that
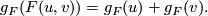
Note that every formal group law over  determines a formal
group law over
determines a formal
group law over  .
.
Theorem 2.1.
Every formal group law  is linearisable over
is linearisable over  .
.
Proof. Consider the series 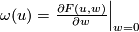 . Then
. Then
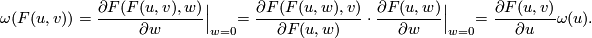
We therefore have
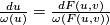 . Set
. Set
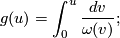
then 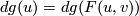 . This implies that
. This implies that 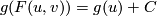 .
Since
.
Since 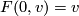 and
and 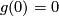 , we get
, we get 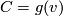 . Thus,
. Thus,
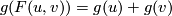 .
.
A series 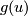 satisfying the equation
satisfying the equation 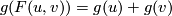 is called
the logarithm of the formal group law
is called
the logarithm of the formal group law  ; the above Theorem
shows that a formal group law over
; the above Theorem
shows that a formal group law over  always has a logarithm. Its functional inverse series
always has a logarithm. Its functional inverse series
![f(t)\in R\otimes\mathbb Q[[t]]](/images/math/d/8/d/d8df1357c59114c6756e554a41d3d2cb.png) is called the exponential of
the formal group law, so that we have
is called the exponential of
the formal group law, so that we have 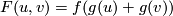 over
over  . If
. If  does not have torsion (i.e.
does not have torsion (i.e. 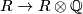 is monic), the latter formula shows that a formal group law (as a series with coefficients in
is monic), the latter formula shows that a formal group law (as a series with coefficients in  ) is fully
determined by its logarithm (which is a series with coefficients in
) is fully
determined by its logarithm (which is a series with coefficients in  ).
).
Let 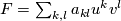 be a formal group law over a ring
be a formal group law over a ring
 and
and 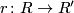 a ring homomorphism. Denote by
a ring homomorphism. Denote by 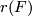 the formal series
the formal series ![\sum_{k,l}r(a_{kl})u^kv^l\in R'[[u,v]]](/images/math/7/9/f/79f6c5bbdc00bf4b92d352b3ad689c32.png) ; then
; then
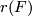 is a formal group law over
is a formal group law over 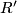 .
.
A formal group law  over a ring
over a ring  is universal if
for any formal group law
is universal if
for any formal group law  over any ring
over any ring  there exists a
unique homomorphism
there exists a
unique homomorphism 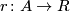 such that
such that 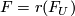 .
.
Proposition 2.2.
Assume that the universal formal group law  over
over  exists.
Then
exists.
Then
- The ring
 is multiplicatively generated by the coefficients of the series
is multiplicatively generated by the coefficients of the series  ;
;
- The universal formal group law is unique: if
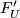 is another universal formal group law over
is another universal formal group law over 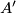 , then there is an isomorphism
, then there is an isomorphism 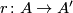 such that
such that 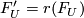 .
.
Proof. To prove the first statement, denote by 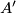 the subring in
the subring in  generated by the coefficients of
generated by the coefficients of  . Then there is a
monomorphism
. Then there is a
monomorphism 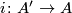 satisfying
satisfying 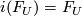 . On the
other hand, by universality there exists a homomorphism
. On the
other hand, by universality there exists a homomorphism 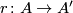 satisfying
satisfying 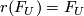 . It follows that
. It follows that 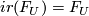 .
This implies that
.
This implies that 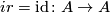 by the uniqueness
requirement in the definition of
by the uniqueness
requirement in the definition of  . Thus
. Thus 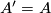 . The second
statement is proved similarly.
. The second
statement is proved similarly.
Theorem 2.3 ([Lazard1955]).
The universal formal group law  exists, and its coefficient
ring
exists, and its coefficient
ring  is isomorphic to the polynomial ring
is isomorphic to the polynomial ring ![\mathbb Z[a_1,a_2,\ldots]](/images/math/8/2/c/82c9310fe354b92a2a7693849d745f6e.png) on an infinite number of generators.
on an infinite number of generators.
3 Formal group law of geometric cobordisms
4 Hirzebruch genera
5 References
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Lazard1955] M. Lazard, Sur les groupes de Lie formels à un paramètre, Bull. Soc. Math. France 83 (1955), 251–274. MR0073925 (17,508e) Zbl 0068.25703
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
|
This page has not been refereed. The information given here might be incomplete or provisional. |