Even dimensional surgery obstruction (Ex)
(Difference between revisions)
Patrickorson (Talk | contribs) |
Patrickorson (Talk | contribs) |
||
| Line 4: | Line 4: | ||
# Show that any closed, orientable $m$-manifold $M^m$, possesses a degree 1 map $f:M^m\to S^m$. | # Show that any closed, orientable $m$-manifold $M^m$, possesses a degree 1 map $f:M^m\to S^m$. | ||
# For $m=2$ and $M$ the torus, find all degree 1 normal maps $(\bar{f},f)$ that cover $f$. | # For $m=2$ and $M$ the torus, find all degree 1 normal maps $(\bar{f},f)$ that cover $f$. | ||
| − | # For each of the $(\bar{f},f)$, calculate the surgery obstruction $\sigma_*(\bar{f},f)\in L_2(\mathbb{Z})$. If this vanishes, write down an explicit surgery on $(\bar{f},f)$ that describes a | + | # For each of the $(\bar{f},f)$, calculate the surgery obstruction $\sigma_*(\bar{f},f)\in L_2(\mathbb{Z})$. If this vanishes, write down an explicit surgery on $(\bar{f},f)$ that describes a cobordism of the torus to the 2-sphere. |
| − | Note if there is surgery obstruction that even though we know the torus is | + | Note if there is surgery obstruction that even though we know the torus is cobordant to the 2-sphere, the wrong normal map in the surgery programme will not find this nullcobordism. |
</wikitex> | </wikitex> | ||
Revision as of 23:39, 19 March 2012
This question is intended to illustrate the importance of the normal map in defining the even-dimensional surgery obstruction.
- Show that any closed, orientable
 -manifold
-manifold 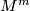 , possesses a degree 1 map
, possesses a degree 1 map 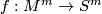 .
.
- For
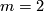 and
and  the torus, find all degree 1 normal maps
the torus, find all degree 1 normal maps 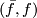 that cover
that cover  .
.
- For each of the
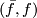 , calculate the surgery obstruction
, calculate the surgery obstruction 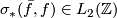 . If this vanishes, write down an explicit surgery on
. If this vanishes, write down an explicit surgery on 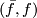 that describes a cobordism of the torus to the 2-sphere.
that describes a cobordism of the torus to the 2-sphere.
Note if there is surgery obstruction that even though we know the torus is cobordant to the 2-sphere, the wrong normal map in the surgery programme will not find this nullcobordism.