Even dimensional surgery obstruction (Ex)
(Difference between revisions)
Patrickorson (Talk | contribs) |
Patrickorson (Talk | contribs) |
||
| Line 6: | Line 6: | ||
# For each of the $(\bar{f},f)$, calculate the surgery obstruction $\sigma_*(\bar{f},f)\in L_2(\mathbb{Z})$. If this vanishes, write down an explicit surgery on $(\bar{f},f)$ that describes a nullcobordism of the torus. | # For each of the $(\bar{f},f)$, calculate the surgery obstruction $\sigma_*(\bar{f},f)\in L_2(\mathbb{Z})$. If this vanishes, write down an explicit surgery on $(\bar{f},f)$ that describes a nullcobordism of the torus. | ||
| − | Note | + | Note if there is surgery obstruction that even though we know the torus is nullcobordant, the wrong normal map in the surgery programme will not find this nullcobordism. |
</wikitex> | </wikitex> | ||
Revision as of 23:31, 19 March 2012
This question is intended to illustrate the importance of the normal map in defining the even-dimensional surgery obstruction.
- Show that any closed, orientable
 -manifold
-manifold 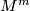 , possesses a degree 1 map
, possesses a degree 1 map 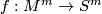 .
.
- For
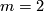 and
and  the torus, find all degree 1 normal maps
the torus, find all degree 1 normal maps 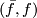 that cover
that cover  .
.
- For each of the
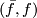 , calculate the surgery obstruction
, calculate the surgery obstruction 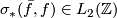 . If this vanishes, write down an explicit surgery on
. If this vanishes, write down an explicit surgery on 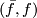 that describes a nullcobordism of the torus.
that describes a nullcobordism of the torus.
Note if there is surgery obstruction that even though we know the torus is nullcobordant, the wrong normal map in the surgery programme will not find this nullcobordism.