Equivariant intersection number of π-trivial immersions
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
This is a work in progress! Initial blurb.
Let 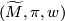 be an oriented cover of a connected manifold
be an oriented cover of a connected manifold 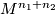 and let
and let 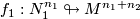 ,
, 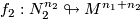 be
be  -trivial immersions of manifolds in
-trivial immersions of manifolds in  . The equivariant intersection number
. The equivariant intersection number ![\lambda([N_1],[N_2])\in\Z[\pi]](/images/math/b/c/d/bcdfc6dc4b56e4b2b7b24ca843038bd8.png) counts with elements of
counts with elements of ![\Z[\pi]](/images/math/1/e/c/1ecba37f7392a1697efda3ee93c740e2.png) the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint, which when zero can often be achieved using the Whitney trick.
the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint, which when zero can often be achieved using the Whitney trick.
The intersection number is also used in defining the intersection form of a  -dimensional manifold and in turn its signature - a very important invariant used in the classification of manifolds and the primary surgery obstruction.
-dimensional manifold and in turn its signature - a very important invariant used in the classification of manifolds and the primary surgery obstruction.
2 Definition
 with respect to an oriented cover
with respect to an oriented cover 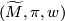
![\displaystyle \begin{array}{rcl}\lambda: H_n(\widetilde{M})\times H_{m-n}(\widetilde{M}) &\to& \Z[\pi]\\ (a,b) &\mapsto& \lambda(a,b)\end{array}](/images/math/0/b/4/0b4b53e55cd8acf4980d2c5535ca1469.png)
![\displaystyle \lambda(a,b) = a^*(b)\in \Z[\pi]](/images/math/b/0/f/b0fcae216fdc9e5f0f4c0c3575d15bcd.png)
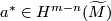 the Poincaré dual of
the Poincaré dual of  with respect to Universal Poincaré duality, such that
with respect to Universal Poincaré duality, such that ![\displaystyle \lambda(b,a) = (-1)^{n(m-n)}\overline{\lambda(a,b)}\in \Z[\pi].](/images/math/7/a/9/7a959480e00e19774331363df44ca591.png)
 -trivial maps
-trivial maps 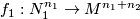 ,
, 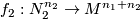 with prescribed lifts
with prescribed lifts 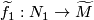 ,
, 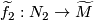 is the homology intersection of the homology classes
is the homology intersection of the homology classes ![(\widetilde{f}_1)_*[N_1]\in H_{n_1}(\widetilde{M})](/images/math/c/4/6/c46e32560c8615e67d873ca8c7ff648d.png) ,
, ![(\widetilde{f}_2)_*[N_2]\in H_{n_2}(\widetilde{M})](/images/math/1/f/e/1febc73b71c95f1718e9acbbff3df2c1.png) :
: ![\displaystyle \lambda^{\mathrm{alg}}(N_1,N_2) = \lambda((\widetilde{f}_1)_*[N_1],(\widetilde{f}_2)_*[N_2])\in \Z[\pi].](/images/math/0/a/5/0a5d108cbbc13596efbbc744b332d2cd.png)
3 Alternative Descriptions
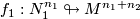 ,
, 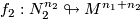 be
be  -trivial immersions. Let
-trivial immersions. Let 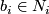 ,
, 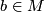 and
and 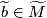 such that
such that 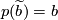 be basepoints. Then there is a bijective correspondence
be basepoints. Then there is a bijective correspondence 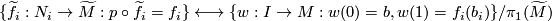
 -trivial maps. Thus there are two equivalent conventions we can use for the data of a
-trivial maps. Thus there are two equivalent conventions we can use for the data of a  -trivial map: either a choice of lift or a choice of path from
-trivial map: either a choice of lift or a choice of path from  to
to 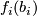 modulo
modulo 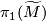 . Both conventions have equivalent definitions for the equivariant intersection number of transversely intersecting
. Both conventions have equivalent definitions for the equivariant intersection number of transversely intersecting  -trivial immersions.
-trivial immersions.
Lifts:
Let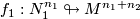 ,
, 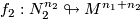 be
be  -trivial immersions with prescribed lifts to the oriented cover
-trivial immersions with prescribed lifts to the oriented cover 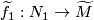 ,
, 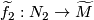 . At a transverse double point
. At a transverse double point 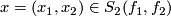 let
let 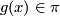 be the unique covering translation
be the unique covering translation 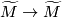 such that
such that 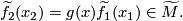
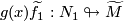 ,
, 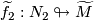 have a transverse double point
have a transverse double point 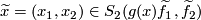
 -dimensional vector spaces
-dimensional vector spaces 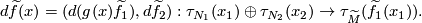
![I(x)\in\Z[\pi]](/images/math/5/f/f/5ffce5e793f9e8c62ad8efee6f130718.png) of a transverse double point
of a transverse double point 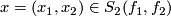 is
is ![\displaystyle I(x) = w(x)g(x)\in{\pm\pi}\subset \Z[\pi]](/images/math/1/a/c/1acb377eeb39fd20abd919a8e9be5b55.png)
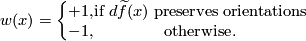
Paths:
Let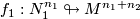 ,
, 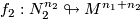 be
be  -trivial immersions with prescribed equivalence classes of paths
-trivial immersions with prescribed equivalence classes of paths ![[w_i:I\to M]](/images/math/6/0/2/60250747a77973d74f7dd12ff5dac28d.png) such that
such that 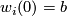 and
and 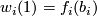 for
for 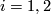 . At a transverse double point
. At a transverse double point 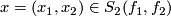 define
define 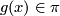 as the loop
as the loop 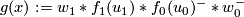
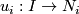 is any path from
is any path from 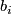 to
to 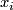 . This loop is well-defined since a different choice of representative of
. This loop is well-defined since a different choice of representative of 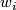 or a different path
or a different path 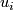 results in a loop that differs from the other by an element of
results in a loop that differs from the other by an element of 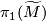 or
or 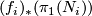 which is trivial in
which is trivial in  .
.
Definition of 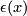 :
:
Equivalence:
Let  be a basepoint of
be a basepoint of  ,
, 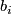 a basepoint of
a basepoint of 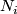 for
for 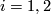 and let
and let 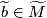 be some choice of lift. For a transverse double point
be some choice of lift. For a transverse double point 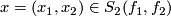 , an isotopy class of paths from
, an isotopy class of paths from 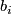 to
to 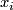 corresponds to a lift
corresponds to a lift 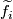 as follows.
as follows.
![\displaystyle I(x_2,x_1) = (-1)^{n_1n_2}\overline{I(x_1,x_2)}\in\Z[\pi]](/images/math/a/e/d/aede0071954c04f02bad98282381d414.png)
![\Z[\pi]\to \Z[\pi];a \mapsto \overline{a}](/images/math/a/8/7/a8741f19d2532c7dba3b6941e56c3b69.png) the
the  -twisted involution
-twisted involution 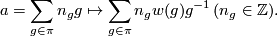
The geometric intersection number of transverse immersions 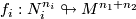
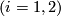 is
is
![\displaystyle \lambda^{\mathrm{geo}}(N_1,N_2) = \sum_{x\in S_2(f_1,f_2)}{I(x)}\in \Z[\pi].](/images/math/1/d/1/1d191be0a6f9a0c566a9030f40a3ea2a.png)
4 Equivalence of definitions
The algebraic and geometric intersection numbers agree. See REFERENCE
5 Examples
...