Equivariant intersection number of π-trivial immersions
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
This is a work in progress! Initial blurb.
Let 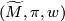 be an oriented cover of a connected manifold
be an oriented cover of a connected manifold 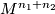 and let
and let 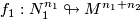 ,
, 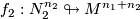 be
be  -trivial immersions of manifolds in
-trivial immersions of manifolds in  . The equivariant intersection number
. The equivariant intersection number ![\lambda([N_1],[N_2])\in\Z[\pi]](/images/math/b/c/d/bcdfc6dc4b56e4b2b7b24ca843038bd8.png) counts with elements of
counts with elements of ![\Z[\pi]](/images/math/1/e/c/1ecba37f7392a1697efda3ee93c740e2.png) the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint, which when zero can often be achieved using the Whitney trick.
the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint, which when zero can often be achieved using the Whitney trick.
The intersection number is also used in defining the intersection form of a  -dimensional manifold and in turn its signature - a very important invariant used in the classification of manifolds and the primary surgery obstruction.
-dimensional manifold and in turn its signature - a very important invariant used in the classification of manifolds and the primary surgery obstruction.
[edit] 2 Definition
 with respect to an oriented cover
with respect to an oriented cover 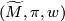
![\displaystyle \begin{array}{rcl}\lambda: H_n(\widetilde{M})\times H_{m-n}(\widetilde{M}) &\to& \Z[\pi]\\ (a,b) &\mapsto& \lambda(a,b)\end{array}](/images/math/0/b/4/0b4b53e55cd8acf4980d2c5535ca1469.png)
![\displaystyle \lambda(a,b) = a^*(b)\in \Z[\pi]](/images/math/b/0/f/b0fcae216fdc9e5f0f4c0c3575d15bcd.png)
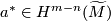 the Poincaré dual of
the Poincaré dual of  with respect to Universal Poincaré duality, such that
with respect to Universal Poincaré duality, such that ![\displaystyle \lambda(b,a) = (-1)^{n(m-n)}\overline{\lambda(a,b)}\in \Z[\pi].](/images/math/7/a/9/7a959480e00e19774331363df44ca591.png)
 -trivial maps
-trivial maps 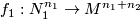 ,
, 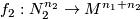 with prescribed lifts
with prescribed lifts 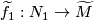 ,
, 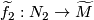 is the homology intersection of the homology classes
is the homology intersection of the homology classes ![(\widetilde{f}_1)_*[N_1]\in H_{n_1}(\widetilde{M})](/images/math/c/4/6/c46e32560c8615e67d873ca8c7ff648d.png) ,
, ![(\widetilde{f}_2)_*[N_2]\in H_{n_2}(\widetilde{M})](/images/math/1/f/e/1febc73b71c95f1718e9acbbff3df2c1.png) :
: ![\displaystyle \lambda^{\mathrm{alg}}(N_1,N_2) = \lambda((\widetilde{f}_1)_*[N_1],(\widetilde{f}_2)_*[N_2])\in \Z[\pi].](/images/math/0/a/5/0a5d108cbbc13596efbbc744b332d2cd.png)
[edit] 3 Alternative Description: Lifts
As in the non-equivariant case the equivariant intersection form has a geometric interpretation. Let 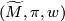 be an oriented cover of a connected manifold
be an oriented cover of a connected manifold 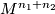 with
with  -twisted fundamental class
-twisted fundamental class ![[\widetilde{M}]\in H_{n_1+n_2}(M;\Z^w)](/images/math/7/5/4/754443c9bbb2af67b082b919cbd77201.png) corresponding to the lift
corresponding to the lift 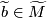 of the basepoint
of the basepoint 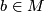 . Let
. Let 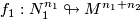 ,
, 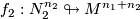 be transverse
be transverse  -trivial immersions of oriented manifolds with prescribed lifts
-trivial immersions of oriented manifolds with prescribed lifts 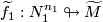 ,
, 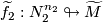 .
.
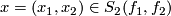 there is a unique covering translation
there is a unique covering translation 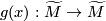 such that
such that 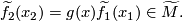
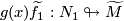 ,
, 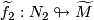 have a transverse double point
have a transverse double point 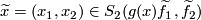
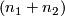 -dimensional vector spaces
-dimensional vector spaces 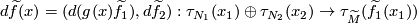
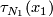 ,
, 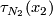 and
and 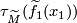 all inherit orientations from the given orientations of
all inherit orientations from the given orientations of 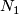 ,
, 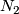 and
and  .
The equivariant index
.
The equivariant index ![I(x)=I(x_1,x_2)\in\Z[\pi]](/images/math/5/f/b/5fb6d0c9d0e9599764435c2cba0faf4a.png) of a transverse double point
of a transverse double point 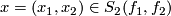 is defined to be
is defined to be ![\displaystyle I(x) = \epsilon(x)g(x)\in{\pm\pi}\subset \Z[\pi]](/images/math/f/2/d/f2df2770489968fbd580e4eda396a118.png)
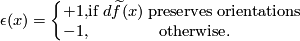
 and
and 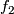 is then defined to be
is then defined to be ![\displaystyle \lambda_{\Z[\pi]}^{\mathrm{geo}}(f_1,f_2):= \sum_{x\in S_2(f_1,f_2)}{I(x)}\in \Z[\pi].](/images/math/d/3/e/d3ef600c38196816eeea0e2211cec383.png)
![\displaystyle I(x_2,x_1) = (-1)^{n_1n_2}\overline{I(x_1,x_2)}\in\Z[\pi]](/images/math/a/e/d/aede0071954c04f02bad98282381d414.png)
![\Z[\pi]\to \Z[\pi];a \mapsto \overline{a}](/images/math/a/8/7/a8741f19d2532c7dba3b6941e56c3b69.png) the
the  -twisted involution
-twisted involution 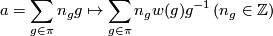
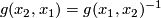 and the orientation of
and the orientation of 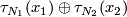 agrees with the orientation of
agrees with the orientation of 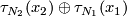 if and only if
if and only if 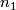 and
and 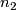 are not both odd. Consequently
are not both odd. Consequently ![\displaystyle \lambda_{\Z[\pi]}^{\mathrm{geo}}(f_2,f_1) = (-1)^{n_1n_2}\overline{\lambda_{\Z[\pi]}^{\mathrm{geo}}(f_1,f_2)}.](/images/math/a/8/f/a8f6f60c47afc1e8d68b70373795fe68.png)
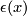 agrees with the non-equivariant index
agrees with the non-equivariant index 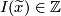 of the transverse double point
of the transverse double point 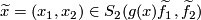 from which it follows that
from which it follows that ![\displaystyle \lambda_{\Z[\pi]}^{\mathrm{geo}}(f_1,f_2) = \sum_{g\in\pi}\lambda_{\Z}^{\mathrm{geo}}(g\widetilde{f}_1,\widetilde{f}_2)g\in \Z[\pi].](/images/math/2/7/d/27dd1648e043309d5177b8662ab2eab4.png)
[edit] 4 Alternative Description: Paths
 -trivial maps given basepoints
-trivial maps given basepoints 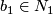 ,
, 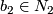 and
and 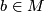 , a choice of lift,
, a choice of lift, 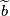 , of
, of  to the oriented cover
to the oriented cover  defines a bijection of sets
defines a bijection of sets 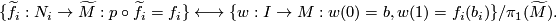
Thus there are two equivalent conventions for the data of a  -trivial map
-trivial map 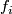 : either a choice of lift of
: either a choice of lift of 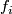 or the homotopy class of a choice of path from
or the homotopy class of a choice of path from  to
to 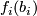 modulo
modulo 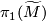 . In the previous section the geometric equivariant intersection number of
. In the previous section the geometric equivariant intersection number of  and
and 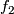 was defined using lifts as data. In this section we see the equivalent approach of using paths and prove the equivalence.
was defined using lifts as data. In this section we see the equivalent approach of using paths and prove the equivalence.
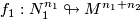 ,
, 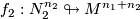 be
be  -trivial immersions with prescribed equivalence classes of paths
-trivial immersions with prescribed equivalence classes of paths ![[w_i:I\to M]](/images/math/6/0/2/60250747a77973d74f7dd12ff5dac28d.png) such that
such that 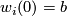 and
and 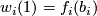 for
for 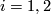 . At a transverse double point
. At a transverse double point 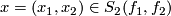 define
define 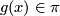 to be the class of the loop
to be the class of the loop ![\displaystyle g(x):= [w_1 * f_1(u_1) * f_0(u_0)^-*w_0^-]](/images/math/5/0/4/5043b1602135d3f3c7956b79972a5dfe.png)
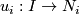 is any path from
is any path from 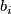 to
to 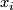 ,
, 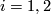 ,
, 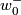 denotes the path
denotes the path 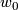 in reverse and
in reverse and  denotes concatenation of paths. This is well-defined since a different choice of representative of
denotes concatenation of paths. This is well-defined since a different choice of representative of 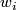 or a different path
or a different path 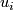 results in a loop that differs from the other by an element of
results in a loop that differs from the other by an element of 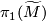 or
or 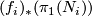 which is trivial in
which is trivial in  .
.
Definition of 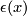 :
:
Equivalence:
Let  be a basepoint of
be a basepoint of  ,
, 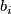 a basepoint of
a basepoint of 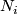 for
for 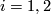 and let
and let 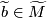 be some choice of lift. For a transverse double point
be some choice of lift. For a transverse double point 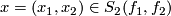 , an isotopy class of paths from
, an isotopy class of paths from 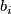 to
to 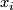 corresponds to a lift
corresponds to a lift 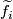 as follows.
as follows.
The geometric intersection number of transverse immersions 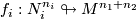
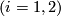 is
is
![\displaystyle \lambda^{\mathrm{geo}}(N_1,N_2) = \sum_{x\in S_2(f_1,f_2)}{I(x)}\in \Z[\pi].](/images/math/1/d/1/1d191be0a6f9a0c566a9030f40a3ea2a.png)
[edit] 5 Equivalence of definitions
The algebraic and geometric intersection numbers agree. See REFERENCE
[edit] 6 Examples
...