Curvature properties of exotic spheres

Revision as of 15:58, 7 June 2010

1 Introduction

This page is in the construction process!!!

A homotopy sphere of dimension $<!-- COMMENT: To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments: - For statements like Theorem, Lemma, Definition etc., use e.g. {{beginthm|Theorem 1|(Milnor)}} ... ... ... {{endthm}}. - For references, use e.g. {{cite|Milnor1958b}}. DON'T FORGET TO ENTER YOUR USER NAME INTO THE {{Authors| }} TEMPLATE BELOW. END OF COMMENT -->{{Authors|Joachim}} {{Stub}} == Introduction == <wikitex>; This page is in the construction process!!! A homotopy sphere of dimension $n$ is an oriented closed smooth manifold which is homotopy equivalent to the standard sphere $S^n$. A homotopy sphere is called an exotic sphere if it not diffeoemorphic to a standard sphere. General information about homotopy spheres (and exotic spheres) is given on [[Exotic spheres]]. One prominent question concerning the geometry of exotic spheres is: Given an exotic sphere, are there Riemannian metrics which fulfil specific positivity criteria? One typically considers the following three types. == Homotopy spheres with positive [[Wikipedia:Sectional_curvature|sectional curvature]] == == Homotopy spheres with positive [[Wikipedia:Ricci_curvature|Ricci curvature]] == == Homotopy spheres with positive [[Wikipedia:Scalar_curvature|scalar curvature]] == Hitchin (based on work of Lichnerowicz) proved that the so-called $\alpha$-$invariant$ of a closed spin manifold provides an obstruction to the existence of a metric of positive scalar curvature on it (cf. \cite{Hitchin1974}, \cite{Lichnerowicz1963}). The $\alpha$-invariant for a closed spin manifold (compare [[Spin bordism|Spin bordism Invariants]]) is given as follows: More information on the $\alpha$-invariant can be found at [[Spin In case $\dim(M)=1 \mod 8$ the space of harmonic spinors canonically has the structure of a complex vector space, while in case $\dim(M)=2 \mod 8$ the space of harmonic spinors canonically carries the structure of a quarternionic vector space. The $\alpha$-invariant of a homotopy sphere $\Sigma$ is given by $$ \alpha(\Sigma) = \left\{\begin{array}{lcl} \dim_{\Cc}Ker(D) \mod 2 && \text{if $\dim(\Sigma)= 1 \mod 8\ \dim_{\Hh}Ker(D) \mod 2 && \text{if $\dim(\Sigma)= 2 \mod 8\ 0 && in all other cases\right.$$ </wikitex> == References == {{#RefList:}} [[Category:Theory]]n$ is an oriented closed smooth manifold which is homotopy equivalent to the standard sphere $S^n$. A homotopy sphere is called an exotic sphere if it not diffeoemorphic to a standard sphere. General information about homotopy spheres (and exotic spheres) is given on Exotic spheres. One prominent question concerning the geometry of exotic spheres is: Given an exotic sphere, are there Riemannian metrics which fulfil specific positivity criteria? One typically considers the following three types.

1 Homotopy spheres with positive sectional curvature

2 Homotopy spheres with positive Ricci curvature

3 Homotopy spheres with positive scalar curvature

Hitchin (based on work of Lichnerowicz) proved that the so-called 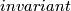$\alpha$-$invariant$ of a closed spin manifold provides an obstruction to the existence of a metric of positive scalar curvature on it (cf. [Hitchin1974], [Lichnerowicz1963]). The $\alpha$-invariant for a closed spin manifold (compare Spin bordism Invariants) is given as follows: More information on the $\alpha$-invariant can be found at [[Spin

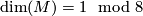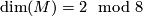In case $\dim(M)=1 \mod 8$ the space of harmonic spinors canonically has the structure of a complex vector space, while in case $\dim(M)=2 \mod 8$ the space of harmonic spinors canonically carries the structure of a quarternionic vector space.

The $\alpha$-invariant of a homotopy sphere $\Sigma$ is given by

Tex syntax error

2 References

• [Hitchin1974] N. Hitchin, Harmonic spinors, Advances in Math. 14 (1974), 1–55. MR0358873 (50 #11332) Zbl 0284.58016
• [Lichnerowicz1963] A. Lichnerowicz, Spineurs harmoniques, C. R. Acad. Sci. Paris 257 (1963), 7–9. MR0156292 (27 #6218) Zbl 0714.53041