Curvature properties of exotic spheres
|
The user responsible for this page is Joachim. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
This page is in the construction process!!!
A homotopy sphere of dimension  is an oriented closed smooth
manifold which is homotopy equivalent to the standard sphere
is an oriented closed smooth
manifold which is homotopy equivalent to the standard sphere  . A homotopy sphere is called an exotic sphere if it not diffeoemorphic to a standard sphere.
General information about homotopy spheres (and exotic spheres) is given on Exotic spheres. One prominent question concerning the geometry of exotic spheres is:
Given an exotic sphere, are there Riemannian metrics which fulfil specific positivity criteria? One typically considers the following three types.
. A homotopy sphere is called an exotic sphere if it not diffeoemorphic to a standard sphere.
General information about homotopy spheres (and exotic spheres) is given on Exotic spheres. One prominent question concerning the geometry of exotic spheres is:
Given an exotic sphere, are there Riemannian metrics which fulfil specific positivity criteria? One typically considers the following three types.
1 Homotopy spheres with positive sectional curvature
2 Homotopy spheres with positive Ricci curvature
3 Homotopy spheres with positive scalar curvature
Hitchin (based on results in [Lichnerowicz1963]) proved that the so-called  -invariant of a closed spin manifold provides an obstruction to the existence of a metric of positive scalar curvature on it (cf. [Hitchin1974]). The
-invariant of a closed spin manifold provides an obstruction to the existence of a metric of positive scalar curvature on it (cf. [Hitchin1974]). The  -invariant for a closed
-invariant for a closed  -dimensional spin manifold (compare Spin bordism Invariants) is given as follows: Let
-dimensional spin manifold (compare Spin bordism Invariants) is given as follows: Let 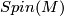 the principal
the principal 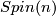 -bundle of
-bundle of  , and let
, and let  be obtained by adjoining the real Clifford algebra
be obtained by adjoining the real Clifford algebra 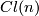 to
to 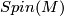 using the left multiplication of elements in
using the left multiplication of elements in 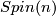 on
on 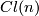 . The Dirac operator
. The Dirac operator 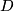 then acts on the space of sections
then acts on the space of sections 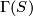 . The kernel of
. The kernel of 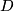 is called the space of (real) harmonic spinors. In case
is called the space of (real) harmonic spinors. In case 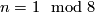 the space of harmonic spinors canonically has the structure of a complex vector space, while
in case
the space of harmonic spinors canonically has the structure of a complex vector space, while
in case 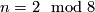 the space of harmonic spinors canonically carries the structure of a quarternionic vector space. The space of harmonic spinors determines an element in
the space of harmonic spinors canonically carries the structure of a quarternionic vector space. The space of harmonic spinors determines an element in 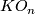 , the
, the  -invariant; and in particular, if the
-invariant; and in particular, if the  -invariant is non-trivial, the operator
-invariant is non-trivial, the operator 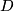 must have a non-trivial kernel.
must have a non-trivial kernel.
The  -invariant of a homotopy sphere can be computed explicitely by the following means; therefore note that
-invariant of a homotopy sphere can be computed explicitely by the following means; therefore note that 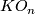 is isomorphic to
is isomorphic to 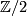 for
for 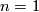 or
or 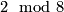 .
.
Proposition 7.1.
The  -invariant of a homotopy sphere
-invariant of a homotopy sphere  is given by
is given by
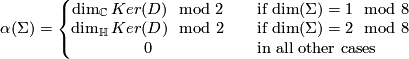
Theorem 7.2. Let  be an
be an  -dimensional homotopy sphere with
-dimensional homotopy sphere with 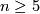 then
then  admits a metric of positive scalar curvature if and only if
admits a metric of positive scalar curvature if and only if 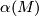 is trivial.
is trivial.
The fact that  -invariant is an obstruction to the existence of postive scalar curvature follows from the Bochner-Weitzenböck formula, which yields the formula
-invariant is an obstruction to the existence of postive scalar curvature follows from the Bochner-Weitzenböck formula, which yields the formula 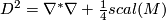 for the Dirac operator
for the Dirac operator 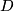 . Here
. Here 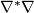 denotes the connection Laplacian which is a non-negative operator. Hence, if the scalar curature function
denotes the connection Laplacian which is a non-negative operator. Hence, if the scalar curature function 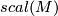 is strictly positive the operator
is strictly positive the operator 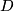 cannot have a non-trivial kernel, thus the
cannot have a non-trivial kernel, thus the  -invariant must be trivial.
-invariant must be trivial.
On the other hand, Stolz in [Stolz1992] proved that a simply connected closed spin manifold of dimension 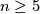 admits a metric of positive scalar curvature if its
admits a metric of positive scalar curvature if its  -invariant vanishes. The proof uses the surgery results for scalar curvature obtained (independently) in [Gromov&Lawson1980] and [Schoen&Yau1979], as well as a quite involved calculation within stable homotopy theory.
-invariant vanishes. The proof uses the surgery results for scalar curvature obtained (independently) in [Gromov&Lawson1980] and [Schoen&Yau1979], as well as a quite involved calculation within stable homotopy theory.
2 References
- [Gromov&Lawson1980] M. Gromov and H. B. Lawson, Spin and scalar curvature in the presence of a fundamental group. I, Ann. of Math. (2) 111 (1980), no.2, 209–230. MR569070 (81g:53022) Zbl 0445.53025
- [Hitchin1974] N. Hitchin, Harmonic spinors, Advances in Math. 14 (1974), 1–55. MR0358873 (50 #11332) Zbl 0284.58016
- [Lichnerowicz1963] A. Lichnerowicz, Spineurs harmoniques, C. R. Acad. Sci. Paris 257 (1963), 7–9. MR0156292 (27 #6218) Zbl 0714.53041
- [Schoen&Yau1979] R. Schoen and S. T. Yau, On the structure of manifolds with positive scalar curvature, Manuscripta Math. 28 (1979), no.1-3, 159–183. MR535700 (80k:53064) Zbl 0423.53032
- [Stolz1992] S. Stolz, Simply connected manifolds of positive scalar curvature, Ann. of Math. (2) 136 (1992), no.3, 511–540. MR1189863 (93i:57033) Zbl 0784.53029