Curvature properties of exotic spheres
| Line 33: | Line 33: | ||
More information on the $\alpah$-invariant can be found at [[Spin | More information on the $\alpah$-invariant can be found at [[Spin | ||
| − | In case $\dim(M)=1 \mod 8$ the space of harmonic spinors canonically has the structure of a complex vector space, while in case $\dim(M)=2 \mod 8$ the space of harmonic spinors canonically carries the structure of a quarternionic vector space. | + | In case $\dim(M)=1 \mod 8$ the space of harmonic spinors canonically has the structure of a complex vector space, while\\ |
| + | in case $\dim(M)=2 \mod 8$ the space of harmonic spinors canonically carries the structure of a quarternionic vector space. | ||
The $\alpha$-invariant of a homotopy sphere $\Sigma$ is given by | The $\alpha$-invariant of a homotopy sphere $\Sigma$ is given by | ||
Revision as of 14:54, 7 June 2010
|
The user responsible for this page is Joachim. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
This page is in the construction process!!!
A homotopy sphere of dimension  is an oriented closed smooth
manifold which is homotopy equivalent to the standard sphere
is an oriented closed smooth
manifold which is homotopy equivalent to the standard sphere  . A homotopy sphere is called an exotic sphere if it not diffeoemorphic to a standard sphere.
General information about homotopy spheres (and exotic spheres) is given on Exotic spheres. One prominent question concerning the geometry of exotic spheres is:
Given an exotic sphere, are there Riemannian metrics which fulfil specific positivity criteria? One typically considers the following three types.
. A homotopy sphere is called an exotic sphere if it not diffeoemorphic to a standard sphere.
General information about homotopy spheres (and exotic spheres) is given on Exotic spheres. One prominent question concerning the geometry of exotic spheres is:
Given an exotic sphere, are there Riemannian metrics which fulfil specific positivity criteria? One typically considers the following three types.
1 Homotopy spheres with positive sectional curvature
2 Homotopy spheres with positive Ricci curvature
3 Homotopy spheres with positive scalar curvature
Hitchin (based on work of Lichnerowicz) proved that the so-called  -invariant of a closed spin manifold provides an obstruction to the existence of a metric of positive scalar curvature on it. The
-invariant of a closed spin manifold provides an obstruction to the existence of a metric of positive scalar curvature on it. The  -invariant for a spin manifold is given as follows: ...
-invariant for a spin manifold is given as follows: ...
Tex syntax error-invariant can be found at [[Spin
In case 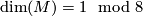 the space of harmonic spinors canonically has the structure of a complex vector space, while\\
in case
the space of harmonic spinors canonically has the structure of a complex vector space, while\\
in case 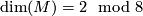 the space of harmonic spinors canonically carries the structure of a quarternionic vector space.
the space of harmonic spinors canonically carries the structure of a quarternionic vector space.
The  -invariant of a homotopy sphere
-invariant of a homotopy sphere  is given by
is given by
Tex syntax error