Complex bordism
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:39, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Taras Panov. No other user may edit this page at present. |
Contents |
1 Introduction
Complex bordisms (also known as unitary bordisms) is the bordism theory of stably complex manifolds. It is one of the most important theory of bordisms with additional structure, or B-bordisms.
The theory of complex bordisms is much richer than its unoriented analogue, and at the same time is not as complicated as oriented bordisms or other bordisms with additional structure (B-bordisms). Thanks to this, the complex cobordism theory found the most stricking and important applications in algebraic topology and beyond. Many of these applications, including the formal group techniques and Adams-Novikov spectral sequence were outlined in the pioneering work [Novikov1967].
2 Stably complex structures
A direct attempt to define the
bordism relation on complex manifolds fails because the manifold
 is odd-dimensional and therefore cannot be complex. In order to work with complex manifolds in the bordism theory, one needs to weaken the notion of the complex structures. This leads directly to considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) manifolds.
is odd-dimensional and therefore cannot be complex. In order to work with complex manifolds in the bordism theory, one needs to weaken the notion of the complex structures. This leads directly to considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) manifolds.
Let 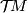 denote the tangent bundle of
denote the tangent bundle of  , and
, and 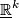 the product vector bundle
the product vector bundle 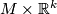 over
over  . A tangential stably complex structure on
. A tangential stably complex structure on  is
determined by a choice of an isomorphism
is
determined by a choice of an isomorphism
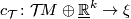
between the "stable" tangent bundle and a complex vector
bundle  over
over  . Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on
. Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on  is determined by a choice of a complex bundle
structure in the normal bundle
is determined by a choice of a complex bundle
structure in the normal bundle 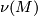 of an embedding
of an embedding
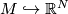 . A tangential and normal stably
complex structures on
. A tangential and normal stably
complex structures on  determine each other by means of the
canonical isomorphism
determine each other by means of the
canonical isomorphism 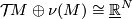 . We therefore may restrict
our attention to tangential structures only.
. We therefore may restrict
our attention to tangential structures only.
A stably complex manifold is a pair 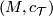 consisting of a manifold
consisting of a manifold  and a stably complex structure
and a stably complex structure
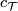 on it. This is a generalisation to a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on
on it. This is a generalisation to a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on 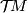 , i.e. a
stably complex structure
, i.e. a
stably complex structure 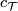 with
with 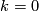 ).
).
Example 2.1.
Let 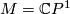 . The standard complex structure on
. The standard complex structure on  is
equivalent to a stably complex structure determined by the
isomorphism
is
equivalent to a stably complex structure determined by the
isomorphism
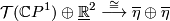
where 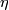 is the Hopf line bundle. On the other hand, the
isomorphism
is the Hopf line bundle. On the other hand, the
isomorphism
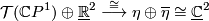
determines a trivial stably complex structure on 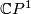 .
.
3 Definition of bordism and cobordism
The bordism relation can be defined between stably complex
manifolds. Like the case of unoriented bordisms, the set of
bordism classes ![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) of stably complex manifolds
is an Abelian group with respect to the disjoint union. This group
is called the group of
of stably complex manifolds
is an Abelian group with respect to the disjoint union. This group
is called the group of  -dimensional complex bordisms and
denoted
-dimensional complex bordisms and
denoted 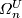 . A zero is represented by the bordism
class of any manifold
. A zero is represented by the bordism
class of any manifold  which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
vector bundle
which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
vector bundle 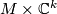 ). The sphere
). The sphere  provides an example
of such a manifold. The opposite element to the bordism class
provides an example
of such a manifold. The opposite element to the bordism class
![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) in the group
in the group 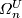 may be
represented by the same manifold
may be
represented by the same manifold  with the stably complex
structure determined by the isomorphism
with the stably complex
structure determined by the isomorphism
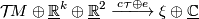
where 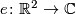 is given by
is given by 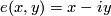 .
.
An abbreviated notation ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) for the complex
bordism class will be used whenever the stably complex structure
for the complex
bordism class will be used whenever the stably complex structure 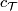 is clear from the context.
is clear from the context.
The groups of complex bordisms 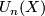 and cobordisms
and cobordisms 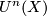 of a space
of a space  may also be defined
geometrically, at least for the case when
may also be defined
geometrically, at least for the case when  is a manifold. This can be done along the lines suggested by [Quillen1971] and [Dold1978] by considering special "stably complex" maps
of manifolds
is a manifold. This can be done along the lines suggested by [Quillen1971] and [Dold1978] by considering special "stably complex" maps
of manifolds  to
to  . However, nowadays the homotopical approach to
bordisms takes over, and the (co)bordism groups are usually
defined using the Pontrjagin-Thom construction similarly to the unoriented case:
. However, nowadays the homotopical approach to
bordisms takes over, and the (co)bordism groups are usually
defined using the Pontrjagin-Thom construction similarly to the unoriented case:
![\displaystyle \begin{aligned} U_n(X)&=\lim_{k\to\infty}\pi_{2k+n}((X_+)\wedge MU(k)),\\ U^n(X)&=\lim_{k\to\infty}[\Sigma^{2k-n}(X_+),MU(k)] \end{aligned}](/images/math/3/8/8/388203cfec203d491a8ba0f9062a963f.png)
where 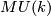 is the Thom space of the universal complex
is the Thom space of the universal complex  -plane
bundle
-plane
bundle 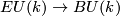 . These groups are
. These groups are 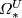 -modules
and give rise to a multiplicative (co)homology theory. In
particular,
-modules
and give rise to a multiplicative (co)homology theory. In
particular, 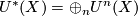 is a graded ring.
is a graded ring.
The graded
ring 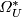 with
with 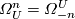 is
called the complex cobordism ring; it has nontrivial
elements only in nonpositively graded components.
is
called the complex cobordism ring; it has nontrivial
elements only in nonpositively graded components.
4 Geometric cobordisms
There is one important case when certain cobordism classes can be represented very explicitly by maps of manifolds.
For any cell complex the cohomology group
the cohomology group 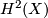 can be identified with the set
can be identified with the set Tex syntax errorof homotopy classes of
maps into 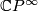 . Since
. Since 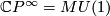 , every element
, every element 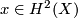 also determines
a cobordism class
also determines
a cobordism class 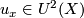 . The elements of
. The elements of 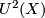 obtained in this way are called geometric cobordisms
of
obtained in this way are called geometric cobordisms
of  . We therefore may view
. We therefore may view 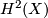 as a subset in
as a subset in 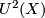 , however the group operation in
, however the group operation in 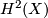 is not obtained by
restricting the group operation in
is not obtained by
restricting the group operation in 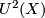 (see #Formal group laws and genera for the relationship
between the two operations).
(see #Formal group laws and genera for the relationship
between the two operations).
When  is a manifold, geometric cobordisms may be described by
submanifolds
is a manifold, geometric cobordisms may be described by
submanifolds  of codimension 2 with a fixed complex
structure in the normal bundle.
of codimension 2 with a fixed complex
structure in the normal bundle.
Indeed, every 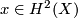 corresponds to a homotopy class of
maps
corresponds to a homotopy class of
maps 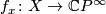 . The image
. The image 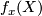 is contained
in some
is contained
in some 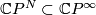 , and we may assume that
, and we may assume that
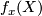 is transversal to a certain hyperplane
is transversal to a certain hyperplane 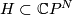 .
Then
.
Then 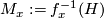 is a codimension 2 submanifold in
is a codimension 2 submanifold in  whose normal bundle acquires a complex structure by restriction of
the complex structure in the normal bundle of
whose normal bundle acquires a complex structure by restriction of
the complex structure in the normal bundle of 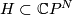 .
Changing the map
.
Changing the map 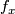 within its homotopy class does not affect
the bordism class of embedding
within its homotopy class does not affect
the bordism class of embedding 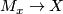 .
.
Conversely, assume given a submanifold  of codimension
2 whose normal bundle is endowed with a complex structure. Then
the composition
of codimension
2 whose normal bundle is endowed with a complex structure. Then
the composition
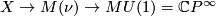
of the Pontrjagin-Thom collapse map 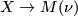 and the map of
Thom spaces corresponding the the classifying map
and the map of
Thom spaces corresponding the the classifying map 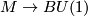 of
of  defines and element
defines and element 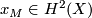 , and therefore a
geometric cobordism.
, and therefore a
geometric cobordism.
If  is an oriented manifold, then a choice of complex structure
in the normal bundle of a codimension 2 embedding
is an oriented manifold, then a choice of complex structure
in the normal bundle of a codimension 2 embedding  is
equivalent to orienting
is
equivalent to orienting  . The image of the fundamental class of
. The image of the fundamental class of
 in the homology of
in the homology of  is Poincar\'e dual to
is Poincar\'e dual to 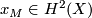 .
.
5 Structure results
6 Multiplicative generators
7 Formal group laws and genera
8 Adams-Novikov spectral sequence
The main references here are [Novikov1967] and [Ravenel1986]
9 References
- [Dold1978] A. Dold, Geometric cobordism and the fixed point transfer, in Algebraic topology (Proc. Conf., Univ. British Columbia, Vancouver, B.C., 1977), Lecture Notes in Math. 673, Springer, Berlin, (1978), 32–87. MR517084 (80g:57052) Zbl 0386.57005
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
- [Quillen1971] D. Quillen, The Adams conjecture, Topology 10 (1971), 67–80. MR0279804 (43 #5525) Zbl 0219.55013
- [Ravenel1986] D. C. Ravenel, Complex cobordism and stable homotopy groups of spheres, Academic Press Inc., Orlando, FL, 1986. MR860042 (87j:55003) Zbl 1073.55001
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
|
This page has not been refereed. The information given here might be incomplete or provisional. |