Complex bordism
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:39, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Taras Panov. No other user may edit this page at present. |
Contents |
1 Introduction
Complex bordisms (also known as unitary bordisms) is the bordism theory of stably complex manifolds. It is one of the most important theory of bordisms with additional structure, or B-bordisms.
The theory of complex bordisms is much richer than its unoriented analogue, and at the same time is not as complicated as oriented bordisms or other bordisms with additional structure (B-bordisms). Thanks to this, the complex cobordism theory found the most stricking and important applications in algebraic topology and beyond. Many of these applications, including the formal group techniques and Adams-Novikov spectral sequence were outlined in the pioneering work [Novikov1968].
2 Stably complex structures
A direct attempt to define the
bordism relation on complex manifolds fails because the manifold
 is odd-dimensional and therefore cannot be complex. In order to work with complex manifolds in the bordism theory, one needs to weaken the notion of the complex structures. This leads directly to considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) manifolds.
is odd-dimensional and therefore cannot be complex. In order to work with complex manifolds in the bordism theory, one needs to weaken the notion of the complex structures. This leads directly to considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) manifolds.
Let 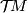 denote the tangent bundle of
denote the tangent bundle of  , and
, and 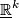 the product vector bundle
the product vector bundle 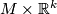 over
over  . A tangential stably complex structure on
. A tangential stably complex structure on  is
determined by a choice of an isomorphism
is
determined by a choice of an isomorphism
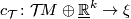
between the "stable" tangent bundle and a complex vector
bundle  over
over  . Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on
. Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on  is determined by a choice of a complex bundle
structure in the normal bundle
is determined by a choice of a complex bundle
structure in the normal bundle 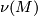 of an embedding
of an embedding
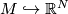 . A tangential and normal stably
complex structures on
. A tangential and normal stably
complex structures on  determine each other by means of the
canonical isomorphism
determine each other by means of the
canonical isomorphism 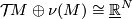 . We therefore may restrict
our attention to tangential structures only.
. We therefore may restrict
our attention to tangential structures only.
A stably complex manifold is a pair 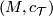 consisting of a manifold
consisting of a manifold  and a stably complex structure
and a stably complex structure
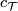 on it. This is a generalisation to a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on
on it. This is a generalisation to a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on 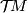 , i.e. a
stably complex structure
, i.e. a
stably complex structure 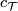 with
with 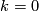 ).
).
Example 2.1.
Let 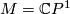 . The standard complex structure on
. The standard complex structure on  is
equivalent to a stably complex structure determined by the
isomorphism
is
equivalent to a stably complex structure determined by the
isomorphism
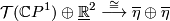
where 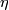 is the Hopf line bundle. On the other hand, the
isomorphism
is the Hopf line bundle. On the other hand, the
isomorphism
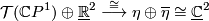
determines a trivial stably complex structure on 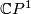 .
.
3 Definition of bordism and cobordism
4 Geometric cobordisms
5 Structure results
6 Multiplicative generators
7 Formal group laws and genera
8 Adams-Novikov spectral sequence
9 References
- [Novikov1968] Template:Novikov1968
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
|
This page has not been refereed. The information given here might be incomplete or provisional. |