Classifying spaces for families of subgroups
Contents |
1 Introduction
Given a discrete group  and a family of subgroups (see Definition 2.1 below)
and a family of subgroups (see Definition 2.1 below)  of
of  , there is a
, there is a  -CW complex,
-CW complex, 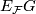 , that classifies
, that classifies  -CW complexes with isotropy contained in
-CW complexes with isotropy contained in  . That is, for every
. That is, for every  -CW complex
-CW complex  , there is a
, there is a  -equivariant map
-equivariant map 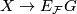 that is unique up to
that is unique up to  -equivariant homotopy. This universal property implies that
-equivariant homotopy. This universal property implies that 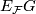 is unique up to
is unique up to  -homotopy. For this reason
-homotopy. For this reason 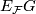 is known as the classifying space (or universal space) of
is known as the classifying space (or universal space) of  for the family
for the family  .
.
2 Construction and examples
Definition (Family of Subgroups) 2.1.
A family  of subgroups of a discrete group
of subgroups of a discrete group  is a collection of subgroups of
is a collection of subgroups of  that is closed under conjugation and taking subgroups.
that is closed under conjugation and taking subgroups.
Examples of families:
- The family containing only the trivial subgroup,
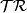 .
.
- The family of all subgroups,
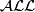 .
.
- The family of finite subgroups,
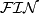 .
.
- The family of virtually cyclic subgroups,
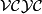 .
.
An important fact that follows from the Generalized Whitehead Theorem is:
Theorem 2.2.
Let 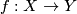 be a
be a  -equivariant map of
-equivariant map of  -CW complexes. Then
-CW complexes. Then  is a
is a  -equivariant homotopy equivalence if and only if for every subgroup
-equivariant homotopy equivalence if and only if for every subgroup  of
of  ,
, 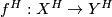 is a weak homotopy equivalence (i.e., induces an isomorphism on homotopy groups).
is a weak homotopy equivalence (i.e., induces an isomorphism on homotopy groups).
Theorem 2.2 implies that any two models for 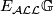 are
are  -equivariantly homotopy equivalent.
-equivariantly homotopy equivalent.
Examples of classifying spaces:
- A model for
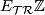 is
is 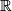 on which
on which  acts by translation.
acts by translation.
More generally, 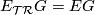 , the universal cover of the classifying space
, the universal cover of the classifying space 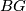 . (Recall that
. (Recall that 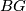 is a CW complex whose fundamental group is
is a CW complex whose fundamental group is  and whose higher homotopy groups are all zero. It is unique up to homotopy.)
and whose higher homotopy groups are all zero. It is unique up to homotopy.)
- For any
 ,
, 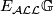 is
is  -equivariantly homotopy equivalent to a point.
-equivariantly homotopy equivalent to a point.
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |