Classifying spaces for families of subgroups
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 Introduction
Given a discrete group  and a family of subgroups
and a family of subgroups  of
of  (see Definition 2.2 below), there is a
(see Definition 2.2 below), there is a  -CW complex,
-CW complex, 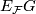 , that classifies
, that classifies  -CW complexes with isotropy contained in
-CW complexes with isotropy contained in  . That is, the isotropy subgroups of
. That is, the isotropy subgroups of 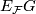 are contained in
are contained in  and for every
and for every  -CW complex
-CW complex  with isotropy in
with isotropy in  , there is a
, there is a  -equivariant map
-equivariant map 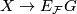 that is unique up to
that is unique up to  -equivariant homotopy. There can be many models for
-equivariant homotopy. There can be many models for 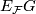 , but the universal property implies that they are all
, but the universal property implies that they are all  -homotopy equivalent. For this reason
-homotopy equivalent. For this reason 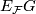 is known as the classifying space (or universal space) of
is known as the classifying space (or universal space) of  for the family
for the family  . A useful characterization of
. A useful characterization of 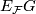 is given below (Corollary 2.5).
is given below (Corollary 2.5).
Classifying spaces for families of subgroups play an important role in the classification of manifolds with a given fundamental group  . The Farrell-Jones Conjecture relates the
. The Farrell-Jones Conjecture relates the  - and
- and  -theory of groups rings
-theory of groups rings 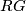 to certain equivariant homology theories evaluated at
to certain equivariant homology theories evaluated at 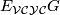 , the classifying space of
, the classifying space of  for the family of virtually cyclic subgroups. Similarly, the Baum-Connes Conjecture relates the topological
for the family of virtually cyclic subgroups. Similarly, the Baum-Connes Conjecture relates the topological  -theory of the reduced
-theory of the reduced 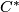 -algebra of
-algebra of  to an appropriate equivariant homology theory evaluated at
to an appropriate equivariant homology theory evaluated at 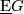 , the classifying space for proper
, the classifying space for proper  -actions. (In the case of a discrete group, this means that the isotropy is contained in the family of finite subgroups, i.e., all of the stabilizer subgroups are finite.) From the point of view of computations it is also important to find nice models for these spaces, and in particular for
-actions. (In the case of a discrete group, this means that the isotropy is contained in the family of finite subgroups, i.e., all of the stabilizer subgroups are finite.) From the point of view of computations it is also important to find nice models for these spaces, and in particular for 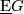 , since in many cases calculations can be reduced to working with the family of finite subgroups.
, since in many cases calculations can be reduced to working with the family of finite subgroups.
[edit] 2 Construction and examples
Definition ( -CW complex) 2.1.
A
-CW complex) 2.1.
A  -CW complex
-CW complex  is a
is a  -space with a
-space with a  -invariant filtration of spaces
-invariant filtration of spaces
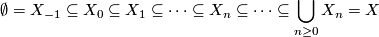
such that:
- a set
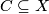 is closed if and only if
is closed if and only if 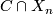 is closed for every
is closed for every 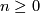 ;
;
- for each
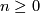 ,
, 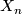 is obtained from
is obtained from 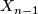 by attaching
by attaching  -dimensional
-dimensional  -cells. That is, there exists a
-cells. That is, there exists a  -pushout where
-pushout where![\displaystyle \xymatrix{ \coprod_{i \in I_n}G/H_i \times S^{n-1} \ar@{^{(}->}[d] \ar[r] & X_{n-1} \ar@{^{(}->}[d] \\ \coprod_{i \in I_n}G/H_i \times D^{n} \ar[r] & X }](/images/math/6/5/5/6550e0fc2a6bf66d4742de2482823080.png)
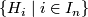 is a collection of subgroups of
is a collection of subgroups of  .
.
Examples
- The real line with the translation action of
 is a
is a  -CW complex with one equivariant
-CW complex with one equivariant  -cell (the integers) and one equivariant
-cell (the integers) and one equivariant  -cell (the orbit of the interval
-cell (the orbit of the interval ![[0,1]](/images/math/e/6/d/e6d5b5dafb82c2bf8b920a812188ac06.png) ).
).
-
 with the antipodal
with the antipodal 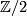 -action is a
-action is a 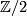 -CW complex with one equivariant
-CW complex with one equivariant  -cell for every
-cell for every  . (Notice that as a CW complex
. (Notice that as a CW complex  has two
has two  -cells for every
-cells for every  .)
.)
-
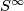 is a
is a 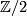 -CW complex with one equivariant
-CW complex with one equivariant  -cell in each dimension. The filtration is
-cell in each dimension. The filtration is 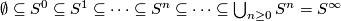 , with the antipodal action of
, with the antipodal action of 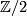 on each
on each  .
.
- Let
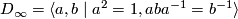 be the infinite dihedral group. It acts on
be the infinite dihedral group. It acts on 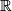 , where
, where  acts by reflection through zero and
acts by reflection through zero and  acts by translation by 1. Thus,
acts by translation by 1. Thus, 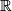 is a
is a 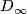 -CW complex with two equivariant
-CW complex with two equivariant  -cells (the orbits of 0 and
-cells (the orbits of 0 and 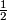 ) and one equivariant
) and one equivariant  -cell (the orbit of the interval
-cell (the orbit of the interval ![[0,\frac{1}{2}]](/images/math/0/6/c/06c139829b88c6f3512faea63478e2bc.png) ).
).
Definition (Family of subgroups) 2.2.
A family  of subgroups of a discrete group
of subgroups of a discrete group  is a collection of subgroups of
is a collection of subgroups of  that is closed under conjugation and taking subgroups.
that is closed under conjugation and taking subgroups.
Examples of families:
- The family containing only the trivial subgroup.
- The family of all subgroups.
- The family of finite subgroups,
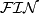 .
.
- The family of virtually cyclic subgroups,
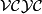 .
.
Definition (Classifying space for a family of subgroups) 2.3.
Let  be a family of subgroups of a discrete group
be a family of subgroups of a discrete group  . The classifying space of
. The classifying space of  for
for  is a
is a  -CW complex
-CW complex 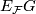 whose isotropy groups are contained in
whose isotropy groups are contained in  and has the property that for any
and has the property that for any  -CW complex
-CW complex  with isotropy in
with isotropy in  , there is a
, there is a  -equivariant map
-equivariant map 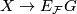 that is unique up to
that is unique up to  -homotopy.
-homotopy.
An important fact that follows from the Generalized Whitehead Theorem ([Lück2005, Theorem 1.6]) is:
Theorem 2.4.
Let 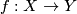 be a
be a  -equivariant map of
-equivariant map of  -CW complexes. Then
-CW complexes. Then  is a
is a  -homotopy equivalence if and only if for every subgroup
-homotopy equivalence if and only if for every subgroup  of
of  , the induced map on fixed sets
, the induced map on fixed sets 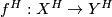 is a weak homotopy equivalence (i.e., induces an isomorphism on homotopy groups).
is a weak homotopy equivalence (i.e., induces an isomorphism on homotopy groups).
This gives us a way to determine whether or not a given  -CW complex is a model for
-CW complex is a model for 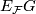 .
.
Corollary 2.5.
A  -CW complex
-CW complex  is a model for
is a model for 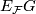 if and only if
if and only if 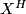 is weakly contractible for every
is weakly contractible for every 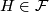 and is empty otherwise. In particular,
and is empty otherwise. In particular, 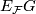 is contractible.
is contractible.
Examples
-
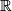 with the
with the  -CW structure described above is a model for the classifying space of
-CW structure described above is a model for the classifying space of  for the trivial family.
for the trivial family.
-
 with the
with the 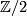 -CW structure described above is not a model for the classifying space of
-CW structure described above is not a model for the classifying space of 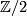 for the trivial family, because
for the trivial family, because  is not contractible.
is not contractible.
-
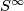 is a model for the classifying space of
is a model for the classifying space of 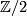 for the trivial family, since it is weakly contractible and hence contractible.
for the trivial family, since it is weakly contractible and hence contractible.
-
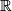 with the
with the 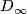 -CW structure described above is a model for the classifying space of
-CW structure described above is a model for the classifying space of 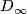 for the family of finite subgroups. Notice that the nontrivial finite subgroups of
for the family of finite subgroups. Notice that the nontrivial finite subgroups of 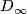 are of the form
are of the form 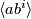 , where
, where 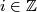 , and for each
, and for each  ,
, 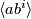 fixes
fixes 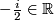 . All other points have trivial stabilizers.
. All other points have trivial stabilizers.
So far the existence question has been ignored. However, given a discrete group  and a family of subgroups
and a family of subgroups  of
of  , a model for
, a model for 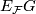 always exists. As explained in [Lück2005, Theorem 1.9], Corollary 2.5 implies that a model for
always exists. As explained in [Lück2005, Theorem 1.9], Corollary 2.5 implies that a model for 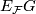 can be constructed by attaching equivariant
can be constructed by attaching equivariant  -cells,
-cells, 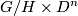 to kill each of the homotopy groups of the
to kill each of the homotopy groups of the  -fixed point sets, for each
-fixed point sets, for each  in
in  . This process is illustrated in the
. This process is illustrated in the 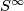 -example. Clearly, this procedure for constructing classifying spaces will typically produce very large models for
-example. Clearly, this procedure for constructing classifying spaces will typically produce very large models for 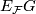 and is therefore usually not a useful model to work with.
and is therefore usually not a useful model to work with.
More examples of classifying spaces:
- The classifying space of
 for the trivial family (i.e., for free actions) is just
for the trivial family (i.e., for free actions) is just 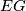 , the universal cover of the classifying space
, the universal cover of the classifying space 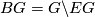 . (Recall that
. (Recall that 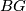 is a CW complex whose fundamental group is
is a CW complex whose fundamental group is  and whose higher homotopy groups are all zero; it is unique up to homotopy.)
and whose higher homotopy groups are all zero; it is unique up to homotopy.)
- For any group, a point is a model for the classifying space for the family of all subgroups.
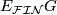 is also known as the classifying space (or universal space) for proper
is also known as the classifying space (or universal space) for proper  -actions, and is commonly written as
-actions, and is commonly written as 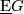 . There are typically "nice" models for
. There are typically "nice" models for 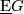 , as the
, as the 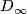 -example above and the next few examples show.
-example above and the next few examples show.
- Let
 be a discrete subgroup of a Lie group
be a discrete subgroup of a Lie group  with finitely many path components. If
with finitely many path components. If  is a maximal compact subgroup of
is a maximal compact subgroup of  , then
, then 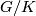 is a finite dimensional model for
is a finite dimensional model for 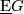 . ([Lück2005])
. ([Lück2005])
- Let
 be a word hyperbolic group in the sense of Gromov. Then the Rips complex,
be a word hyperbolic group in the sense of Gromov. Then the Rips complex, 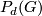 , is a finite model for
, is a finite model for 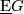 ( i.e., there are only finitely many
( i.e., there are only finitely many  -cells), provided
-cells), provided  is sufficiently large. ([Meintrup&Schick2002])
is sufficiently large. ([Meintrup&Schick2002])
- If
 is a
is a  -CW complex with the structure of a CAT(0)-space with respect to which
-CW complex with the structure of a CAT(0)-space with respect to which  acts by isometries, then
acts by isometries, then  is a model for
is a model for 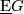 . ([Bridson&Haefliger1999])
. ([Bridson&Haefliger1999])
- Models for
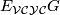 are hard to construct, but are needed in the formulation of the Farrell-Jones Conjecture.
are hard to construct, but are needed in the formulation of the Farrell-Jones Conjecture.
Classical sources on this topic are: [Bredon1967] [Bredon1972] [Tom Dieck1987]
[edit] 3 References
- [Bredon1967] G. E. Bredon, Equivariant cohomology theories, Lecture Notes in Mathematics, No. 34, Springer-Verlag, Berlin, 1967. MR0214062 (35 #4914) Zbl 0162.27202
- [Bredon1972] G. E. Bredon, Introduction to compact transformation groups, Academic Press, New York, 1972. MR0413144 (54 #1265) Zbl 0484.57001
- [Bridson&Haefliger1999] M. R. Bridson and A. Haefliger, Metric spaces of non-positive curvature, Springer-Verlag, Berlin, 1999. MR1744486 (2000k:53038) Zbl 0988.53001
- [Lück2005] W. Lück, Survey on classifying spaces for families of subgroups, Infinite groups: geometric, combinatorial and dynamical aspects, Progr. Math., 248, Birkhäuser, Basel (2005), 269–322. MR2195456 (2006m:55036) Zbl 1117.55013
- [Meintrup&Schick2002] D. Meintrup and T. Schick, A model for the universal space for proper actions of a hyperbolic group, New York J. Math. 8 (2002), 1–7 (electronic). MR1887695 (2003b:57002) Zbl 0990.20027
- [Tom Dieck1987] T. tom Dieck, Transformation groups, Walter de Gruyter & Co., Berlin, 1987. MR889050 (89c:57048) Zbl 0646.00011