Classifying spaces for families of subgroups
(Difference between revisions)
(→Introduction) |
(→Introduction) |
||
| Line 16: | Line 16: | ||
Given a discrete group $G$ and a ''family of subgroups'' (see Definition \ref{def:family} below) $\mathcal{F}$ of $G$, there is a $G$-CW complex, $E_\mathcal{F}G$, that classifies $G$-CW complexes with isotropy contained in $\mathcal{F}$. That is, for every $G$-CW complex $X$, there is a $G$-equivariant map $X \to E_\mathcal{F}G$ that is unique up to $G$-equivariant homotopy. This universal property implies that $E_\mathcal{F}G$ is unique up to $G$-homotopy. For this reason $E_\mathcal{F}G$ is known as the classifying space (or universal space) of $G$ for the family $\mathcal{F}$. | Given a discrete group $G$ and a ''family of subgroups'' (see Definition \ref{def:family} below) $\mathcal{F}$ of $G$, there is a $G$-CW complex, $E_\mathcal{F}G$, that classifies $G$-CW complexes with isotropy contained in $\mathcal{F}$. That is, for every $G$-CW complex $X$, there is a $G$-equivariant map $X \to E_\mathcal{F}G$ that is unique up to $G$-equivariant homotopy. This universal property implies that $E_\mathcal{F}G$ is unique up to $G$-homotopy. For this reason $E_\mathcal{F}G$ is known as the classifying space (or universal space) of $G$ for the family $\mathcal{F}$. | ||
| − | + | ||
| − | + | ||
| − | + | ||
</wikitex> | </wikitex> | ||
Revision as of 14:48, 7 June 2010
Contents |
1 Introduction
Given a discrete group  and a family of subgroups (see Definition \ref{def:family} below)
and a family of subgroups (see Definition \ref{def:family} below)  of
of  , there is a
, there is a  -CW complex,
-CW complex, 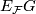 , that classifies
, that classifies  -CW complexes with isotropy contained in
-CW complexes with isotropy contained in  . That is, for every
. That is, for every  -CW complex
-CW complex  , there is a
, there is a  -equivariant map
-equivariant map 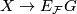 that is unique up to
that is unique up to  -equivariant homotopy. This universal property implies that
-equivariant homotopy. This universal property implies that 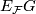 is unique up to
is unique up to  -homotopy. For this reason
-homotopy. For this reason 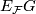 is known as the classifying space (or universal space) of
is known as the classifying space (or universal space) of  for the family
for the family  .
.
2 Construction and examples
...
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |