Chain duality I (Ex)
From Manifold Atlas
Revision as of 16:32, 1 June 2012 by Spiros Adams-Florou (Talk | contribs)
(i) Let 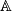 be an additive category and let
be an additive category and let 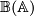 be the category of bounded chain complexes in
be the category of bounded chain complexes in 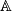 . Using the double complex extend
. Using the double complex extend  to a contravariant functor
to a contravariant functor

(ii) Suppose instead that 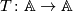 and that
and that 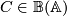 is concentrated between dimensions
is concentrated between dimensions  and
and  . Observe that the extension
. Observe that the extension 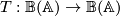 has
has 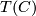 concentrated between dimensions
concentrated between dimensions  and
and 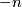 .
.
[edit] References
$ and $n$. Observe that the extension $T: \Bb(\Aa) \to \Bb(\Aa)$ has $T(C)$ concentrated between dimensions be an additive category and let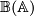 be the category of bounded chain complexes in
be the category of bounded chain complexes in 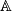 . Using the double complex extend
. Using the double complex extend  to a contravariant functor
to a contravariant functor

(ii) Suppose instead that 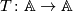 and that
and that 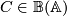 is concentrated between dimensions
is concentrated between dimensions  and
and  . Observe that the extension
. Observe that the extension 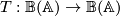 has
has 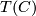 concentrated between dimensions
concentrated between dimensions  and
and 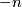 .
.
[edit] References
$ and $-n$. == References == {{#RefList:}} [[Category:Exercises]] [[Category:Exercises with solution]]\Aa be an additive category and let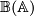 be the category of bounded chain complexes in
be the category of bounded chain complexes in 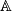 . Using the double complex extend
. Using the double complex extend  to a contravariant functor
to a contravariant functor

(ii) Suppose instead that 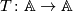 and that
and that 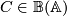 is concentrated between dimensions
is concentrated between dimensions  and
and  . Observe that the extension
. Observe that the extension 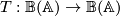 has
has 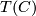 concentrated between dimensions
concentrated between dimensions  and
and 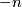 .
.