Talk:Chain duality I (Ex)
From Manifold Atlas
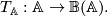
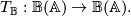
 be a chain complex in
be a chain complex in 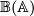 , applying
, applying 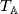 we get the double complex
we get the double complex 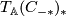 :
:
![\displaystyle \xymatrix{ & \vdots \ar[d] & \vdots \ar[d] & \vdots \ar[d] & \\ \ldots \ar[r] & T_\mathbb{A}(C_{i-1})_{j+1} \ar[d] \ar[r] & T_\mathbb{A}(C_{i-1})_{j} \ar[d]^{T_{\mathbb{A}}((d_C)_i)_j} \ar[r] & T_\mathbb{A}(C_{i-1})_{j-1} \ar[d] \ar[r] & \\ \ldots \ar[r] & T_\mathbb{A}(C_i)_{j+1} \ar[d] \ar[r]^{(d_{T_{\mathbb{A}}(C_i)})_{j+1}} & T_\mathbb{A}(C_i)_{j} \ar[d]^{T_{\mathbb{A}}((d_C)_{i+1})_j} \ar[r]^{(d_{T_{\mathbb{A}}(C_i)})_{j}} & T_\mathbb{A}(C_i)_{j-1} \ar[d] \ar[r] & \\ \ldots \ar[r] & T_\mathbb{A}(C_{i+1})_{j+1} \ar[d] \ar[r] & T_\mathbb{A}(C_{i+1})_{j} \ar[d] \ar[r] & T_\mathbb{A}(C_{i+1})_{j-1} \ar[d] \ar[r] & \\ & \vdots & \vdots & \vdots & }](/images/math/a/e/c/aec9ca6474309e9330ed13be68d17efd.png)
This can be converted into a chain complex in the usual way:
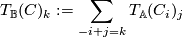
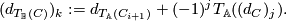
This defines what 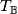 of an object is, so now we specify its behaviour on morphisms:
of an object is, so now we specify its behaviour on morphisms:
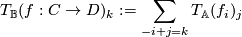
where 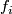 denotes the component of
denotes the component of  from
from 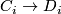 . The claim is that this defines a contravariant functor.
. The claim is that this defines a contravariant functor.
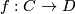 is a chain map we have
is a chain map we have 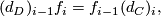
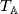 we observe that
we observe that
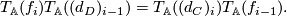
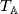 sends morphisms to morphisms,
sends morphisms to morphisms, 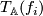 is a chain map, thus
is a chain map, thus 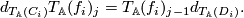
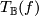 is a chain map by the commutativity of the following diagram:
is a chain map by the commutativity of the following diagram:
![\displaystyle \xymatrix{ & T_\mathbb{A}(D_i)_j \ar[dd]^{T_\mathbb{A}(f_i)_j} \ar[dl]_{d_{T_\mathbb{A}(D_i)}} \ar[dr]^{(-1)^jT_\mathbb{A}(d_{D_j})} & \\ T_\mathbb{A}(D_i)_{j-1} \ar[dd]_{T_\mathbb{A}(f_i)_{j-1}} && T_\mathbb{A}(D_{i+1})_j \ar[dd]^{T_\mathbb{A}(f_{i+1})_j} \\ & T_\mathbb{A}(C_i)_j \ar[dl]^{d_{T_\mathbb{A}(C_i)}} \ar[dr]_{(-1)^jT_\mathbb{A}(d_{C_j})} & \\ T_\mathbb{A}(C_i)_{j-1} && T_\mathbb{A}(C_{i+1})_j \\ }](/images/math/e/f/5/ef59901732884014c37ecd6e63be3d30.png)
Thus 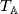 sends objects to objects and morphisms to morphisms. Functoriality of
sends objects to objects and morphisms to morphisms. Functoriality of 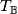 follows from that of
follows from that of 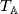 :
:
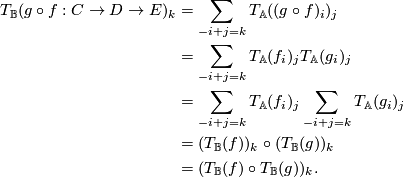
 is concentrated between dimensions
is concentrated between dimensions  and
and  and that
and that 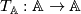 . Then looking at
. Then looking at 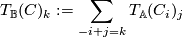
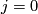 and when
and when  is between
is between  and
and  , in other words
, in other words 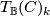 is only non-zero for
is only non-zero for  between
between 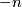 and
and  as required.
as required.