Bordism
Taras Panov (Talk | contribs) |
Taras Panov (Talk | contribs) |
||
| Line 90: | Line 90: | ||
induced from that on $W$, and $\overline{M}_2$ denotes the | induced from that on $W$, and $\overline{M}_2$ denotes the | ||
manifold with the opposite structure. The universal homotopical frameworks for geometric bordisms with additional structure | manifold with the opposite structure. The universal homotopical frameworks for geometric bordisms with additional structure | ||
| − | is provided by the theory of [[B-bordism]]s. | + | is provided by the theory of [[B-Bordism|B-bordism]]s. |
The simplest additional | The simplest additional | ||
Revision as of 12:17, 10 March 2010
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:46, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Taras Panov. No other user may edit this page at present. |
Contents |
1 Introduction
The theory of bordism is is one of the most deep and influential parts of the algebraic topology, which experienced a spectacular development in the 1960s. The main introductory reference is the monograph [Stong1968].
Basic geometric constructions of bordisms and cobordisms, as well as homotopical definitions are summarised here. For the more specific information, see B-Bordism and pages on specific bordism theories, such as unoriented, oriented and complex.
2 The bordism relation
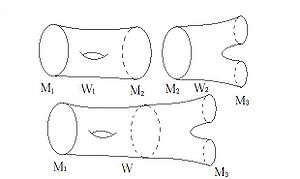
All manifolds here are assumed to be smooth, compact and closed
(without boundary), unless otherwise specified. Given two
 -dimensional manifolds
-dimensional manifolds  and
and 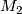 , a bordism
between them is an
, a bordism
between them is an 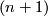 -dimensional manifold
-dimensional manifold  with boundary,
whose boundary is the disjoint union of
with boundary,
whose boundary is the disjoint union of  and
and 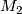 , that is,
, that is,
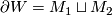 . If such
. If such  exists,
exists,  and
and 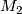 are called bordant. The bordism relation splits manifolds
into equivalence classes (see Figure), which are called
bordism classes.
are called bordant. The bordism relation splits manifolds
into equivalence classes (see Figure), which are called
bordism classes.
3 Unoriented bordism
We denote the bordism class of  by
by ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) , and denote by
, and denote by
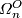 the set of bordism classes of
the set of bordism classes of  -dimensional
manifolds. Then
-dimensional
manifolds. Then 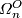 is an abelian group with respect
to the disjoint union operation:
is an abelian group with respect
to the disjoint union operation: ![[M_1]+[M_2]=[M_1\sqcup M_2]](/images/math/3/b/8/3b87653a49a8ea82afbc2c15dc9e95e6.png) .
Zero is represented by the bordism class of an empty set (which is
counted as a manifold in any dimension), or by the bordism class
of any manifold which bounds. We also have
.
Zero is represented by the bordism class of an empty set (which is
counted as a manifold in any dimension), or by the bordism class
of any manifold which bounds. We also have ![-[M]=[M]](/images/math/9/a/b/9ab407174f27a49e5094218d6baa4dbc.png) , so that
, so that
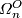 is a 2-torsion group.
is a 2-torsion group.
Set 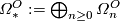 . The
product of bordism classes, namely
. The
product of bordism classes, namely ![[M_1]\times [M_2]=[M_1 \times M_2]](/images/math/b/c/a/bca399878134d24055d89500866ba471.png) , makes
, makes 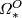 a graded commutative ring known as
the unoriented bordism ring.
a graded commutative ring known as
the unoriented bordism ring.
For any (good) space  the bordism relation can be extended to
maps of
the bordism relation can be extended to
maps of  -dimensional manifolds to
-dimensional manifolds to  : two maps
: two maps  and
and
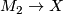 are bordant if there is a bordism
are bordant if there is a bordism  between
between
 and
and 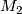 and the map
and the map 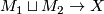 extends to a map
extends to a map
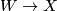 . The set of bordism classes of maps
. The set of bordism classes of maps 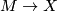 forms an
abelian group called the group of
forms an
abelian group called the group of  -dimensional unoriented
bordisms of
-dimensional unoriented
bordisms of  and denoted
and denoted 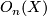 (other notations:
(other notations: 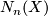 ,
,
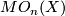 ).
).
The assignment 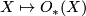 defines a generalised
homology theory, that is, satisfies the homotopy invariance, has
the excision property and exact sequences of pairs. For this
theory we have
defines a generalised
homology theory, that is, satisfies the homotopy invariance, has
the excision property and exact sequences of pairs. For this
theory we have 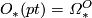 , and
, and 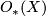 is an
is an
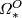 -module.
-module.
The Pontrjagin--Thom construction reduces the calculation of the bordism groups to a homotopical problem:
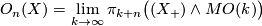
where 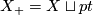 , and
, and 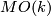 is the Thom space of
the universal vector
is the Thom space of
the universal vector  -plane bundle
-plane bundle 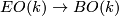 . The
cobordism groups are defined dually:
. The
cobordism groups are defined dually:
![\displaystyle O^n(X)=\lim_{k\to\infty}[\Sigma^{k-n}(X_+),MO(k)]](/images/math/b/b/0/bb05a687d97e200b92528c433a6d0273.png)
where ![[X,Y]](/images/math/e/1/9/e1921829b3d333bdf8227e9d46cb530b.png) denotes the set of homotopy classes of maps from
denotes the set of homotopy classes of maps from  to
to  . The resulting generalised cohomology theory is
multiplicative, which implies that
. The resulting generalised cohomology theory is
multiplicative, which implies that 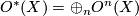 is a
graded commutative ring. It follows from the definitions that
is a
graded commutative ring. It follows from the definitions that
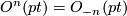 . The graded ring
. The graded ring 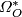 with
with
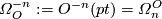 is called the
unoriented cobordism ring. It has nonzero elements only in
nonpositively graded components. The bordism ring
is called the
unoriented cobordism ring. It has nonzero elements only in
nonpositively graded components. The bordism ring 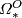 and the cobordism ring
and the cobordism ring 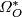 differ only by their
gradings, so the notions of the "bordism class" and "cobordism
class" of a manifold
differ only by their
gradings, so the notions of the "bordism class" and "cobordism
class" of a manifold  are interchangeable. The difference
between bordism and cobordism appears only for nontrivial
spaces
are interchangeable. The difference
between bordism and cobordism appears only for nontrivial
spaces  .
.
4 Oriented and complex
The most important examples of bordism theories arise from
extending the bordism relation to manifolds endowed with some
additional structure. To take account of this structure in the
definition of bordism one requires that 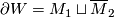 , where the structure on
, where the structure on 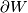 is
induced from that on
is
induced from that on  , and
, and 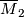 denotes the
manifold with the opposite structure. The universal homotopical frameworks for geometric bordisms with additional structure
is provided by the theory of B-bordisms.
denotes the
manifold with the opposite structure. The universal homotopical frameworks for geometric bordisms with additional structure
is provided by the theory of B-bordisms.
The simplest additional
structure is an orientation. The \emph{oriented bordism} relation
arises accordingly. The \emph{oriented bordism ring}
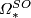 is defined similarly to
is defined similarly to 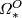 , with
the only difference that
, with
the only difference that ![-[M]=[\overline{M}]](/images/math/5/b/5/5b55530daf53ecbd204d322a03982b78.png) . Elements of
. Elements of
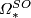 generally do not have order~2.
generally do not have order~2.
Complex structure gives another important example of an additional
structure on manifolds. However, a direct attempt to define the
bordism relation on complex manifolds fails because the manifold
 is odd-dimensional and therefore cannot be complex. This can
be remedied by considering \emph{stably complex} (also known as
\emph{stably almost complex} or \emph{quasicomplex}) structures.
is odd-dimensional and therefore cannot be complex. This can
be remedied by considering \emph{stably complex} (also known as
\emph{stably almost complex} or \emph{quasicomplex}) structures.
Let 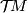 denote the tangent bundle of~
denote the tangent bundle of~ , and
, and
Tex syntax errorthe product vector bundle
Tex syntax error
over~ . A \emph{tangential stably complex structure} on
. A \emph{tangential stably complex structure} on  is
determined by a choice of an isomorphism
is
determined by a choice of an isomorphism
Tex syntax error
between the ``stable tangent bundle and a complex vector
bundle~ over~
over~ . Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in~[ston68, Ch.~II,~VII]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A \emph{normal stably complex
structure} on
. Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in~[ston68, Ch.~II,~VII]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A \emph{normal stably complex
structure} on  is determined by a choice of a complex bundle
structure in the normal bundle
is determined by a choice of a complex bundle
structure in the normal bundle 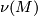 of an embedding
of an embedding
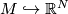 . A tangential and normal stably
complex structures on
. A tangential and normal stably
complex structures on  determine each other by means of the
determine each other by means of the
Tex syntax error. We therefore may restrict
our attention to tangential structures only.
By a \emph{stably complex manifold} we mean a pair 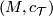 consisting of a manifold
consisting of a manifold  and a stably complex structure
and a stably complex structure
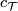 on it. This is a generalisation to a complex and
\emph{almost complex} manifold (where the latter means a manifold
with a choice of a complex structure on
on it. This is a generalisation to a complex and
\emph{almost complex} manifold (where the latter means a manifold
with a choice of a complex structure on 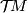 , i.e. a
stably complex structure~\eqref{scs} with
, i.e. a
stably complex structure~\eqref{scs} with  ).
%The following
%example shows that a manifold may admit many different stably
%complex structures.
).
%The following
%example shows that a manifold may admit many different stably
%complex structures.
\begin{example}
Let 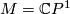 . The standard complex structure on
. The standard complex structure on  is
equivalent to a stably complex structure determined by the
isomorphism
\[
is
equivalent to a stably complex structure determined by the
isomorphism
\[
{\mathcal T}(\mathbb{C}P^1)\oplus\underline{\R}^2\stackrel{\cong}{\longrightarrow}
\overline{\eta}\oplus \overline{\eta}
\]
where 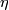 is the Hopf line bundle. On the other hand, the
isomorphism
\[
is the Hopf line bundle. On the other hand, the
isomorphism
\[
{\mathcal T}(\mathbb{C}P^1)\oplus\underline{\R}^2\stackrel{\cong}{\longrightarrow}
\eta\oplus \overline{\eta}\cong \underline{\C}^2
\]
determines a trivial stably complex structure on~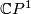 .
\end{example}
.
\end{example}
The bordism relation can be defined between stably complex
manifolds. Like the case of unoriented bordisms, the set of
bordism classes ![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) of stably complex manifolds
is an Abelian group with respect to the disjoint union. This group
is called the \emph{group of
of stably complex manifolds
is an Abelian group with respect to the disjoint union. This group
is called the \emph{group of  -dimensional complex bordisms} and
denoted
-dimensional complex bordisms} and
denoted 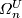 . A zero is represented by the bordism
class of any manifold
. A zero is represented by the bordism
class of any manifold  which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
Tex syntax error). The sphere
 provides an example
provides an example
of such manifold. The opposite element to the bordism class
![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) in the group
in the group 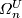 may be
represented by the same manifold
may be
represented by the same manifold  with the stably complex
structure determined by the isomorphism
\[
with the stably complex
structure determined by the isomorphism
\[
{\mathcal T}\!M\oplus\underline{\R}^k\oplus\underline{\R}^2\stackrel{c_{\mathcal T}\oplus
e}{\lllra}\xi\oplus\underline{\C}
\]
where 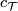 is given as in~\eqref{scs}, and
is given as in~\eqref{scs}, and
Tex syntax error,
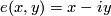 .
.
We shall use the abbreviated notation ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) for the complex
bordism class whenever the stably complex structure
for the complex
bordism class whenever the stably complex structure 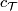 is clear from the context.
is clear from the context.
5 References
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
- [ston68] Template:Ston68
|
This page has not been refereed. The information given here might be incomplete or provisional. |