Bordism
Taras Panov (Talk | contribs) |
m (→External links) |
||
| (120 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
== Introduction == | == Introduction == | ||
| − | The theory of bordism | + | The theory of bordism is one of the deepest and most influential parts of |
| − | + | algebraic topology. The foundations of bordism were laid in the pioneering works of Pontrjagin \cite{Pontryagin1959} and Thom \cite{Thom1954}, and the theory experienced a spectacular development in the 1960s. In particular, Atiyah \cite{Atiyah1961} showed that bordism is a [[Wikipedia:homology theory|generalised homology theory]] and related it to the emergent [[Wikipedia:K-theory|<i>K</i>-theory]]. The main introductory reference is the monograph \cite{Stong1968}. | |
| − | Basic geometric constructions of | + | Basic geometric constructions of bordism and cobordism, as well as homotopical definitions are summarised here. For more information, see the pages in the category '''[[:Category:Bordism|Bordism]]'''. |
| + | <!-- | ||
| + | * [[Unoriented bordism|Unoriented bordism]] | ||
| + | * [[Oriented bordism|Oriented bordism]] | ||
| + | * [[Spin bordism|Spin bordism]] | ||
| + | * [[Complex bordism|Complex bordism]] | ||
| + | * [[B-Bordism|B-bordism]].--> | ||
== The bordism relation == | == The bordism relation == | ||
| − | |||
<wikitex>; | <wikitex>; | ||
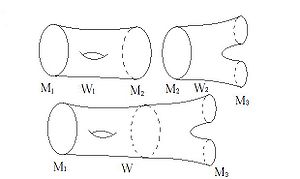
All manifolds here are assumed to be smooth, compact and closed | All manifolds here are assumed to be smooth, compact and closed | ||
(without boundary), unless otherwise specified. Given two | (without boundary), unless otherwise specified. Given two | ||
$n$-dimensional manifolds $M_1$ and $M_2$, a ''bordism'' | $n$-dimensional manifolds $M_1$ and $M_2$, a ''bordism'' | ||
| − | between them is an $(n+1)$-dimensional manifold $W$ with boundary, | + | between them is an $(n+1)$-dimensional manifold $\,W$ with boundary, |
whose boundary is the disjoint union of $M_1$ and $M_2$, that is, | whose boundary is the disjoint union of $M_1$ and $M_2$, that is, | ||
| − | $\partial W=M_1\sqcup M_2$. If such $W$ exists, $M_1$ and $M_2$ | + | $\partial W=M_1\sqcup M_2$. If such a $\,W$ exists, $M_1$ and $M_2$ |
are called ''bordant''. The bordism relation splits manifolds | are called ''bordant''. The bordism relation splits manifolds | ||
| − | into equivalence classes (see Figure), which are called | + | into equivalence classes (see the Figure), which are called |
''bordism classes''. | ''bordism classes''. | ||
[[Image:trcob.jpg|thumb|300px|Transitivity of the bordism relation]] | [[Image:trcob.jpg|thumb|300px|Transitivity of the bordism relation]] | ||
</wikitex> | </wikitex> | ||
| − | |||
== Unoriented bordism == | == Unoriented bordism == | ||
| Line 31: | Line 33: | ||
Zero is represented by the bordism class of an empty set (which is | Zero is represented by the bordism class of an empty set (which is | ||
counted as a manifold in any dimension), or by the bordism class | counted as a manifold in any dimension), or by the bordism class | ||
| − | of any manifold which bounds. We also have $ | + | of any manifold which bounds. We also have $\partial(M\times I)=M\sqcup M$. |
| − | $\varOmega_n^O$ is a 2-torsion group. | + | Hence, $2[M]=0$ and $\varOmega_n^O$ is a 2-torsion group. |
Set $\varOmega _*^O:=\bigoplus _{n \ge 0}\varOmega _n^O$. The | Set $\varOmega _*^O:=\bigoplus _{n \ge 0}\varOmega _n^O$. The | ||
| Line 39: | Line 41: | ||
the ''unoriented bordism ring''. | the ''unoriented bordism ring''. | ||
| − | For any | + | For any space $X$ the bordism relation can be extended to |
maps of $n$-dimensional manifolds to $X$: two maps $M_1\to X$ and | maps of $n$-dimensional manifolds to $X$: two maps $M_1\to X$ and | ||
| − | $M_2\to X$ are ''bordant'' if there is a bordism $W$ between | + | $M_2\to X$ are ''bordant'' if there is a bordism $\,W$ between |
$M_1$ and $M_2$ and the map $M_1\sqcup M_2\to X$ extends to a map | $M_1$ and $M_2$ and the map $M_1\sqcup M_2\to X$ extends to a map | ||
$W\to X$. The set of bordism classes of maps $M\to X$ forms an | $W\to X$. The set of bordism classes of maps $M\to X$ forms an | ||
| − | abelian group called the '' | + | abelian group called the ''$n$-dimensional unoriented bordism group of $X$'' and denoted $O_n(X)$ (other notations: $\mathfrak N_n(X)$, $MO_n(X)$). |
| − | + | ||
| − | $MO_n(X)$). | + | |
| − | The assignment $X\mapsto O_*(X)$ defines a [[ | + | The assignment $X\mapsto O_*(X)$ defines a |
| − | homology theory]], that is, | + | [[Wikipedia:Homology_theory|generalised homology theory]], that is, it is functorial in $X$, homotopy |
| − | the excision property and exact sequences of pairs. For this | + | invariant, has the excision property and exact sequences of pairs. For this |
theory we have $O_*(pt)=\varOmega_*^O$, and $O_*(X)$ is an | theory we have $O_*(pt)=\varOmega_*^O$, and $O_*(X)$ is an | ||
$\varOmega_*^O$-module. | $\varOmega_*^O$-module. | ||
| − | The | + | The [[B-Bordism#The Pontrjagin-Thom isomorphism|Pontrjagin-Thom construction]] reduces the calculation |
of the bordism groups to a homotopical problem: | of the bordism groups to a homotopical problem: | ||
$$ | $$ | ||
O_n(X)=\lim_{k\to\infty}\pi_{k+n}\bigl((X_+)\wedge MO(k)\bigr) | O_n(X)=\lim_{k\to\infty}\pi_{k+n}\bigl((X_+)\wedge MO(k)\bigr) | ||
$$ | $$ | ||
| − | where $X_+=X\sqcup pt$, and $MO(k)$ is the | + | where $X_+=X\sqcup pt$, and $MO(k)$ is the [[Wikipedia:Thom_space|Thom space]] of |
the universal vector $k$-plane bundle $EO(k)\to BO(k)$. The | the universal vector $k$-plane bundle $EO(k)\to BO(k)$. The | ||
''cobordism groups'' are defined dually: | ''cobordism groups'' are defined dually: | ||
| Line 65: | Line 65: | ||
O^n(X)=\lim_{k\to\infty}[\Sigma^{k-n}(X_+),MO(k)] | O^n(X)=\lim_{k\to\infty}[\Sigma^{k-n}(X_+),MO(k)] | ||
$$ | $$ | ||
| − | where $[X,Y]$ denotes the set of homotopy classes of maps from $X$ | + | where $[X,Y]$ denotes the set of based homotopy classes of maps from $X$ to $Y$. The resulting generalised cohomology theory is multiplicative, which implies that $O^*(X)=\bigoplus_n O^n(X)$ is a graded commutative ring. It follows from the definitions that $O^n(pt)=O_{-n}(pt)$. The graded ring $\varOmega^*_O$ with $\varOmega^{-n}_O:=O^{-n}(pt)=\varOmega_n^O$ is called the ''unoriented cobordism ring''. It has nonzero elements only in nonpositively graded components. The bordism ring $\varOmega^O_*$ and the cobordism ring $\varOmega_O^*$ differ only by their gradings, so the notions of the "bordism class" and "cobordism class" of a manifold $M$ are interchangeable. The difference between bordism and cobordism appears only when one considers generalised homology and cohomology theories. |
| − | to $Y$. The resulting generalised cohomology theory is | + | |
| − | multiplicative, which implies that $O^*(X)=\ | + | |
| − | graded commutative ring. It follows from the definitions that | + | |
| − | $O^n(pt)=O_{-n}(pt)$. The graded ring $\varOmega^*_O$ with | + | |
| − | $\varOmega^{-n}_O:=O^{-n}(pt)=\varOmega_n^O$ is called the | + | |
| − | ''unoriented cobordism ring''. It has nonzero elements only in | + | |
| − | nonpositively graded components. The bordism ring $\varOmega^O_*$ | + | |
| − | and the cobordism ring $\varOmega_O^*$ differ only by their | + | |
| − | gradings, so the notions of the "bordism class" and "cobordism | + | |
| − | class" of a manifold $M$ are interchangeable. The difference | + | |
| − | between bordism and cobordism appears only | + | |
| − | + | ||
</wikitex> | </wikitex> | ||
| − | |||
== Oriented and complex bordism == | == Oriented and complex bordism == | ||
<wikitex>; | <wikitex>; | ||
| − | The | + | The bordism relation may be extended to manifolds endowed with some |
| − | + | additional structure, which leads to the most important examples of | |
| − | additional structure | + | bordism theories. The universal homotopical framework for geometric bordism with additional structure is provided by the theory of [[B-Bordism|B-bordism]]. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | is provided by the theory of [[B-Bordism|B-bordism]] | + | |
| − | The simplest additional | + | <!-- |
| − | structure is an orientation. | + | To take account of this structure in the definition of bordism one requires that $\partial W=M_1\sqcup\overline{M}_2$, where the structure on $\,\partial W$ is induced from that on $\,W$, and $\overline{M}$ denotes the manifold with the opposite structure. |
| − | + | --> | |
| − | $\ | + | The simplest additional structure is an orientation. By definition, two oriented $n$-dimensional manifolds $M_1$ and $M_2$ are ''oriented bordant'' if there is an oriented $(n+1)$-dimensional manifold $W$ with boundary such that $\partial |
| − | the | + | W=M_1\sqcup\overline{M}_2$, where $\overline M_2$ denotes $M_2$ with the orientation reversed. The ''oriented bordism groups'' |
| + | $\varOmega_n^{SO}$ and the ''oriented bordism ring'' $\varOmega_*^{SO}=\bigoplus_{n\ge0}\varOmega_n^{SO}$ are defined | ||
| + | accordingly. Given an oriented manifold $M$, the manifold ${}M\times I$ has a canonical orientation such that $\partial(M\times | ||
| + | I)=M\sqcup\overline M$. Hence, $-[M]=[\overline{M}]$ in $\varOmega_n^{SO}$. Unlike $\varOmega_n^O$, elements of | ||
$\varOmega_*^{SO}$ generally do not have order 2. | $\varOmega_*^{SO}$ generally do not have order 2. | ||
| Line 102: | Line 87: | ||
structure on manifolds. However, a direct attempt to define the | structure on manifolds. However, a direct attempt to define the | ||
bordism relation on complex manifolds fails because the manifold | bordism relation on complex manifolds fails because the manifold | ||
| − | $W$ is odd-dimensional and therefore cannot be complex. This can | + | $\,W$ is odd-dimensional and therefore cannot be complex. This can |
be remedied by considering ''stably complex'' (also known as | be remedied by considering ''stably complex'' (also known as | ||
''weakly almost complex'', ''stably almost complex'' or ''quasicomplex'') structures. | ''weakly almost complex'', ''stably almost complex'' or ''quasicomplex'') structures. | ||
| Line 111: | Line 96: | ||
$$ | $$ | ||
c_{\mathcal T}\colon {\mathcal T}\!M\oplus \underline{\mathbb R}^k\to \xi | c_{\mathcal T}\colon {\mathcal T}\!M\oplus \underline{\mathbb R}^k\to \xi | ||
| − | |||
$$ | $$ | ||
between the "stable" tangent bundle and a complex vector | between the "stable" tangent bundle and a complex vector | ||
bundle $\xi$ over $M$. Some of the choices of such isomorphisms | bundle $\xi$ over $M$. Some of the choices of such isomorphisms | ||
| − | are deemed to be equivalent, i.e. | + | are deemed to be equivalent, i.e. determine the same stably |
complex structures (see details in Chapters II and VII of \cite{Stong1968}). In | complex structures (see details in Chapters II and VII of \cite{Stong1968}). In | ||
particular, two stably complex structures are equivalent if they | particular, two stably complex structures are equivalent if they | ||
| − | differ by a trivial complex summand. A ''normal stably complex | + | differ by a trivial complex summand. A ''normal stably complex structure'' on $M$ is determined by a choice of a complex bundle |
| − | structure'' on $M$ is determined by a choice of a complex bundle | + | structure on the normal bundle $\nu(M)$ of an embedding |
| − | structure | + | $M\hookrightarrow\mathbb R^N$. Tangential and normal stably |
| − | $M\hookrightarrow\mathbb R^N$. | + | |
complex structures on $M$ determine each other by means of the | complex structures on $M$ determine each other by means of the | ||
canonical isomorphism $\mathcal | canonical isomorphism $\mathcal | ||
| Line 129: | Line 112: | ||
A ''stably complex manifold'' is a pair $(M,c_{\mathcal | A ''stably complex manifold'' is a pair $(M,c_{\mathcal | ||
T})$ consisting of a manifold $M$ and a stably complex structure | T})$ consisting of a manifold $M$ and a stably complex structure | ||
| − | $c_{\mathcal T}$ on it. This is a generalisation | + | $c_{\mathcal T}$ on it. This is a generalisation of a complex and |
''almost complex'' manifold (where the latter means a manifold | ''almost complex'' manifold (where the latter means a manifold | ||
with a choice of a complex structure on ${\mathcal T}\!M$, i.e. a | with a choice of a complex structure on ${\mathcal T}\!M$, i.e. a | ||
| − | stably complex structure with $k=0$) | + | stably complex structure $c_{\mathcal T}$ with $k=0$). |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {{beginrem|Example}} | |
Let $M=\mathbb{C}P^1$. The standard complex structure on $M$ is | Let $M=\mathbb{C}P^1$. The standard complex structure on $M$ is | ||
| − | equivalent to | + | equivalent to the stably complex structure determined by the |
isomorphism | isomorphism | ||
| − | + | $$ | |
| − | {\mathcal T}(\mathbb{C}P^1)\oplus\underline{\R}^2\stackrel{\cong}{\longrightarrow} | + | {\mathcal T}(\mathbb{C}P^1)\oplus\underline{\mathbb R}^2\stackrel{\cong}{\longrightarrow} |
\overline{\eta}\oplus \overline{\eta} | \overline{\eta}\oplus \overline{\eta} | ||
| − | + | $$ | |
where $\eta$ is the Hopf line bundle. On the other hand, the | where $\eta$ is the Hopf line bundle. On the other hand, the | ||
isomorphism | isomorphism | ||
| − | + | $$ | |
| − | {\mathcal T}(\mathbb{C}P^1)\oplus\underline{\R}^2\stackrel{\cong}{\longrightarrow} | + | {\mathcal T}(\mathbb{C}P^1)\oplus\underline{\mathbb R}^2\stackrel{\cong}{\longrightarrow} |
| − | \eta\oplus \overline{\eta}\cong \underline{\C}^2 | + | \eta\oplus \overline{\eta}\cong \underline{\mathbb C}^2 |
| − | + | $$ | |
| − | determines a trivial stably complex structure on | + | determines a trivial stably complex structure on $\mathbb C P^1$. |
| − | + | {{endrem}} | |
The bordism relation can be defined between stably complex | The bordism relation can be defined between stably complex | ||
| − | manifolds. Like the case of unoriented | + | manifolds. Like the case of unoriented bordism, the set of |
| − | bordism classes $[M,c_{\mathcal T}]$ of stably complex manifolds | + | bordism classes $[M,c_{\mathcal T}]$ of $n$-dimensional stably complex manifolds is an Abelian group with respect to the disjoint union. This group is called the ''$n$-dimensional complex bordism group'' and |
| − | is an Abelian group with respect to the disjoint union. This group | + | denoted by $\varOmega^U_n$. The zero is represented by the bordism |
| − | is called the | + | |
| − | denoted $\varOmega^U_n$. | + | |
class of any manifold $M$ which bounds and whose stable tangent | class of any manifold $M$ which bounds and whose stable tangent | ||
bundle is trivial (and therefore isomorphic to a product complex | bundle is trivial (and therefore isomorphic to a product complex | ||
| − | vector bundle $M\times\C^k$). The sphere $S^n$ provides an example | + | vector bundle $M\times\mathbb C^k$). The sphere $S^n$ provides an example |
| − | of such manifold. The opposite element to the bordism class | + | of such a manifold. The opposite element to the bordism class |
$[M,c_{\mathcal T}]$ in the group $\varOmega^U_n$ may be | $[M,c_{\mathcal T}]$ in the group $\varOmega^U_n$ may be | ||
represented by the same manifold $M$ with the stably complex | represented by the same manifold $M$ with the stably complex | ||
structure determined by the isomorphism | structure determined by the isomorphism | ||
| − | + | $$ | |
| − | {\mathcal T}\!M\oplus\underline{\R}^k\oplus\underline{\R}^2\stackrel{c_{\mathcal T}\oplus | + | {\mathcal T}\!M\oplus\underline{\mathbb R}^k\oplus\underline{\mathbb R}^2\stackrel{c_{\mathcal T}\oplus |
| − | e}{\ | + | e}{-\hspace{-5pt}-\hspace{-5pt}\longrightarrow}\xi\oplus\underline{\mathbb C} |
| − | + | $$ | |
| − | + | where $e\colon\mathbb R^2\to\mathbb C$ is given by $e(x,y)=x-iy$. | |
| − | $e\colon\R^2\to\C$ | + | |
| − | + | An abbreviated notation $[M]$ for the complex | |
| − | bordism class whenever the stably complex structure $c_{\mathcal | + | bordism class will be used whenever the stably complex structure $c_{\mathcal |
T}$ is clear from the context. | T}$ is clear from the context. | ||
| + | |||
| + | The ''complex bordism and cobordism groups'' of a space | ||
| + | $X$ are defined similarly to the [[#Unoriented bordism|unoriented]] case: | ||
| + | $$ | ||
| + | \begin{aligned} | ||
| + | U_n(X)&=\lim_{k\to\infty}\pi_{2k+n}((X_+)\wedge MU(k)),\\ | ||
| + | U^n(X)&=\lim_{k\to\infty}[\Sigma^{2k-n}(X_+),MU(k)] | ||
| + | \end{aligned} | ||
| + | $$ | ||
| + | where $MU(k)$ is the Thom space of the universal complex $k$-plane | ||
| + | bundle $EU(k)\to BU(k)$. These groups are $\varOmega_*^U$-modules | ||
| + | and give rise to a multiplicative [[Wikipedia:Homology_theory|(co)homology theory]]. In | ||
| + | particular, $U^*(X)=\bigoplus_n U^n(X)$ is a graded ring. | ||
| + | |||
| + | The graded ring $\varOmega^*_U$ with $\varOmega^{n}_U=\varOmega_{-n}^U$ is | ||
| + | called the ''complex cobordism ring''; it has nontrivial | ||
| + | elements only in nonpositively graded components. | ||
</wikitex> | </wikitex> | ||
| + | == Connected sum and bordism == | ||
| + | <wikitex>; | ||
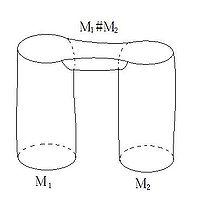
| + | For manifolds of positive dimension the disjoint union $M_1\sqcup M_2$ representing the sum of bordism classes $[M_1]+[M_2]$ may be | ||
| + | replaced by their "[[Parametric connected sum#Connected sum|connected sum]]", which represents the same | ||
| + | bordism class. | ||
| − | + | The connected sum $M_1\mathbin\# M_2$ of manifolds $M_1$ and $M_2$ of the same dimension $n$ is constructed as follows. Choose points $v_1\in M_1$ and $v_2\in M_2$, and take closed $\varepsilon$-balls | |
| − | + | $B_\varepsilon(v_1)$ and $B_\varepsilon(v_2)$ around them (both | |
| + | manifolds may be assumed to be endowed with a Riemannian metric). | ||
| + | Fix an isometric embedding $f$ of a pair of standard | ||
| + | $\varepsilon$-balls $D^n\times S^0$ (here $S^0=\{0,1\}$) into | ||
| + | $M_1\sqcup M_2$ which maps $D^n\times0$ onto $B_\varepsilon(v_1)$ | ||
| + | and $D^n\times1$ onto $B_\varepsilon(v_2)$. If both $M_1$ and $M_2$ are oriented | ||
| + | we additionally require the embedding $f$ to preserve the | ||
| + | orientation on the first ball and reverse in on the second. Now, using this | ||
| + | embedding, replace in $M_1\sqcup M_2$ the pair of balls $D^n\times | ||
| + | S^0$ by a "pipe" $S^{n-1}\times D^1$. After smoothing the | ||
| + | angles in the standard way we obtain a smooth manifold $M_1\mathbin\# M_2$. | ||
| − | + | If both $M_1$ and $M_2$ are connected the smooth structure on $M_1\mathbin\# M_2$ does not depend on a choice | |
| − | + | of points $v_1$, $v_2$ and embedding $D^n\times | |
| + | S^0\hookrightarrow M_1\sqcup M_2$. It does however depend on the orientations; $M_1\mathbin\# M_2$ and $M_1\mathbin\#\overline{M_2}$ | ||
| + | are not diffeomorphic in general. | ||
| − | + | There are smooth contraction maps $p_1\colon M_1\mathbin\# M_2\to M_1$ and | |
| + | $p_2\colon M_1\mathbin\# M_2\to M_2$. In the oriented case the manifold | ||
| + | $M_1\mathbin\# M_2$ can be oriented in such a way that both contraction | ||
| + | maps preserve the orientations. | ||
| − | + | [[Image:figcs.jpg|thumb|200px|Disjoint union and connected sum]] | |
| + | |||
| + | A bordism between $M_1\sqcup M_2$ and $M_1\mathbin\# M_2$ may be | ||
| + | constructed as follows. Consider a cylinder $M_1\times I$, from | ||
| + | which we remove an $\varepsilon$-neighbourhood | ||
| + | $U_\varepsilon(v_1\times1)$ of the point $v_1\times 1$. Similarly, | ||
| + | remove the neighbourhood $U_\varepsilon(v_2\times1)$ from | ||
| + | $M_2\times I$ (each of these two neighbourhoods can be identified | ||
| + | with the half of a standard open $(n+1)$-ball). Now connect the | ||
| + | two remainders of cylinders by a "half pipe" $S^n_\le\times I$ in | ||
| + | such a way that the half-sphere $S^n_\le\times 0$ is identified | ||
| + | with the half-sphere on the boundary of | ||
| + | $U_\varepsilon(v_1\times1)$, and $S^n_\le\times1$ is identified | ||
| + | with the half-sphere on the boundary of $U_\varepsilon(v_2\times | ||
| + | 1)$. Smoothening the angles we obtain a manifold with boundary | ||
| + | $M_1\sqcup M_2\sqcup(M_1\mathbin\# M_2)$ (or | ||
| + | $\overline{M_1}\sqcup\overline{M_2}\sqcup(M_1\mathbin\# M_2)$ in the | ||
| + | oriented case), see the Figure. | ||
| + | |||
| + | If $M_1$ and $M_2$ are stably complex manifolds, then | ||
| + | there is a canonical stably complex structure on $M_1\mathbin\# M_2$, | ||
| + | which is constructed as follows. Assume the stably complex | ||
| + | structures on $M_1$ and $M_2$ are determined by isomorphisms | ||
| + | $$ | ||
| + | c_{\mathcal T\!,1}\colon{\mathcal T}\!M_1\oplus\underline{\mathbb R}^{k_1}\to\xi_1 | ||
| + | \quad\text{and}\quad | ||
| + | c_{\mathcal T\!,2}\colon{\mathcal T}\!M_2\oplus\underline{\mathbb R}^{k_2}\to\xi_2. | ||
| + | $$ | ||
| + | Using the isomorphism ${\mathcal T}(M_1\mathbin\# | ||
| + | M_2)\oplus\underline{\mathbb R}^n\cong p_1^*{\mathcal T}\!M_1\oplus | ||
| + | p_2^*{\mathcal T}\!M_2$, we define a stably complex structure on | ||
| + | $M_1\mathbin\# M_2$ by the isomorphism | ||
| + | $$ | ||
| + | {\mathcal T}(M_1\mathbin\# M_2)\oplus\underline{\mathbb R}^{n+k_1+k_2} | ||
| + | \cong | ||
| + | p_1^*{\mathcal T}\!M_1\oplus\underline{\mathbb R}^{k_1}\oplus | ||
| + | p_2^*{\mathcal T}\!M_2\oplus\underline{\mathbb R}^{k_2} | ||
| + | \xrightarrow{c_{{\mathcal T},1}\oplus c_{{\mathcal T},2}} | ||
| + | p_1^*\xi_1\oplus p_2^*\xi_2. | ||
| + | $$ | ||
| + | This stably complex structure is called the | ||
| + | ''connected sum of stably complex structures'' on $M_1$ and | ||
| + | $M_2$. The corresponding complex bordism class is $[M_1]+[M_2]$. | ||
| + | </wikitex> | ||
| + | |||
| + | == Structure results == | ||
| + | <wikitex>; | ||
| + | The theory of unoriented (co)bordism was first to be completed: its coefficient ring $\varOmega_*^O$ was calculated by Thom, and the bordism groups $O_*(X)$ of cell complexes $X$ were reduced to | ||
| + | homology groups of $X$ with coefficients in $\varOmega_*^O$. The | ||
| + | corresponding results are summarised as follows: | ||
| + | |||
| + | {{beginthm|Theorem}} | ||
| + | #Two manifolds are unorientedly bordant if and only if they have identical sets of Stiefel-Whitney characteristic numbers. | ||
| + | #$\varOmega_*^O$ is a polynomial ring over $\mathbb Z/2$ with one generator $a_i$ in every positive dimension $i\ne 2^k-1$. | ||
| + | #For every cell complex $X$ the module $O_*(X)$ is a free graded $\varOmega_*^O$-module isomorphic to $H_*(X;\mathbb Z/2)\otimes_{\mathbb Z/2}\varOmega_*^O$. | ||
| + | {{endthm}} | ||
| + | |||
| + | Parts 1 and 2 were proved in \cite{Thom1954}. Part 3 was proved in \cite{Conner&Floyd1964}. | ||
| + | |||
| + | Calculating the complex bordism ring $\varOmega_*^U$ turned out to | ||
| + | be a much more difficult problem: | ||
| + | |||
| + | {{beginthm|Theorem}} | ||
| + | #$\varOmega_*^U\otimes\mathbb Q$ is a polynomial ring over $\mathbb Q$ generated by the bordism classes of complex projective spaces $\mathbb C P^i$, $i\ge1$. | ||
| + | #Two stably complex manifolds are bordant if and only if they have identical sets of Chern characteristic numbers. | ||
| + | #$\varOmega_*^U$ is a polynomial ring over $\mathbb Z$ with one generator $a_i$ in every even dimension $2i$, where $i\ge1$. | ||
| + | {{endthm}} | ||
| + | |||
| + | Part 1 can be proved by the methods of Thom. Part 2 follows from | ||
| + | the results of \cite{Milnor1960} and \cite{Novikov1960}. Part 3 is the most difficult one; it was done in 1960 in \cite{Novikov1960} (see also \cite{Novikov1962} for a more detailed | ||
| + | account) and Milnor (unpublished, but see \cite{Thom1995}). | ||
| + | |||
| + | Note that part 3 of Theorem 6.1 does not extend to | ||
| + | complex bordism; $U_*(X)$ is not a free $\varOmega_*^U$-module in | ||
| + | general. Unlike the case of unoriented bordism, the calculation of complex bordism of a space $X$ does not reduce to | ||
| + | calculating the coefficient ring $\varOmega^U_*$ and homology | ||
| + | groups $H_*(X)$. | ||
| + | |||
| + | The calculation of the oriented bordism ring was completed by | ||
| + | \cite{Novikov1960} (ring structure modulo torsion) and \cite{Wall1960} (additive torsion), with important contributions made by | ||
| + | Rokhlin, Averbuch, and Milnor. Unlike complex bordism, the | ||
| + | ring $\varOmega_*^{SO}$ has additive torsion. We give only a partial | ||
| + | result here, which does not fully describe the torsion elements. For the complete description of the ring $\varOmega_*^{SO}$ see the [[Oriented bordism#Classification|Oriented bordism]] page. | ||
| + | |||
| + | {{beginthm|Theorem}} | ||
| + | #$\varOmega_*^{SO}\otimes\mathbb Q$ is a polynomial ring over $\mathbb Q$ generated by the bordism classes of complex projective spaces $\mathbb C P^{2i}$, $i\ge1$. | ||
| + | #The subring $\mathrm{Tors}\subset\varOmega_*^{SO}$ of torsion elements contains only elements of order 2. The quotient $\varOmega_*^{SO}/\mathrm{Tors}$ is a polynomial ring over $\mathbb Z$ with one generator $a_i$ in every dimension $4i,$ where $i\ge1$. | ||
| + | #Two oriented manifolds are bordant if and only if they have identical sets of Pontrjagin and Stiefel-Whitney characteristic numbers. | ||
| + | {{endthm}} | ||
| + | |||
| + | For more specific information about the three bordism theories, including constructions of manifolds representing polynomial generators in the bordism rings and applications, see the [[Unoriented bordism|Unoriented bordism]], [[Oriented bordism|Oriented bordism]], and [[Complex bordism|Complex bordism]] pages. | ||
| + | </wikitex> | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| − | + | == External links == | |
| + | * The Encyclopedia of Mathematics article on [http://www.encyclopediaofmath.org/index.php/Bordism bordism]. | ||
| + | * The Wikipedia page on [[Wikipedia:Cobordism|cobordism]]. | ||
[[Category:Theory]] | [[Category:Theory]] | ||
| − | + | [[Category:Bordism]] | |
| + | <!-- --> | ||
Latest revision as of 21:52, 28 March 2013
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:46, 1 April 2011 and the changes since publication. |
Contents |
[edit] 1 Introduction
The theory of bordism is one of the deepest and most influential parts of algebraic topology. The foundations of bordism were laid in the pioneering works of Pontrjagin [Pontryagin1959] and Thom [Thom1954], and the theory experienced a spectacular development in the 1960s. In particular, Atiyah [Atiyah1961] showed that bordism is a generalised homology theory and related it to the emergent K-theory. The main introductory reference is the monograph [Stong1968].
Basic geometric constructions of bordism and cobordism, as well as homotopical definitions are summarised here. For more information, see the pages in the category Bordism.
[edit] 2 The bordism relation
All manifolds here are assumed to be smooth, compact and closed
(without boundary), unless otherwise specified. Given two
 -dimensional manifolds
-dimensional manifolds  and
and 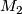 , a bordism
between them is an
, a bordism
between them is an 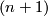 -dimensional manifold
-dimensional manifold 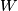 with boundary,
whose boundary is the disjoint union of
with boundary,
whose boundary is the disjoint union of  and
and 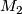 , that is,
, that is,
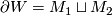 . If such a
. If such a 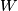 exists,
exists,  and
and 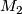 are called bordant. The bordism relation splits manifolds
into equivalence classes (see the Figure), which are called
bordism classes.
are called bordant. The bordism relation splits manifolds
into equivalence classes (see the Figure), which are called
bordism classes.
[edit] 3 Unoriented bordism
We denote the bordism class of  by
by ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) , and denote by
, and denote by
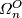 the set of bordism classes of
the set of bordism classes of  -dimensional
manifolds. Then
-dimensional
manifolds. Then 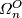 is an abelian group with respect
to the disjoint union operation:
is an abelian group with respect
to the disjoint union operation: ![[M_1]+[M_2]=[M_1\sqcup M_2]](/images/math/3/b/8/3b87653a49a8ea82afbc2c15dc9e95e6.png) .
Zero is represented by the bordism class of an empty set (which is
counted as a manifold in any dimension), or by the bordism class
of any manifold which bounds. We also have
.
Zero is represented by the bordism class of an empty set (which is
counted as a manifold in any dimension), or by the bordism class
of any manifold which bounds. We also have 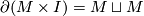 .
Hence,
.
Hence, ![2[M]=0](/images/math/a/1/e/a1eb8e559a8b69ef409bff457991f923.png) and
and 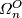 is a 2-torsion group.
is a 2-torsion group.
Set 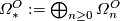 . The
product of bordism classes, namely
. The
product of bordism classes, namely ![[M_1]\times [M_2]=[M_1 \times M_2]](/images/math/b/c/a/bca399878134d24055d89500866ba471.png) , makes
, makes 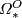 a graded commutative ring known as
the unoriented bordism ring.
a graded commutative ring known as
the unoriented bordism ring.
For any space  the bordism relation can be extended to
maps of
the bordism relation can be extended to
maps of  -dimensional manifolds to
-dimensional manifolds to  : two maps
: two maps 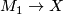 and
and
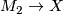 are bordant if there is a bordism
are bordant if there is a bordism 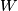 between
between
 and
and 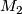 and the map
and the map 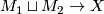 extends to a map
extends to a map
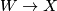 . The set of bordism classes of maps
. The set of bordism classes of maps 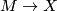 forms an
abelian group called the
forms an
abelian group called the  -dimensional unoriented bordism group of
-dimensional unoriented bordism group of  and denoted
and denoted 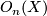 (other notations:
(other notations: 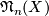 ,
, 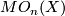 ).
).
The assignment 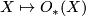 defines a
generalised homology theory, that is, it is functorial in
defines a
generalised homology theory, that is, it is functorial in  , homotopy
invariant, has the excision property and exact sequences of pairs. For this
theory we have
, homotopy
invariant, has the excision property and exact sequences of pairs. For this
theory we have 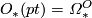 , and
, and 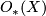 is an
is an
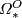 -module.
-module.
The Pontrjagin-Thom construction reduces the calculation of the bordism groups to a homotopical problem:
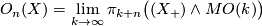
where 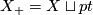 , and
, and 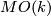 is the Thom space of
the universal vector
is the Thom space of
the universal vector  -plane bundle
-plane bundle 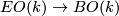 . The
cobordism groups are defined dually:
. The
cobordism groups are defined dually:
![\displaystyle O^n(X)=\lim_{k\to\infty}[\Sigma^{k-n}(X_+),MO(k)]](/images/math/b/b/0/bb05a687d97e200b92528c433a6d0273.png)
where ![[X,Y]](/images/math/e/1/9/e1921829b3d333bdf8227e9d46cb530b.png) denotes the set of based homotopy classes of maps from
denotes the set of based homotopy classes of maps from  to
to  . The resulting generalised cohomology theory is multiplicative, which implies that
. The resulting generalised cohomology theory is multiplicative, which implies that 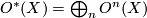 is a graded commutative ring. It follows from the definitions that
is a graded commutative ring. It follows from the definitions that 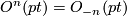 . The graded ring
. The graded ring 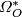 with
with 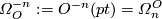 is called the unoriented cobordism ring. It has nonzero elements only in nonpositively graded components. The bordism ring
is called the unoriented cobordism ring. It has nonzero elements only in nonpositively graded components. The bordism ring 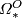 and the cobordism ring
and the cobordism ring 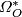 differ only by their gradings, so the notions of the "bordism class" and "cobordism class" of a manifold
differ only by their gradings, so the notions of the "bordism class" and "cobordism class" of a manifold  are interchangeable. The difference between bordism and cobordism appears only when one considers generalised homology and cohomology theories.
are interchangeable. The difference between bordism and cobordism appears only when one considers generalised homology and cohomology theories.
[edit] 4 Oriented and complex bordism
The bordism relation may be extended to manifolds endowed with some additional structure, which leads to the most important examples of bordism theories. The universal homotopical framework for geometric bordism with additional structure is provided by the theory of B-bordism.
The simplest additional structure is an orientation. By definition, two oriented  -dimensional manifolds
-dimensional manifolds  and
and 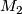 are oriented bordant if there is an oriented
are oriented bordant if there is an oriented 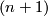 -dimensional manifold
-dimensional manifold  with boundary such that
with boundary such that 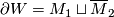 , where
, where 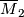 denotes
denotes 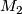 with the orientation reversed. The oriented bordism groups
with the orientation reversed. The oriented bordism groups
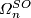 and the oriented bordism ring
and the oriented bordism ring 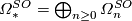 are defined
accordingly. Given an oriented manifold
are defined
accordingly. Given an oriented manifold  , the manifold
, the manifold 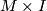 has a canonical orientation such that
has a canonical orientation such that 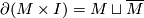 . Hence,
. Hence, ![-[M]=[\overline{M}]](/images/math/5/b/5/5b55530daf53ecbd204d322a03982b78.png) in
in 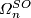 . Unlike
. Unlike 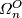 , elements of
, elements of
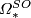 generally do not have order 2.
generally do not have order 2.
Complex structure gives another important example of an additional
structure on manifolds. However, a direct attempt to define the
bordism relation on complex manifolds fails because the manifold
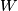 is odd-dimensional and therefore cannot be complex. This can
be remedied by considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) structures.
is odd-dimensional and therefore cannot be complex. This can
be remedied by considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) structures.
Let 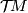 denote the tangent bundle of
denote the tangent bundle of  , and
, and 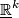 the product vector bundle
the product vector bundle 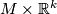 over
over  . A tangential stably complex structure on
. A tangential stably complex structure on  is
determined by a choice of an isomorphism
is
determined by a choice of an isomorphism
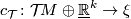
between the "stable" tangent bundle and a complex vector
bundle  over
over  . Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determine the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on
. Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determine the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on  is determined by a choice of a complex bundle
structure on the normal bundle
is determined by a choice of a complex bundle
structure on the normal bundle 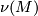 of an embedding
of an embedding
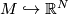 . Tangential and normal stably
complex structures on
. Tangential and normal stably
complex structures on  determine each other by means of the
canonical isomorphism
determine each other by means of the
canonical isomorphism 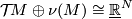 . We therefore may restrict
our attention to tangential structures only.
. We therefore may restrict
our attention to tangential structures only.
A stably complex manifold is a pair 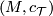 consisting of a manifold
consisting of a manifold  and a stably complex structure
and a stably complex structure
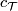 on it. This is a generalisation of a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on
on it. This is a generalisation of a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on 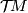 , i.e. a
stably complex structure
, i.e. a
stably complex structure 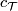 with
with  ).
).
Example 4.1.
Let 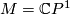 . The standard complex structure on
. The standard complex structure on  is
equivalent to the stably complex structure determined by the
isomorphism
is
equivalent to the stably complex structure determined by the
isomorphism
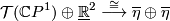
where 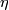 is the Hopf line bundle. On the other hand, the
isomorphism
is the Hopf line bundle. On the other hand, the
isomorphism
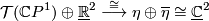
determines a trivial stably complex structure on 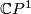 .
.
The bordism relation can be defined between stably complex
manifolds. Like the case of unoriented bordism, the set of
bordism classes ![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) of
of  -dimensional stably complex manifolds is an Abelian group with respect to the disjoint union. This group is called the
-dimensional stably complex manifolds is an Abelian group with respect to the disjoint union. This group is called the  -dimensional complex bordism group and
denoted by
-dimensional complex bordism group and
denoted by 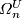 . The zero is represented by the bordism
class of any manifold
. The zero is represented by the bordism
class of any manifold  which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
vector bundle
which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
vector bundle 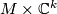 ). The sphere
). The sphere  provides an example
of such a manifold. The opposite element to the bordism class
provides an example
of such a manifold. The opposite element to the bordism class
![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) in the group
in the group 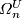 may be
represented by the same manifold
may be
represented by the same manifold  with the stably complex
structure determined by the isomorphism
with the stably complex
structure determined by the isomorphism
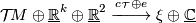
where 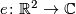 is given by
is given by 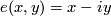 .
.
An abbreviated notation ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) for the complex
bordism class will be used whenever the stably complex structure
for the complex
bordism class will be used whenever the stably complex structure 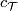 is clear from the context.
is clear from the context.
The complex bordism and cobordism groups of a space
 are defined similarly to the unoriented case:
are defined similarly to the unoriented case:
![\displaystyle \begin{aligned} U_n(X)&=\lim_{k\to\infty}\pi_{2k+n}((X_+)\wedge MU(k)),\\ U^n(X)&=\lim_{k\to\infty}[\Sigma^{2k-n}(X_+),MU(k)] \end{aligned}](/images/math/3/8/8/388203cfec203d491a8ba0f9062a963f.png)
where 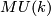 is the Thom space of the universal complex
is the Thom space of the universal complex  -plane
bundle
-plane
bundle 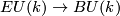 . These groups are
. These groups are 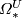 -modules
and give rise to a multiplicative (co)homology theory. In
particular,
-modules
and give rise to a multiplicative (co)homology theory. In
particular, 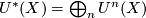 is a graded ring.
is a graded ring.
The graded ring 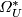 with
with 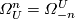 is
called the complex cobordism ring; it has nontrivial
elements only in nonpositively graded components.
is
called the complex cobordism ring; it has nontrivial
elements only in nonpositively graded components.
[edit] 5 Connected sum and bordism
For manifolds of positive dimension the disjoint union 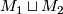 representing the sum of bordism classes
representing the sum of bordism classes ![[M_1]+[M_2]](/images/math/9/b/9/9b9e8d019174b02cdeaf8bc0b13ebc8c.png) may be
replaced by their "connected sum", which represents the same
bordism class.
may be
replaced by their "connected sum", which represents the same
bordism class.
The connected sum 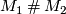 of manifolds
of manifolds  and
and 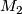 of the same dimension
of the same dimension  is constructed as follows. Choose points
is constructed as follows. Choose points 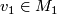 and
and 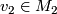 , and take closed
, and take closed  -balls
-balls
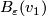 and
and 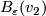 around them (both
manifolds may be assumed to be endowed with a Riemannian metric).
Fix an isometric embedding
around them (both
manifolds may be assumed to be endowed with a Riemannian metric).
Fix an isometric embedding  of a pair of standard
of a pair of standard
 -balls
-balls 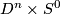 (here
(here 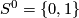 ) into
) into
 which maps
which maps 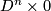 onto
onto 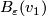 and
and 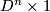 onto
onto 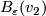 . If both
. If both  and
and 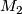 are oriented
we additionally require the embedding
are oriented
we additionally require the embedding  to preserve the
orientation on the first ball and reverse in on the second. Now, using this
embedding, replace in
to preserve the
orientation on the first ball and reverse in on the second. Now, using this
embedding, replace in 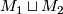 the pair of balls
the pair of balls 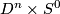 by a "pipe"
by a "pipe" 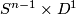 . After smoothing the
angles in the standard way we obtain a smooth manifold
. After smoothing the
angles in the standard way we obtain a smooth manifold 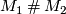 .
.
If both  and
and 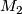 are connected the smooth structure on
are connected the smooth structure on 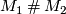 does not depend on a choice
of points
does not depend on a choice
of points 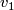 ,
, 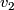 and embedding
and embedding 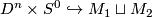 . It does however depend on the orientations;
. It does however depend on the orientations; 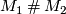 and
and 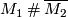 are not diffeomorphic in general.
are not diffeomorphic in general.
There are smooth contraction maps 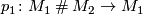 and
and
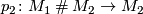 . In the oriented case the manifold
. In the oriented case the manifold
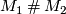 can be oriented in such a way that both contraction
maps preserve the orientations.
can be oriented in such a way that both contraction
maps preserve the orientations.
A bordism between 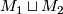 and
and 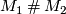 may be
constructed as follows. Consider a cylinder
may be
constructed as follows. Consider a cylinder 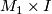 , from
which we remove an
, from
which we remove an  -neighbourhood
-neighbourhood
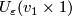 of the point
of the point 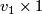 . Similarly,
remove the neighbourhood
. Similarly,
remove the neighbourhood 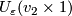 from
from
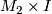 (each of these two neighbourhoods can be identified
with the half of a standard open
(each of these two neighbourhoods can be identified
with the half of a standard open 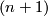 -ball). Now connect the
two remainders of cylinders by a "half pipe"
-ball). Now connect the
two remainders of cylinders by a "half pipe" 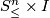 in
such a way that the half-sphere
in
such a way that the half-sphere 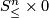 is identified
with the half-sphere on the boundary of
is identified
with the half-sphere on the boundary of
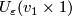 , and
, and 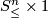 is identified
with the half-sphere on the boundary of
is identified
with the half-sphere on the boundary of 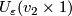 . Smoothening the angles we obtain a manifold with boundary
. Smoothening the angles we obtain a manifold with boundary
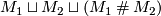 (or
(or
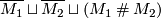 in the
oriented case), see the Figure.
in the
oriented case), see the Figure.
If  and
and 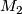 are stably complex manifolds, then
there is a canonical stably complex structure on
are stably complex manifolds, then
there is a canonical stably complex structure on 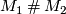 ,
which is constructed as follows. Assume the stably complex
structures on
,
which is constructed as follows. Assume the stably complex
structures on  and
and 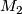 are determined by isomorphisms
are determined by isomorphisms
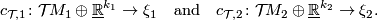
Using the isomorphism 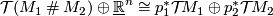 , we define a stably complex structure on
, we define a stably complex structure on
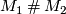 by the isomorphism
by the isomorphism
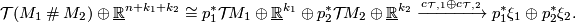
This stably complex structure is called the
connected sum of stably complex structures on  and
and
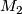 . The corresponding complex bordism class is
. The corresponding complex bordism class is ![[M_1]+[M_2]](/images/math/9/b/9/9b9e8d019174b02cdeaf8bc0b13ebc8c.png) .
.
[edit] 6 Structure results
The theory of unoriented (co)bordism was first to be completed: its coefficient ring 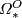 was calculated by Thom, and the bordism groups
was calculated by Thom, and the bordism groups 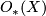 of cell complexes
of cell complexes  were reduced to
homology groups of
were reduced to
homology groups of  with coefficients in
with coefficients in 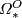 . The
corresponding results are summarised as follows:
. The
corresponding results are summarised as follows:
Theorem 6.1.
- Two manifolds are unorientedly bordant if and only if they have identical sets of Stiefel-Whitney characteristic numbers.
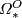 is a polynomial ring over
is a polynomial ring over 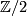 with one generator
with one generator 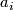 in every positive dimension
in every positive dimension 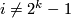 .
.
- For every cell complex
 the module
the module 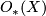 is a free graded
is a free graded 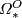 -module isomorphic to
-module isomorphic to 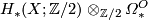 .
.
Parts 1 and 2 were proved in [Thom1954]. Part 3 was proved in [Conner&Floyd1964].
Calculating the complex bordism ring 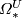 turned out to
be a much more difficult problem:
turned out to
be a much more difficult problem:
Theorem 6.2.
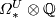 is a polynomial ring over
is a polynomial ring over 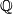 generated by the bordism classes of complex projective spaces
generated by the bordism classes of complex projective spaces 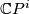 ,
, 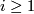 .
.
- Two stably complex manifolds are bordant if and only if they have identical sets of Chern characteristic numbers.
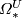 is a polynomial ring over
is a polynomial ring over  with one generator
with one generator 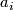 in every even dimension
in every even dimension 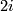 , where
, where 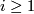 .
.
Part 1 can be proved by the methods of Thom. Part 2 follows from the results of [Milnor1960] and [Novikov1960]. Part 3 is the most difficult one; it was done in 1960 in [Novikov1960] (see also [Novikov1962] for a more detailed account) and Milnor (unpublished, but see [Thom1995]).
Note that part 3 of Theorem 6.1 does not extend to
complex bordism; 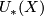 is not a free
is not a free 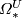 -module in
general. Unlike the case of unoriented bordism, the calculation of complex bordism of a space
-module in
general. Unlike the case of unoriented bordism, the calculation of complex bordism of a space  does not reduce to
calculating the coefficient ring
does not reduce to
calculating the coefficient ring 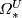 and homology
groups
and homology
groups 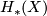 .
.
The calculation of the oriented bordism ring was completed by
[Novikov1960] (ring structure modulo torsion) and [Wall1960] (additive torsion), with important contributions made by
Rokhlin, Averbuch, and Milnor. Unlike complex bordism, the
ring 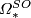 has additive torsion. We give only a partial
result here, which does not fully describe the torsion elements. For the complete description of the ring
has additive torsion. We give only a partial
result here, which does not fully describe the torsion elements. For the complete description of the ring 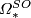 see the Oriented bordism page.
see the Oriented bordism page.
Theorem 6.3.
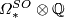 is a polynomial ring over
is a polynomial ring over 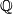 generated by the bordism classes of complex projective spaces
generated by the bordism classes of complex projective spaces 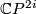 ,
, 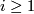 .
.
- The subring
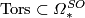 of torsion elements contains only elements of order 2. The quotient
of torsion elements contains only elements of order 2. The quotient 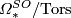 is a polynomial ring over
is a polynomial ring over  with one generator
with one generator 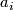 in every dimension
in every dimension 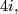 where
where 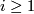 .
.
- Two oriented manifolds are bordant if and only if they have identical sets of Pontrjagin and Stiefel-Whitney characteristic numbers.
For more specific information about the three bordism theories, including constructions of manifolds representing polynomial generators in the bordism rings and applications, see the Unoriented bordism, Oriented bordism, and Complex bordism pages.
[edit] 7 References
- [Atiyah1961] M. F. Atiyah, Bordism and cobordism, Proc. Camb. Philos. Soc. 57 (1961), 200-208. MR0126856 (23 #A4150) Zbl 0104.17405
- [Conner&Floyd1964] P. E. Conner and E. E. Floyd, Differentiable periodic maps, Academic Press Inc., Publishers, New York, 1964. MR0176478 (31 #750) Zbl 0417.57019
- [Milnor1960] J. Milnor, On the cobordism ring
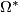 and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
- [Novikov1960] S. P. Novikov, Some problems in the topology of manifolds connected with the theory of Thom spaces, Soviet Math. Dokl. 1 (1960), 717–720. MR0121815 (22 #12545) Zbl 0094.35902
- [Novikov1962] S. P. Novikov, Homotopy properties of Thom complexes, Mat. Sb. (N.S.) 57 (99) (1962), 407–442. MR0157381 (28 #615) Zbl 0193.51801
- [Pontryagin1959] L. S. Pontryagin, Smooth manifolds and their applications in homotopy theory, Amer. Math. Soc. Translations, Ser. 2, Vol. 11, Providence, R.I. (1959), 1–114. MR0115178 (22 #5980) Zbl 0084.19002
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502
- [Thom1995] R. Thom, Travaux de Milnor sur le cobordisme, Séminaire Bourbaki, Vol. 5, Exp. No. 180, Soc. Math. France, Paris, (1995), 169–177. MR1603465 Zbl 0116.40402
- [Wall1960] C. T. C. Wall, Determination of the cobordism ring, Ann. of Math. (2) 72 (1960), 292–311. MR0120654 (22 #11403) Zbl 0097.38801