B-Bordism
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
In this article we recall the definition of the bordism groups of closed manifolds, ususally with extra topological structure: orientation, spin-structure, weak complex structure etc.
We specify the extra structure by a fibration 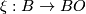 where
where
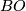 denotes the classifying space of the stable orthogonal group and
denotes the classifying space of the stable orthogonal group and  is homotopy equivalent to a CW complex of finite type. For example the fibrations
is homotopy equivalent to a CW complex of finite type. For example the fibrations 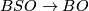 and
and 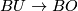 induced by the canonical homomorphisms
induced by the canonical homomorphisms 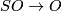 and
and 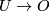 are used for respectively oriented and complex bordism.
are used for respectively oriented and complex bordism.
Abusing notation, one writes  for the fibraion
for the fibraion  : for each
: for each  and
and 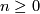 there is a bordism group of closed n-manifolds with
there is a bordism group of closed n-manifolds with  structure denoted
structure denoted
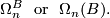
If 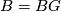 is the classifying space of the stable group
is the classifying space of the stable group  then on often writes
then on often writes
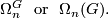
2 Stable vector bundles
We recall the defintion of a stable vector bundle from [Kreck&Lück2005, 18.10] which requires some notation. Let 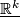 denote the trivial rank k bundle
denote the trivial rank k bundle 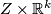 : the space
: the space 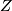 will be clear from context. Let
will be clear from context. Let 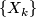 be a sequence
be a sequence 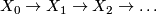 of inclusions
of inclusions 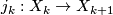 of CW-complexes. A stable vector bundle
of CW-complexes. A stable vector bundle  over
over 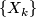 is a sequence of rank k-vector bundles
is a sequence of rank k-vector bundles 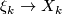 and a sequence of bundle maps
and a sequence of bundle maps
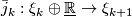
where 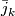 covers the inclusion
covers the inclusion 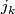 . An isomorphism of stable vector bundles over
. An isomorphism of stable vector bundles over 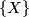 ,
, 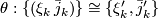 is a sequence of bundle ismorphisms
is a sequence of bundle ismorphisms 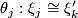 for
for 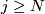 ,
,  some integer, which are compatible with
some integer, which are compatible with 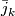 and
and 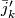 .
.
Here are some important examples:
- A rank
 -vector
-vector 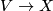 over a CW complex
over a CW complex  defines a stable vector bundle
defines a stable vector bundle 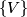 by setting
by setting 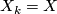 fixed for all
fixed for all  ,
, 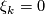 for
for 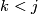 and
and 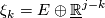 for
for 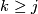 with
with 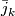 the obvious inclusions.
the obvious inclusions.
- If
 is a compact n-manifold then
is a compact n-manifold then  embedds into
embedds into 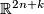 for
for 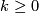 and for
and for 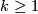 two such embeddings are isotopic. The normal bundle of any such embedding defines a stable vector bundle over
two such embeddings are isotopic. The normal bundle of any such embedding defines a stable vector bundle over  as in the first example and there is a canonical isomorphicm between any two such stable bundles given by isotopies between the embeddings. We write
as in the first example and there is a canonical isomorphicm between any two such stable bundles given by isotopies between the embeddings. We write 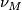 for the stable normal bundle of
for the stable normal bundle of  . Note that by defintion
. Note that by defintion 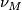 is a stable inverse to the tangent bundle of
is a stable inverse to the tangent bundle of  :
:
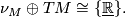
- The universal bundle
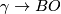 is the stable bundle with
is the stable bundle with 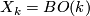 ,
, 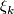 the universal
the universal  -plane bundle and
-plane bundle and 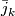 the classifymap of
the classifymap of 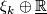 .
.
- If
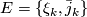 is a stable vector bundle over
is a stable vector bundle over 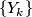 and
and  is a sequence of maps
is a sequence of maps 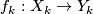 compatible with inclusions then
compatible with inclusions then 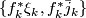 is a stable vector bundle over
is a stable vector bundle over 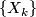 called the pull-back bundle and denoted
called the pull-back bundle and denoted 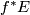 .
.
3 B-manifolds and B-bordism
Let 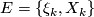 be a stable vector bundle. A normal
be a stable vector bundle. A normal  -manifold is a triple
-manifold is a triple 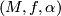 consisting of a compact manifold
consisting of a compact manifold  , a map sequence of maps
, a map sequence of maps 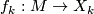 , and a stable bundle isomorphism
, and a stable bundle isomorphism 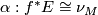 .
.
Recall that 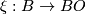 is a fibration. We next define normal
is a fibration. We next define normal  -manifolds and normal
-manifolds and normal  -bordism: more details are given in [Stong1968][Chapter II] and [Kreck1999][Section 1]. If
-bordism: more details are given in [Stong1968][Chapter II] and [Kreck1999][Section 1]. If  is a compact smooth manifold then
is a compact smooth manifold then 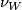 is classified by a map, also denoted
is classified by a map, also denoted 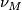 ,
, 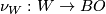 :
: 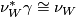 . A
. A  -structure on
-structure on  is a map
is a map 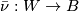 lifting
lifting 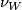 through
through  :
:
![\displaystyle \xymatrix{ & B \ar[d]^{\gamma} \\ W \ar[r]_{\nu_W}\ar[ur]^{\bar \nu} & BO.}](/images/math/c/2/5/c25a11f4d9ccd5c2e076d6d5ea3e9ec9.png)
A  -manifold is a pair
-manifold is a pair 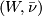 where
where 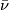 is a
is a  -structure on
-structure on  . If
. If  has boundary
has boundary 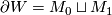 , a disjoint union of two closed
, a disjoint union of two closed  -manifolds with inclusions
-manifolds with inclusions 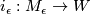 ,
, 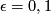 , then
, then  is a
is a  -bordism between the
-bordism between the  -manifolds
-manifolds 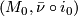 and
and 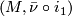 .
.
4 The Pontrjagin Thom isomorphism
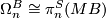
5 Spectral sequences
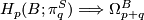
6 References
- [Kreck&Lück2005] M. Kreck and W. Lück, The Novikov conjecture, Birkhäuser Verlag, Basel, 2005. MR2117411 (2005i:19003) Zbl 1058.19001
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010