B-Bordism
(→B-manifolds and B-bordism) |
(→Introduction) |
||
| Line 6: | Line 6: | ||
Associated to each fibration $B$ there is a bordism group of closed n-manifolds with $B$ structure denoted | Associated to each fibration $B$ there is a bordism group of closed n-manifolds with $B$ structure denoted | ||
$$\Omega_n^B ~~\text{or}~~ \Omega_n^G.$$ | $$\Omega_n^B ~~\text{or}~~ \Omega_n^G.$$ | ||
| − | The latter notation is used if $B = BG$ is the classifying space of the group $G$. In this page we review the the defintion bordism of the groups $\Omega_n^B$ and recall some fundamental theorems about | + | The latter notation is used if $B = BG$ is the classifying space of the group $G$. In this page we review the the defintion bordism of the groups $\Omega_n^B$ and recall some fundamental theorems about concerning these groups. |
</wikitex> | </wikitex> | ||
Revision as of 15:11, 8 January 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let 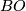 denote the classifying space of the stable orthogonal group and let
denote the classifying space of the stable orthogonal group and let  denote a fibration
denote a fibration 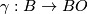 where
where  is homotopy equivalent to a CW complex of finite type. For example, consider
is homotopy equivalent to a CW complex of finite type. For example, consider 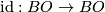 , or the maps
, or the maps 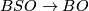 or
or 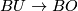 induced by the canonical homomorphisms
induced by the canonical homomorphisms 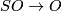 and
and 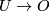 .
.
Associated to each fibration  there is a bordism group of closed n-manifolds with
there is a bordism group of closed n-manifolds with  structure denoted
structure denoted
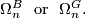
The latter notation is used if 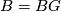 is the classifying space of the group
is the classifying space of the group  . In this page we review the the defintion bordism of the groups
. In this page we review the the defintion bordism of the groups 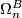 and recall some fundamental theorems about concerning these groups.
and recall some fundamental theorems about concerning these groups.
2 B-manifolds and B-bordism
We briefly recall the defintion of  -manifolds and
-manifolds and  -bordism: more details are given in [Stong1968][Chapter II] and [Kreck1999][Section 1]. If
-bordism: more details are given in [Stong1968][Chapter II] and [Kreck1999][Section 1]. If  is a compact smooth manifold then the stable normal bundle of
is a compact smooth manifold then the stable normal bundle of  is classified by a map
is classified by a map 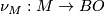 . A
. A  -structure on
-structure on  is a map
is a map 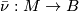 lifting
lifting 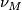 through
through  :
:
![\displaystyle \xymatrix{ & B \ar[d]^{\gamma} \\ M \ar[r]_{\nu_M}\ar[ur]^{\bar \nu} & BO}](/images/math/f/c/2/fc27238a7863c474450c304b8dc569a4.png)
3 The Pontrjagin Thom isomorphism
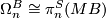
4 Spectral sequences
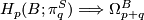
5 References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010