Aspherical manifolds
(→Classification) |
(→Construction and examples) |
||
| Line 12: | Line 12: | ||
* In any dimension, if $M$ admits a metric of non-positive [[Wikipedia:Sectional_curvature|sectional curvature]] then $M$ is aspherical. | * In any dimension, if $M$ admits a metric of non-positive [[Wikipedia:Sectional_curvature|sectional curvature]] then $M$ is aspherical. | ||
* If $L$ is a Lie group with $\pi_0(L)$ finite, $K$ is a maximal compact subgroup of $L$ and $G$ is a discrete torsion free lattice in $L$ then | * If $L$ is a Lie group with $\pi_0(L)$ finite, $K$ is a maximal compact subgroup of $L$ and $G$ is a discrete torsion free lattice in $L$ then | ||
| − | + | $G \backslash L/K$ is aspherical. | |
| − | is aspherical. | + | * A product of aspherical manifolds is again aspherical: |
| + | ** $T^n$, the $n$-torus is aspherical. | ||
</wikitex> | </wikitex> | ||
Revision as of 12:28, 30 November 2009
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:23, 27 September 2012 and the changes since publication. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
A path-connected space  is called aspherical is its higher homotopy groups vanish:
is called aspherical is its higher homotopy groups vanish: 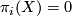 for all
for all 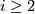 . This article is about closed, aspherical manifolds
. This article is about closed, aspherical manifolds  which are connected manifolds with contractible universal cover
which are connected manifolds with contractible universal cover 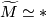 .
.
2 Construction and examples
-
 is aspherical.
is aspherical.
- Any surface
 , not homeomorphic to
, not homeomorphic to  or
or 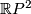 is aspherical.
is aspherical.
- A closed, oriented
 -manifold
-manifold  is aspherical if and only if it is irreducible and
is aspherical if and only if it is irreducible and 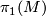 is torsion free.
is torsion free.
- In any dimension, if
 admits a metric of non-positive sectional curvature then
admits a metric of non-positive sectional curvature then  is aspherical.
is aspherical.
- If
 is a Lie group with
is a Lie group with 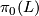 finite,
finite,  is a maximal compact subgroup of
is a maximal compact subgroup of  and
and  is a discrete torsion free lattice in
is a discrete torsion free lattice in  then
then
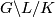 is aspherical.
is aspherical.
- A product of aspherical manifolds is again aspherical:
-
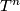 , the
, the Tex syntax error
-torus is aspherical.
-
3 Invariants
The primary invariant of an aspherical manifold  is its fundamental group,
is its fundamental group, 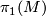 .
.
-
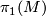 is finitely presented and torsion free.
is finitely presented and torsion free.
-
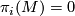 for
for  by definition.
by definition.
As each aspherical manifold  is a
is a 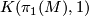 , the homology and cohomology of
, the homology and cohomology of  are by definition the homology and cohomology of
are by definition the homology and cohomology of 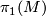 . For any coefficient module
. For any coefficient module  :
:
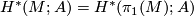 ,
,
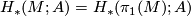 .
.
4 Classification
Two aspherical manifolds  and
and  are homotopy equivalent if and only if there is an isomorphism
are homotopy equivalent if and only if there is an isomorphism 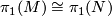 .
.
The main conjecture organising the classification of aspherical manifolds is the Borel Conjecture.
Conjecture 4.1.
Let 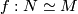 be a homotopy equivalence between aspherical manifolds. Then
be a homotopy equivalence between aspherical manifolds. Then  is homotopic to a homeomorphism.
is homotopic to a homeomorphism.
5 Further discussion
For further information see [Farrell&Jones1990] and [Lück2008].
6 References
- [Farrell&Jones1990] F. T. Farrell and L. E. Jones, Classical aspherical manifolds, Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1990. MR1056079 (91k:57001) Zbl 0729.57001
- [Lück2008] W. Lück, Survey on aspherical manifolds, to appear in the proceedings of the 5-th ECM in Amsterdam (2008).