Aspherical manifolds
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:23, 27 September 2012 and the changes since publication. |
|
The user responsible for this page is Lueck. No other user may edit this page at present. |
1 Introduction
This page is devoted to aspherical closed manifolds.
Definition 1.1.
A space  is called aspherical if it is path connected and all its higher homotopy groups vanish, i.e.,
is called aspherical if it is path connected and all its higher homotopy groups vanish, i.e., 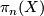 is trivial for
is trivial for 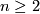 .
.
Aspherical closed manifolds are very interesting objects since there are many examples, intriguing questions and conjectures about them. For instance:
- Interesting geometric constructions or examples lead to aspherical closed manifolds, e.g., non-positively curved closed manifolds, closed surfaces except
 and
and 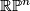 , irreducible closed orientable
, irreducible closed orientable  -manifolds with infinite fundamental groups, locally symmetric spaces arising from almost connected Lie groups and discrete torsionfree cocompact lattices.
-manifolds with infinite fundamental groups, locally symmetric spaces arising from almost connected Lie groups and discrete torsionfree cocompact lattices.
- There are exotic aspherical closed manifolds which do not come from standard constructions and have unexpected properties, e.g., the universal covering is not homeomorphic to
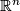 , they are not triangulable. The key construction methods are the reflection trick and hyperbolization.
, they are not triangulable. The key construction methods are the reflection trick and hyperbolization.
- Which groups occur as fundamental groups of aspherical closed manifolds?
- The Borel Conjecture predicts that aspherical closed topological manifolds are topologically rigid, i.e., any homotopy equivalence of aspherical closed manifolds is homotopic to the identity.
- The condition aspherical is of purely homotopy theoretical nature. Nevertheless there are some interesting questions and conjectures such as the Singer Conjecture and the Zero-in-the-Spectrum Conjecture about the spectrum of the Laplace operator on the universal coverings of aspherical closed Riemannian manifolds.
2 Homotopy classification of spaces
From the homotopy theory point of view an aspherical  -complex is completely determined by its fundamental group. Namely,
-complex is completely determined by its fundamental group. Namely,
Theorem 2.1 [Homotopy classification of aspherical spaces].
Two aspherical  -complexes are homotopy equivalent if and only if their fundamental groups are isomorphic.
-complexes are homotopy equivalent if and only if their fundamental groups are isomorphic.
Proof.
By Whitehead's Theorem (see [Whitehead1978, Theorem IV.7.15 on page 182]) a map between  -complexes is a homotopy equivalence if and only if it induces on all homotopy groups bijections. Hence it suffices to construct for two aspherical
-complexes is a homotopy equivalence if and only if it induces on all homotopy groups bijections. Hence it suffices to construct for two aspherical  -complexes
-complexes  and
and  together with an isomorphism
together with an isomorphism 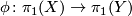 a map
a map 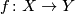 which induces
which induces  on the fundamental groups. Any connected
on the fundamental groups. Any connected  -complex is homotopy equivalent to a
-complex is homotopy equivalent to a  -complex with precisely one
-complex with precisely one  -cell, otherwise collapse a maximal sub-tree of the
-cell, otherwise collapse a maximal sub-tree of the  -skeleton to a point. Hence we can assume without loss of generality that the
-skeleton to a point. Hence we can assume without loss of generality that the  -skeleton of
-skeleton of  is a bouquet of
is a bouquet of  -dimensional spheres. The map
-dimensional spheres. The map  tells us how to define
tells us how to define 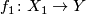 , where
, where 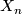 will denote the
will denote the  -skeleton of
-skeleton of 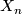 . The composites of the attaching maps for the two-cells of
. The composites of the attaching maps for the two-cells of  with
with  are null-homotopic by the Seifert-van Kampen Theorem. Hence we can extend
are null-homotopic by the Seifert-van Kampen Theorem. Hence we can extend  to a map
to a map 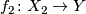 . Since all higher homotopy groups of
. Since all higher homotopy groups of  are trivial, we can extend
are trivial, we can extend 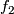 to a map
to a map 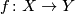 .
.

Lemma 2.2. A  -complex
-complex  is aspherical if and only if it is connected and its universal covering
is aspherical if and only if it is connected and its universal covering  is contractible.
is contractible.
Proof. The projection 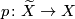 induces isomorphisms on the homotopy groups
induces isomorphisms on the homotopy groups 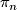 for
for 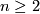 and a connected
and a connected  -complex is contractible if and only if all its homotopy groups are trivial (see [Whitehead1978, Theorem IV.7.15 on page 182]).
-complex is contractible if and only if all its homotopy groups are trivial (see [Whitehead1978, Theorem IV.7.15 on page 182]).

An aspherical  -complex
-complex  with fundamental group
with fundamental group  is the same as an Eilenberg Mac-Lane space
is the same as an Eilenberg Mac-Lane space 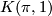 of type
of type 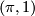 and the same as the classifying space
and the same as the classifying space 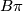 for the group
for the group  .
.
3 Examples of aspherical manifolds
3.1 Non-positive curvature
Let  be a closed smooth manifold. Suppose that it possesses a Riemannian metric whose sectional curvature is non-positive, i.e., is
be a closed smooth manifold. Suppose that it possesses a Riemannian metric whose sectional curvature is non-positive, i.e., is 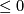 everywhere. Then the universal covering
everywhere. Then the universal covering  inherits a complete Riemannian metric whose sectional curvature is non-positive. Since
inherits a complete Riemannian metric whose sectional curvature is non-positive. Since  is simply-connected and has non-positive sectional curvature, the Hadamard-Cartan Theorem (see [Gallot&Hulin&Lafontaine1987, 3.87 on page 134]) implies that
is simply-connected and has non-positive sectional curvature, the Hadamard-Cartan Theorem (see [Gallot&Hulin&Lafontaine1987, 3.87 on page 134]) implies that  is diffeomorphic to
is diffeomorphic to 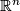 and hence contractible. We conclude that
and hence contractible. We conclude that  and hence
and hence  is aspherical.
is aspherical.
3.2 Low-dimensions
A connected closed  -dimensional manifold is homeomorphic to
-dimensional manifold is homeomorphic to  and hence aspherical.
and hence aspherical.
Let  be a connected closed
be a connected closed  -dimensional manifold. Then
-dimensional manifold. Then  is either aspherical or homeomorphic to
is either aspherical or homeomorphic to  or
or 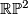 . The following statements are equivalent:
. The following statements are equivalent:
-
 is aspherical.
is aspherical.
-
 admits a Riemannian metric which is flat, i.e., with sectional curvature constant
admits a Riemannian metric which is flat, i.e., with sectional curvature constant  , or which is hyperbolic, i.e., with sectional curvature constant
, or which is hyperbolic, i.e., with sectional curvature constant  .
.
- The universal covering of
 is homeomorphic to
is homeomorphic to 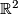 .
.
A connected closed  -manifold
-manifold  is called prime if for any decomposition as a connected sum
is called prime if for any decomposition as a connected sum 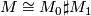 one of the summands
one of the summands  or
or  is homeomorphic to
is homeomorphic to  . It is called irreducible if any embedded sphere
. It is called irreducible if any embedded sphere  bounds a disk
bounds a disk 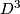 . Every irreducible closed
. Every irreducible closed  -manifold is prime. A prime closed
-manifold is prime. A prime closed  -manifold is either irreducible or an
-manifold is either irreducible or an  -bundle over
-bundle over  (see [Hempel1976, Lemma 3.13 on page 28]). A closed orientable
(see [Hempel1976, Lemma 3.13 on page 28]). A closed orientable  -manifold is aspherical if and only if it is irreducible and has infinite fundamental group. This follows from the Sphere Theorem [Hempel1976, Theorem 4.3 on page 40]. Thurston's Geometrization Conjecture implies that a closed
-manifold is aspherical if and only if it is irreducible and has infinite fundamental group. This follows from the Sphere Theorem [Hempel1976, Theorem 4.3 on page 40]. Thurston's Geometrization Conjecture implies that a closed  -manifold is aspherical if and only if its universal covering is homeomorphic to
-manifold is aspherical if and only if its universal covering is homeomorphic to 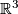 . This follows from [Hempel1976, Theorem 13.4 on page 142] and the fact that the
. This follows from [Hempel1976, Theorem 13.4 on page 142] and the fact that the  -dimensional geometries which have compact quotients and whose underlying topological spaces are contractible have as underlying smooth manifold
-dimensional geometries which have compact quotients and whose underlying topological spaces are contractible have as underlying smooth manifold 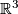 (see [Scott1983]). A proof of Thurston's Geometrization Conjecture is given in [Morgan&Tian2008] following ideas of Perelman. There are examples of closed orientable
(see [Scott1983]). A proof of Thurston's Geometrization Conjecture is given in [Morgan&Tian2008] following ideas of Perelman. There are examples of closed orientable  -manifolds that are aspherical but do not support a Riemannian metric with non-positive sectional curvature (see [Leeb1995]). For more information about
-manifolds that are aspherical but do not support a Riemannian metric with non-positive sectional curvature (see [Leeb1995]). For more information about  -manifolds we refer for instance to [Hempel1976, Scott1983].
-manifolds we refer for instance to [Hempel1976, Scott1983].
3.3 Torsionfree discrete subgroups of almost connected Lie groups
Let  be a Lie group with finitely many path components. Let
be a Lie group with finitely many path components. Let 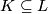 be a maximal compact subgroup. Let
be a maximal compact subgroup. Let 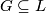 be a discrete torsionfree subgroup. Then
be a discrete torsionfree subgroup. Then 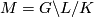 is an aspherical closed manifold with fundamental group
is an aspherical closed manifold with fundamental group  since its universal covering
since its universal covering 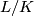 is diffeomorphic to
is diffeomorphic to 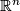 for appropriate
for appropriate  (see [Helgason2001, Theorem 1. in Chapter VI]).
(see [Helgason2001, Theorem 1. in Chapter VI]).
3.4 Products and fibrations
Obviously the product 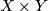 of two aspherical spaces is again aspherical. More generally, if
of two aspherical spaces is again aspherical. More generally, if 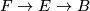 is a fibration for aspherical spaces
is a fibration for aspherical spaces  and
and  , then the long homotopy sequence associated to it shows that
, then the long homotopy sequence associated to it shows that  is aspherical.
is aspherical.
3.5 Pushouts
Let  be a
be a  -complex with sub-
-complex with sub- -complexes
-complexes 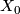 ,
, 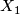 and
and 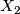 such that
such that 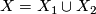 and
and 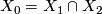 . Suppose that
. Suppose that 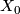 ,
, 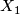 and
and 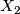 are aspherical and that for
are aspherical and that for 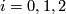 and each base point
and each base point 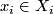 the inclusion induces an injection
the inclusion induces an injection 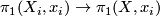 . Then
. Then  is aspherical. The idea of the proof is to check by a Mayer-Vietoris argument that the reduced homology of
is aspherical. The idea of the proof is to check by a Mayer-Vietoris argument that the reduced homology of  is trivial as
is trivial as  is the union of
is the union of 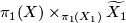 and
and 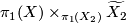 , and
, and 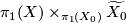 is the intersection of
is the intersection of 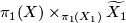 and
and 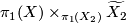 . Hence
. Hence  is contractible by the Hurewicz Theorem (see [Whitehead1978, Theorem IV.7.15 on page 182]).
is contractible by the Hurewicz Theorem (see [Whitehead1978, Theorem IV.7.15 on page 182]).
3.6 Hyperbolization
A very important construction of aspherical closed manifolds comes from the hyperbolization technique due to Gromov [Gromov1987]. It turns a cell complex into a non-positively curved (and hence aspherical) polyhedron. The rough idea is to define this procedure for simplices such that it is natural under inclusions of simplices and then define the hyperbolization of a simplicial complex by gluing the results for the simplices together as described by the combinatorics of the simplicial complex. The goal is to achieve that the result shares some of the properties of the simplicial complexes one has started with, but additionally to produce a non-positively curved and hence aspherical polyhedron. Since this construction preserves local structures, it turns manifolds into manifolds. We briefly explain what the orientable hyperbolization procedure gives. Further expositions of this construction can be found in [Charney&Davis1995, Davis2002, Davis2008, Davis&Januszkiewicz1991]. We start with a finite-dimensional simplicial complex  and assign to it a cubical cell complex
and assign to it a cubical cell complex 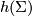 and a natural map
and a natural map 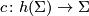 with the following properties:
with the following properties:
-
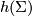 is non-positively curved and in particular aspherical;
is non-positively curved and in particular aspherical;
- The natural map
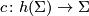 induces a surjection on the integral homology;
induces a surjection on the integral homology;
-
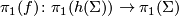 is surjective;
is surjective;
- If
 is an orientable manifold, then
is an orientable manifold, then
-
 is a manifold;
is a manifold;
- The natural map
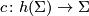 has degree one;
has degree one;
- There is a stable isomorphism between the tangent bundle
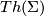 and the pullback
and the pullback 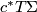 ;
;
3.7 Exotic aspherical closed manifolds
The following result is taken from Davis-Januszkiewicz [Davis&Januszkiewicz1991, Theorem 5a.1].
Theorem 3.1.
There is an aspherical closed  -manifold
-manifold  with the following properties:
with the following properties:
-
 is not homotopy equivalent to a
is not homotopy equivalent to a  -manifold;
-manifold;
-
 is not triangulable, i.e., not homeomorphic to a simplicial complex;
is not triangulable, i.e., not homeomorphic to a simplicial complex;
- The universal covering
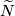 is not homeomorphic to
is not homeomorphic to 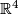 ;
;
-
 is homotopy equivalent to a piecewise flat, non-positively curved polyhedron.
is homotopy equivalent to a piecewise flat, non-positively curved polyhedron.
The next result is due to Davis-Januszkiewicz [Davis&Januszkiewicz1991, Theorem 5a.4].
Theorem 3.2 [Non-PL-example].
For every 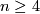 there exists an aspherical closed
there exists an aspherical closed  -manifold which is not homotopy equivalent to a PL-manifold
-manifold which is not homotopy equivalent to a PL-manifold
The proof of the following theorem can be found in [Davis1983], [Davis&Januszkiewicz1991, Theorem 5b.1].
Theorem 3.3 [Exotic universal covering]. For each 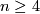 there exists an aspherical closed
there exists an aspherical closed  -dimensional manifold such that its universal covering is not homeomorphic to
-dimensional manifold such that its universal covering is not homeomorphic to 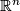 .
.
By the Hadamard-Cartan Theorem (see [Gallot&Hulin&Lafontaine1987, 3.87 on page 134]) the manifold appearing in Theorem 3.3 above cannot be homeomorphic to a smooth manifold with Riemannian metric with non-positive sectional curvature. The following theorem is proved in [Davis&Januszkiewicz1991, Theorem 5c.1 and Remark on page 386] by considering the ideal boundary, which is a quasiisometry invariant in the negatively curved case.
Theorem 3.4 [Exotic example with hyperbolic fundamental group].
For every 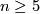 there exists an aspherical closed smooth
there exists an aspherical closed smooth  -dimensional manifold
-dimensional manifold  which is homeomorphic to a strictly negatively curved polyhedron and has in particular a hyperbolic fundamental group such that the universal covering is homeomorphic to
which is homeomorphic to a strictly negatively curved polyhedron and has in particular a hyperbolic fundamental group such that the universal covering is homeomorphic to 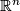 but
but  is not homeomorphic to a smooth manifold with Riemannian metric with negative sectional curvature.
is not homeomorphic to a smooth manifold with Riemannian metric with negative sectional curvature.
The next results are due to Belegradek [Belegradek2006, Corollary 5.1], Mess [Mess1990] and Weinberger (see [Davis2002, Section 13]).
Theorem 3.5 [Exotic fundamental groups].
- For every
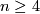 there is an aspherical closed manifold of dimension
there is an aspherical closed manifold of dimension  whose fundamental group contains an infinite divisible abelian group;
whose fundamental group contains an infinite divisible abelian group;
- For every
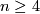 there is an aspherical closed manifold of dimension
there is an aspherical closed manifold of dimension  whose fundamental group has an unsolvable word problem and whose simplicial volume is non-zero.
whose fundamental group has an unsolvable word problem and whose simplicial volume is non-zero.
Notice that a finitely presented group with unsolvable word problem is not a 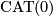 -group, not hyperbolic, not automatic, not asynchronously automatic, not residually finite and not linear over any commutative ring (see [Belegradek2006, Remark 5.2]). The proof of Theorem 3.5 is based on the reflection group trick as it appears for instance in [Davis2002, Sections 8, 10 and 13]. It can be summarized as follows.
-group, not hyperbolic, not automatic, not asynchronously automatic, not residually finite and not linear over any commutative ring (see [Belegradek2006, Remark 5.2]). The proof of Theorem 3.5 is based on the reflection group trick as it appears for instance in [Davis2002, Sections 8, 10 and 13]. It can be summarized as follows.
Theorem 3.6 [Reflection group trick].
Let  be a group which possesses a finite model for
be a group which possesses a finite model for 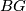 . Then there is an aspherical closed manifold
. Then there is an aspherical closed manifold  and two maps
and two maps 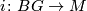 and
and 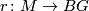 such that
such that 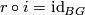 .
.
Remark 3.7 [Reflection group trick and various conjectures].
Another interesting immediate consequence of the reflection group trick is (see also [Davis2002, Sections 11]) that many well-known conjectures about groups hold for every group which possesses a finite model for 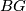 if and only if it holds for the fundamental group of every aspherical closed manifold. This applies for instance to the Kaplansky Conjecture, Unit Conjecture, Zero-divisor-conjecture, Baum-Connes Conjecture, Farrell-Jones Conjecture for algebraic
if and only if it holds for the fundamental group of every aspherical closed manifold. This applies for instance to the Kaplansky Conjecture, Unit Conjecture, Zero-divisor-conjecture, Baum-Connes Conjecture, Farrell-Jones Conjecture for algebraic  -theory for regular
-theory for regular  , Farrell-Jones Conjecture for algebraic
, Farrell-Jones Conjecture for algebraic  -theory, the vanishing of
-theory, the vanishing of 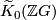 and of
and of 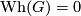 , For information about these conjectures and their links we refer for instance to [Bartels&Lück&Reich2008], [Lück2002] and [Lück&Reich2005]. Further similar consequences of the reflection group trick can be found in Belegradek [Belegradek2006].
, For information about these conjectures and their links we refer for instance to [Bartels&Lück&Reich2008], [Lück2002] and [Lück&Reich2005]. Further similar consequences of the reflection group trick can be found in Belegradek [Belegradek2006].
4 Non-aspherical closed manifolds
A closed manifold of dimension 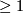 with finite fundamental group is never aspherical. So prominent non-aspherical closed manifolds are spheres, lens spaces, real projective spaces and complex projective spaces.
with finite fundamental group is never aspherical. So prominent non-aspherical closed manifolds are spheres, lens spaces, real projective spaces and complex projective spaces.
Lemma 4.1.
The fundamental group of an aspherical finite-dimensional  -complex
-complex  is torsionfree.
is torsionfree.
Proof.
Let 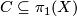 be a finite cyclic subgroup of
be a finite cyclic subgroup of 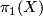 . We have to show that
. We have to show that  is trivial. Since
is trivial. Since  is aspherical,
is aspherical, 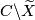 is a finite-dimensional model for
is a finite-dimensional model for 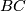 . Hence
. Hence 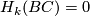 for large
for large  . This implies that
. This implies that  is trivial.
is trivial.

We mention without proof:
Lemma 4.2.
If  is a connected sum
is a connected sum 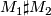 of two closed manifolds
of two closed manifolds  and
and 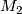 of dimension
of dimension 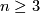 which are not homotopy equivalent to a sphere, then
which are not homotopy equivalent to a sphere, then  is not aspherical.
is not aspherical.
5 Characteristic classes and bordisms of aspherical closed manifolds
Suppose that  is a closed manifold. Then the pullbacks of the characteristic classes of
is a closed manifold. Then the pullbacks of the characteristic classes of  under the natural map
under the natural map 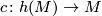 appearing in the Section 3.6 about hyperbolization yield the characteristic classes of
appearing in the Section 3.6 about hyperbolization yield the characteristic classes of 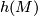 and
and  and
and 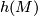 have the same characteristic numbers. This shows that the condition aspherical does not impose any restrictions on the characteristic numbers of a manifold. Consider a bordism theory
have the same characteristic numbers. This shows that the condition aspherical does not impose any restrictions on the characteristic numbers of a manifold. Consider a bordism theory 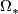 for PL-manifolds or smooth manifolds which is given by imposing conditions on the stable tangent bundle. Examples are unoriented bordism, oriented bordism, framed bordism. Then any bordism class can be represented by an aspherical closed manifold. If two aspherical closed manifolds represent the same bordism class, then one can find an aspherical bordism between them. See [Davis2002, Remarks 15.1], [Davis&Januszkiewicz1991, Theorem B], and [Davis&Januszkiewicz&Weinberger2001].
for PL-manifolds or smooth manifolds which is given by imposing conditions on the stable tangent bundle. Examples are unoriented bordism, oriented bordism, framed bordism. Then any bordism class can be represented by an aspherical closed manifold. If two aspherical closed manifolds represent the same bordism class, then one can find an aspherical bordism between them. See [Davis2002, Remarks 15.1], [Davis&Januszkiewicz1991, Theorem B], and [Davis&Januszkiewicz&Weinberger2001].
6 The Borel Conjecture
Definition 6.1 [Topologically rigid].
We call a closed manifold  topologically rigid if any homotopy equivalence
topologically rigid if any homotopy equivalence 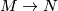 with a closed manifold
with a closed manifold  as source is homotopic to a homeomorphism.
as source is homotopic to a homeomorphism.
The Poincaré Conjecture is equivalent to the statement that any sphere  is topologically rigid.
is topologically rigid.
Conjecture 6.2 [Borel Conjecture].
Every aspherical closed manifold is topologically rigid.
In particular the Borel Conjecture 6.2 implies because of Theorem 2.1 that two aspherical closed manifolds are homeomorphic if and only if their fundamental groups are isomorphic.
Remark 6.3 [The Borel Conjecture in low dimensions].
The Borel Conjecture is true in dimension 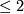 by the classification of closed manifolds of dimension
by the classification of closed manifolds of dimension  . It is true in dimension
. It is true in dimension  if Thurston's Geometrization Conjecture is true. This follows from results of Waldhausen (see Hempel [Hempel1976, Lemma 10.1 and Corollary 13.7]) and Turaev (see [Turaev1988]) as explained for instance in [Kreck&Lück2009, Section 5]. A proof of Thurston's Geometrization Conjecture is given in [Morgan&Tian2008] following ideas of Perelman.
if Thurston's Geometrization Conjecture is true. This follows from results of Waldhausen (see Hempel [Hempel1976, Lemma 10.1 and Corollary 13.7]) and Turaev (see [Turaev1988]) as explained for instance in [Kreck&Lück2009, Section 5]. A proof of Thurston's Geometrization Conjecture is given in [Morgan&Tian2008] following ideas of Perelman.
Remark 6.4 [Topological rigidity for non-aspherical manifolds].
Topological rigidity phenomenons do hold also for some non-aspherical closed manifolds. For instance the sphere  is topologically rigid by the Poincaré Conjecture. The Poincaré Conjecture is known to be true in all dimensions. This follows in high dimensions from the
is topologically rigid by the Poincaré Conjecture. The Poincaré Conjecture is known to be true in all dimensions. This follows in high dimensions from the  -cobordism theorem, in dimension four from the work of Freedman [Freedman1982], in dimension three from the work of Perelman as explained in [Kleiner&Lott2008] and [Morgan&Tian2007] and in dimension two from the classification of surfaces. Many more examples of classes of manifolds which are topologically rigid are given and analyzed in Kreck-Lück [Kreck&Lück2009]. For instance the connected sum of closed manifolds of dimension
-cobordism theorem, in dimension four from the work of Freedman [Freedman1982], in dimension three from the work of Perelman as explained in [Kleiner&Lott2008] and [Morgan&Tian2007] and in dimension two from the classification of surfaces. Many more examples of classes of manifolds which are topologically rigid are given and analyzed in Kreck-Lück [Kreck&Lück2009]. For instance the connected sum of closed manifolds of dimension 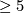 which are topologically rigid and whose fundamental groups do not contain elements of order two, is again topologically rigid and the connected sum of two manifolds is in general not aspherical (see Lemma 4.2). The product
which are topologically rigid and whose fundamental groups do not contain elements of order two, is again topologically rigid and the connected sum of two manifolds is in general not aspherical (see Lemma 4.2). The product 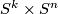 is topologically rigid if and only if
is topologically rigid if and only if  and
and  are odd.
are odd.
Remark 6.5 [The Borel Conjecture does not hold in the smooth category].
The Borel Conjecture 6.2 is false in the smooth category, i.e., if one replaces topological manifold by smooth manifold and homeomorphism by diffeomorphism. The torus 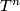 for
for 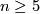 is an example (see [Wall1999, 15A]).
is an example (see [Wall1999, 15A]).
Other interesting counterexamples involving negatively curved manifolds are given
by Farrell-Jones [Farrell&Jones1989, Theorem 0.1]. They construct for every  and
and 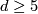 a
a  -dimensional closed hyperbolic manifold
-dimensional closed hyperbolic manifold  and a closed Riemannian manifold
and a closed Riemannian manifold  such that the sectional curvature of
such that the sectional curvature of  is pinched between
is pinched between 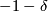 and
and 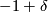 and the manifolds
and the manifolds  and
and  are homeomorphic but not diffeomorphic.
are homeomorphic but not diffeomorphic.
Remark 6.6 [The Borel Conjecture versus Mostow rigidity].
The examples of Farrell-Jones [Farrell&Jones1989, Theorem 0.1] give actually more. Namely, they yield for given  a closed Riemannian manifold
a closed Riemannian manifold  whose sectional curvature lies in the interval
whose sectional curvature lies in the interval ![[1-\epsilon,-1 + \epsilon]](/images/math/0/0/6/00653fd41bf6fe23bfe86de24c6998bc.png) and a closed hyperbolic manifold
and a closed hyperbolic manifold  such that
such that  and
and  are homeomorphic but no diffeomorphic. The idea of the construction is essentially to take the connected sum of
are homeomorphic but no diffeomorphic. The idea of the construction is essentially to take the connected sum of  with exotic spheres. Notice that by definition
with exotic spheres. Notice that by definition  were hyperbolic if we would take
were hyperbolic if we would take 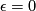 . Hence this example is remarkable in view of Mostow rigidity, which predicts for two closed hyperbolic manifolds
. Hence this example is remarkable in view of Mostow rigidity, which predicts for two closed hyperbolic manifolds  and
and 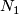 that they are isometrically diffeomorphic if and only if
that they are isometrically diffeomorphic if and only if 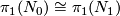 and any homotopy equivalence
and any homotopy equivalence 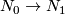 is homotopic to an isometric diffeomorphism. One may view the Borel Conjecture as the topological version of Mostow rigidity. The conclusion in the Borel Conjecture is weaker, one gets only homeomorphisms and not isometric diffeomorphisms, but the assumption is also weaker, since there are many more aspherical closed topological manifolds than hyperbolic closed manifolds.
is homotopic to an isometric diffeomorphism. One may view the Borel Conjecture as the topological version of Mostow rigidity. The conclusion in the Borel Conjecture is weaker, one gets only homeomorphisms and not isometric diffeomorphisms, but the assumption is also weaker, since there are many more aspherical closed topological manifolds than hyperbolic closed manifolds.
Remark 6.7 [The work of Farrell-Jones].
Farrell-Jones have made deep contributions to the Borel Conjecture. They have proved it in dimension 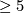 for non-positively curved closed Riemannian manifolds, for compact complete affine flat manifolds and for aspherical closed manifolds whose fundamental group is isomorphic to the fundamental group of a complete non-positively curved Riemannian manifold which is A-regular (see [Farrell&Jones1990, Farrell&Jones1991, Farrell&Jones1993, Farrell&Jones1998]).
for non-positively curved closed Riemannian manifolds, for compact complete affine flat manifolds and for aspherical closed manifolds whose fundamental group is isomorphic to the fundamental group of a complete non-positively curved Riemannian manifold which is A-regular (see [Farrell&Jones1990, Farrell&Jones1991, Farrell&Jones1993, Farrell&Jones1998]).
The following result is a consequence of [Bartels&Farrell&Lück2011, Bartels&Lück2012, Bartels&Lück&Reich&Rüping2012].
Theorem 6.8.
Let 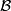 be the smallest class of groups satisfying:
be the smallest class of groups satisfying:
- Every hyperbolic group belongs to
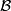 ;
;
- Every
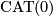 -group, i.e., a group that acts properly, isometrically and cocompactly on a complete proper
-group, i.e., a group that acts properly, isometrically and cocompactly on a complete proper 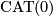 -space, belongs to
-space, belongs to 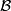 ;
;
- Every cocompact lattice in an almost connected Lie group belongs to
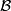 ;
;
- Every arithmetic group over an algebraic number field belongs to
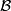 ;
;
- If
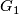 and
and 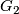 belong to
belong to  , then both
, then both 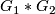 and
and 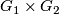 belong to
belong to 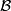 ;
;
- If
 is a subgroup of
is a subgroup of  and
and 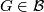 , then
, then 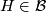 ;
;
- Let
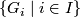 be a directed system of groups (with not necessarily injective structure maps) such that
be a directed system of groups (with not necessarily injective structure maps) such that 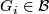 for every
for every 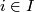 . Then the directed colimit
. Then the directed colimit 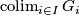 belongs to
belongs to 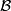 .
.
Then every aspherical closed manifold of dimension 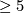 whose fundamental group belongs to
whose fundamental group belongs to 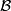 is topologically rigid.
is topologically rigid.
Actually, Bartels and Lück [Bartels&Lück2012] prove the Farrell-Jones Conjecture about the algebraic  - and
- and  -theory of group rings which does imply the claim appearing in Theorem 6.8 by surgery theory.
-theory of group rings which does imply the claim appearing in Theorem 6.8 by surgery theory.
Remark 6.9 [Exotic aspherical closed manifolds].
Theorem 6.8 implies that the exotic aspherical manifolds mentioned in Subsection 3.7 satisfy the Borel Conjecture in dimension 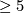 since their universal coverings are
since their universal coverings are 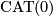 -spaces.
-spaces.
Remark 6.10 [Directed colimits of hyperbolic groups].
There are also a variety of interesting groups such as lacunary groups in the sense of Ol'shanskii-Osin-Sapir [Ol'shanskii&Osin&Sapir2009] or groups with expanders as they appear in the counterexample to the Baum-Connes Conjecture with coefficients due to Higson-Lafforgue-Skandalis [Higson&Lafforgue&Skandalis2002] and which have been constructed by Arzhantseva-Delzant [Arzhantseva&Delzant2008, Theorem 7.11 and Theorem 7.12] following ideas of Gromov [Gromov2003]. Since these arise as colimits of directed systems of hyperbolic groups, they do satisfy the Farrell-Jones Conjecture and the Borel Conjecture in dimension 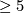 by Bartels and Lück [Bartels&Lück2012]. The Bost Conjecture has also been proved for colimits of hyperbolic groups by Bartels-Echterhoff-Lück [Bartels&Echterhoff&Lück2008].
by Bartels and Lück [Bartels&Lück2012]. The Bost Conjecture has also been proved for colimits of hyperbolic groups by Bartels-Echterhoff-Lück [Bartels&Echterhoff&Lück2008].
7 Poincaré duality groups
In this section we deal with the question when a group  is the fundamental group of an aspherical closed manifold. The following definition is due to Johnson-Wall [Johnson&Wall1972].
is the fundamental group of an aspherical closed manifold. The following definition is due to Johnson-Wall [Johnson&Wall1972].
Definition 7.1 [Poincaré duality group].
A group  is called a Poincaré duality group of dimension
is called a Poincaré duality group of dimension  if the following conditions holds:
if the following conditions holds:
- The group
 is of type FP, i.e., the trivial
is of type FP, i.e., the trivial 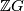 -module
-module  possesses a finite-dimensional projective
possesses a finite-dimensional projective 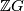 -resolution by finitely generated projective
-resolution by finitely generated projective 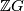 -modules;
-modules;
- We get an isomorphism of abelian groups
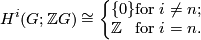
Conjecture 7.2 [Poincaré duality groups].
A finitely presented group is a  -dimensional Poincaré duality group if and only if it is the fundamental group of an aspherical closed
-dimensional Poincaré duality group if and only if it is the fundamental group of an aspherical closed  -dimensional topological manifold.
-dimensional topological manifold.
A topological space  is called an absolute neighborhood retract or briefly
is called an absolute neighborhood retract or briefly 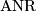 if for every normal space
if for every normal space 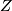 , every closed subset
, every closed subset 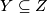 and every (continuous) map
and every (continuous) map 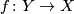 there exists an open neighborhood
there exists an open neighborhood  of
of  in
in 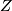 together with an extension
together with an extension 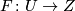 of
of  to
to  . A compact
. A compact  -dimensional homology
-dimensional homology 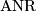 -manifold
-manifold  is a compact absolute neighborhood retract such that it has a countable basis for its topology, has finite topological dimension and for every
is a compact absolute neighborhood retract such that it has a countable basis for its topology, has finite topological dimension and for every 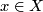 the abelian group
the abelian group 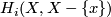 is trivial for
is trivial for 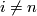 and infinite cyclic for
and infinite cyclic for 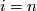 . A closed
. A closed  -dimensional topological manifold is an example of a compact
-dimensional topological manifold is an example of a compact  -dimensional homology
-dimensional homology 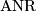 -manifold (see [Daverman1986, Corollary 1A in V.26 page 191]). For a proof of the next result we refer to [Lück2010, Section 5].
-manifold (see [Daverman1986, Corollary 1A in V.26 page 191]). For a proof of the next result we refer to [Lück2010, Section 5].
Theorem 7.3.
Suppose that the torsionfree group  belongs to the class
belongs to the class 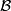 occurring in Theorem 6.8 and its cohomological dimension is
occurring in Theorem 6.8 and its cohomological dimension is 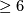 . Then
. Then  is the fundamental group of an aspherical compact homology
is the fundamental group of an aspherical compact homology 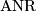 -manifold.
-manifold.
Remark 7.4 [Compact homology 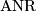 -manifolds versus closed topological manifolds].
-manifolds versus closed topological manifolds].
One would prefer if in the conclusion of Theorem 7.3 one could replace "compact homology 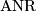 -manifold" by "closed topological manifold". There are compact homology
-manifold" by "closed topological manifold". There are compact homology 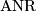 -manifolds that are not homotopy equivalent to closed manifolds. But no example of an aspherical compact homology
-manifolds that are not homotopy equivalent to closed manifolds. But no example of an aspherical compact homology 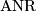 -manifold that is not homotopy equivalent to a closed topological manifold is known.
-manifold that is not homotopy equivalent to a closed topological manifold is known.
The Borel Conjecture about the topologically rigidity of closed topological manifolds
and the fact that it is implied by the Farrell-Jones Conjecture indimensions 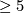 carry
over to compact homology
carry
over to compact homology 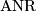 -manifolds
if one replaces "being homotopic to a homeomorphism" by "being
-manifolds
if one replaces "being homotopic to a homeomorphism" by "being  -cobordant to a homeomorphism".
-cobordant to a homeomorphism".
We refer for instance to [Bryant&Ferry&Mio&Weinberger1996, Ferry&Pedersen1995, Quinn1983, Quinn1987, Ranicki1992] for more information about this topic.
8 Product decompositions
In this section we show that, roughly speaking, an aspherical closed manifold  is a product
is a product 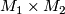 if and only if its fundamental group is a product
if and only if its fundamental group is a product 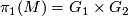 and that such a decomposition is unique up to homeomorphism. A proof of the next result can be found in [Lück2010, Section 6].
and that such a decomposition is unique up to homeomorphism. A proof of the next result can be found in [Lück2010, Section 6].
Theorem 8.1 [Product decomposition].
Let be an aspherical closed manifold of dimension
be an aspherical closed manifold of dimension  with fundamental group
with fundamental group 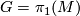 . Suppose we have a product decomposition
. Suppose we have a product decomposition 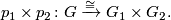
 ,
, 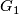 and
and 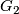 belong to the class
belong to the class 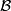 occurring in Theorem 6.8. Assume that the cohomological dimension
occurring in Theorem 6.8. Assume that the cohomological dimension 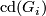 is different from
is different from  ,
,  and
and 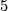 for
for 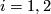 and
and 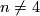 . Then:
. Then:
- There are aspherical closed topological manifolds
 and
and 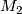 together with isomorphisms and maps
together with isomorphisms and maps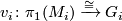 for
for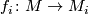
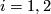 such that is a homeomorphism and
such that is a homeomorphism and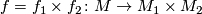
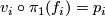 (up to inner automorphisms) for
(up to inner automorphisms) for 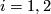 ;
;
- Suppose we have another such choice of aspherical closed manifolds
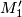 and
and 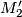 together with isomorphisms and maps
together with isomorphisms and maps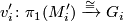 for
for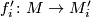
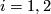 such that the map
such that the map 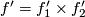 is a homotopy equivalence and
is a homotopy equivalence and 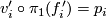 (up to inner automorphisms) for
(up to inner automorphisms) for 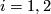 . Then there are for
. Then there are for 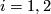 homeomorphisms
homeomorphisms 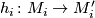 such that
such that 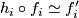 and
and 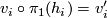 holds for
holds for 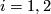 .
.
Remark 8.2 [Product decompositions and non-positive sectional curvature].
The following result has been proved independently by Gromoll-Wolf [Gromoll&Wolf1971, Theorem 2] and Lawson-Yau [Lawson&Yau1972].
Let  be a closed Riemannian manifold with non-positive sectional curvature. Suppose that we are given a splitting of its fundamental group
be a closed Riemannian manifold with non-positive sectional curvature. Suppose that we are given a splitting of its fundamental group 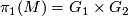 and that the center of
and that the center of 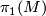 is trivial. Then this splitting comes from an isometric product decomposition of closed Riemannian manifolds of non-positive sectional curvature
is trivial. Then this splitting comes from an isometric product decomposition of closed Riemannian manifolds of non-positive sectional curvature 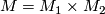 .
.
9 The Novikov Conjecture
Let
 be a group and let
be a group and let 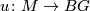 be a map from a closed oriented smooth manifold
be a map from a closed oriented smooth manifold  to
to 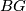 . Let
. Let 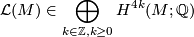
 -class of
-class of  . Its
. Its  -th entry
-th entry 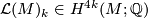 is a certain homogeneous polynomial of degree
is a certain homogeneous polynomial of degree  in the rational Pontrjagin classes
in the rational Pontrjagin classes 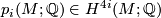 for
for 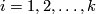 such that the coefficient
such that the coefficient 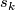 of the monomial
of the monomial 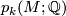 is different from zero. The
is different from zero. The  -class
-class 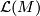 is determined by all the rational Pontrjagin classes and vice versa. The
is determined by all the rational Pontrjagin classes and vice versa. The  -class depends on the tangent bundle and thus on the differentiable structure of
-class depends on the tangent bundle and thus on the differentiable structure of  . For
. For 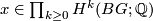 define the higher signature of
define the higher signature of  associated to
associated to  and
and  to be the integer
to be the integer ![\displaystyle \begin{array}{rcl} \operatorname{sign}_x(M,u) & := & \langle \mathcal{L}(M) \cup f^* x,[M] \rangle. \end{array}](/images/math/e/5/f/e5f24580532eca318a58b99c3a8bc71d.png)
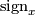 for
for 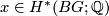 is homotopy invariant if for two closed oriented smooth manifolds
is homotopy invariant if for two closed oriented smooth manifolds  and
and  with reference maps
with reference maps 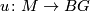 and
and 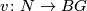 we have
we have 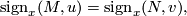
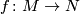 such that
such that 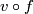 and
and  are homotopic. If
are homotopic. If 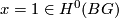 , then the higher signature
, then the higher signature 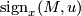 is by the Hirzebruch signature formula (see [Hirzebruch1958, Hirzebruch1971]) the signature of
is by the Hirzebruch signature formula (see [Hirzebruch1958, Hirzebruch1971]) the signature of  itself and hence an invariant of the oriented homotopy type. This is one motivation for the following conjecture.
itself and hence an invariant of the oriented homotopy type. This is one motivation for the following conjecture.
Conjecture 9.1 [Novikov Conjecture].
Let  be a group. Then
be a group. Then 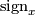 is homotopy invariant for all
is homotopy invariant for all 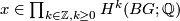 .
.
This conjecture appears for the first time in the paper by Novikov [Novikov1970, §11]. A survey about its history can be found in [Ferry&Ranicki&Rosenberg1995b]. More information can be found for instance in [Ferry&Ranicki&Rosenberg1995, Ferry&Ranicki&Rosenberg1995a, Kreck&Lück2005].
Remark 9.2 [The Novikov Conjecture and aspherical closed manifolds].
Let the map 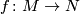 be a homotopy equivalence of aspherical closed oriented manifolds. Then the Novikov Conjecture 9.1
implies that
be a homotopy equivalence of aspherical closed oriented manifolds. Then the Novikov Conjecture 9.1
implies that 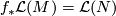 . This is certainly true if
. This is certainly true if  is a diffeomorphism. On the other hand, in general the rational Pontrjagin classes are not homotopy invariants and the integral Pontrjagin classes
is a diffeomorphism. On the other hand, in general the rational Pontrjagin classes are not homotopy invariants and the integral Pontrjagin classes 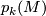 are not homeomorphism invariants (see for instance [Kreck&Lück2005, Example 1.6 and Theorem 4.8]). This seems to shed doubts about the Novikov Conjecture. However, if the Borel Conjecture is true, the map
are not homeomorphism invariants (see for instance [Kreck&Lück2005, Example 1.6 and Theorem 4.8]). This seems to shed doubts about the Novikov Conjecture. However, if the Borel Conjecture is true, the map 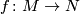 is homotopic to a homeomorphism and the conclusion
is homotopic to a homeomorphism and the conclusion 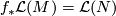 does follow from the following deep result due to Novikov [Novikov1965a, Novikov1965, Novikov1966].
does follow from the following deep result due to Novikov [Novikov1965a, Novikov1965, Novikov1966].
Theorem 9.3 [Topological invariance of rational Pontrjagin classes].
The rational Pontrjagin classes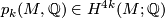 are topological invariants, i.e. for a homeomorphism
are topological invariants, i.e. for a homeomorphism 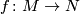 of closed smooth manifolds we have
of closed smooth manifolds we have 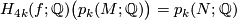
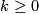 and in particular
and in particular 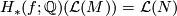 .
.
Remark 9.4 [Positive scalar curvature].
There is the conjecture that a closed aspherical smooth manifold does not carry a metric of positive scalar curvature. One evidence for it is the fact that it is implied by the (strong) Novikov Conjecture see [Rosenberg1983, Theorem 3.5].
10 Boundaries of hyperbolic groups
We mention the following result of Bartels-Lück-Weinberger [Bartels&Lück&Weinberger2010]. For the notion of the boundary of a hyperbolic group and its main properties we refer for instance to [Kapovich&Benakli2002].
Theorem 10.1.
Let  be a torsion-free hyperbolic group and let
be a torsion-free hyperbolic group and let  be an integer
be an integer 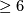 . Then the following statements are equivalent:
. Then the following statements are equivalent:
- The boundary
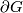 is homeomorphic to
is homeomorphic to 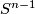 ;
;
- There is an aspherical closed topological manifold
 such that
such that 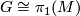 , its universal covering
, its universal covering  is homeomorphic to
is homeomorphic to 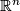 and the compactification of
and the compactification of  by
by 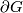 is homeomorphic to
is homeomorphic to 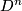 ;
;
- The aspherical closed topological manifold
 appearing in the assertion above is unique up to homeomorphism.
appearing in the assertion above is unique up to homeomorphism.
In general the boundary of a hyperbolic group is not locally a Euclidean space but has a fractal behavior. If the boundary 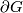 of an infinite hyperbolic group
of an infinite hyperbolic group  contains an open subset homeomorphic to Euclidean
contains an open subset homeomorphic to Euclidean  -space, then it is homeomorphic to
-space, then it is homeomorphic to  . This is proved in [Kapovich&Benakli2002, Theorem 4.4], where more information about the boundaries of hyperbolic groups can be found. For every
. This is proved in [Kapovich&Benakli2002, Theorem 4.4], where more information about the boundaries of hyperbolic groups can be found. For every 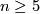 there exists a strictly negatively curved polyhedron of dimension
there exists a strictly negatively curved polyhedron of dimension  whose fundamental group
whose fundamental group  is hyperbolic, which is homeomorphic to an aspherical closed smooth manifold and whose universal covering is homeomorphic to
is hyperbolic, which is homeomorphic to an aspherical closed smooth manifold and whose universal covering is homeomorphic to 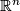 , but the boundary
, but the boundary 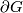 is not homeomorphic to
is not homeomorphic to 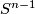 , see [Davis&Januszkiewicz1991, Theorem 5c.1 on page 384 and Remark on page 386]. Thus the condition that
, see [Davis&Januszkiewicz1991, Theorem 5c.1 on page 384 and Remark on page 386]. Thus the condition that 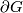 is a sphere for a torsion-free hyperbolic group is (in high dimensions) not equivalent to the existence of an aspherical closed manifold whose fundamental group is
is a sphere for a torsion-free hyperbolic group is (in high dimensions) not equivalent to the existence of an aspherical closed manifold whose fundamental group is  .
.
Remark 10.2 [The Cannon Conjecture].
We do not get information in dimensions 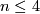 for the usual problems about surgery. In the case
for the usual problems about surgery. In the case 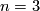 there is the conjecture of Cannon [Cannon1991] that a group
there is the conjecture of Cannon [Cannon1991] that a group  acts properly, isometrically and cocompactly on the
acts properly, isometrically and cocompactly on the  -dimensional hyperbolic plane
-dimensional hyperbolic plane 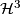 if and only if it is a hyperbolic group whose boundary is homeomorphic to
if and only if it is a hyperbolic group whose boundary is homeomorphic to  . Provided that the infinite hyperbolic group
. Provided that the infinite hyperbolic group  occurs as the fundamental group of a closed irreducible
occurs as the fundamental group of a closed irreducible  -manifold, Bestvina-Mess [Bestvina&Mess1991, Theorem 4.1] have shown that its universal covering is homeomorphic to
-manifold, Bestvina-Mess [Bestvina&Mess1991, Theorem 4.1] have shown that its universal covering is homeomorphic to 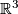 and its compactification by
and its compactification by 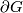 is homeomorphic to
is homeomorphic to 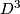 , and the Geometrization Conjecture of Thurston implies that
, and the Geometrization Conjecture of Thurston implies that  is hyperbolic and
is hyperbolic and  satisfies Cannon's conjecture. The problem is solved in the case
satisfies Cannon's conjecture. The problem is solved in the case 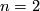 , namely, for a hyperbolic group
, namely, for a hyperbolic group  its boundary
its boundary 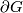 is homeomorphic to
is homeomorphic to  if and only if
if and only if  is a Fuchsian group (see [Casson&Jungreis1994, Freden1995, Gabai1991]).
is a Fuchsian group (see [Casson&Jungreis1994, Freden1995, Gabai1991]).
11 L2-invariants
Next we mention some prominent conjectures about aspherical closed manifolds and  -invariants of their universal coverings. For more information about these conjectures and their status we refer to [Lück2002] and [Lück2009].
-invariants of their universal coverings. For more information about these conjectures and their status we refer to [Lück2002] and [Lück2009].
11.1 The Hopf and the Singer Conjectures
Conjecture 11.1 [Hopf Conjecture].
If is an aspherical closed manifold of even dimension, then
is an aspherical closed manifold of even dimension, then 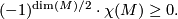
 is a closed Riemannian manifold of even dimension with sectional curvature
is a closed Riemannian manifold of even dimension with sectional curvature 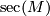 , then
, then 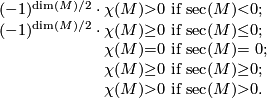
Conjecture 11.2 [Singer Conjecture].
If is an aspherical closed manifold, then
is an aspherical closed manifold, then 
 is a closed connected Riemannian manifold with negative sectional curvature, then
is a closed connected Riemannian manifold with negative sectional curvature, then 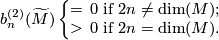
11.2 L2-torsion and aspherical closed manifolds
Conjecture 11.3 [ -torsion for aspherical closed manifolds].
-torsion for aspherical closed manifolds].
 is an aspherical closed manifold of odd dimension, then
is an aspherical closed manifold of odd dimension, then  is
is 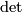 -
- -acyclic and
-acyclic and 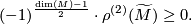
 is a closed connected Riemannian manifold of odd dimension with negative sectional curvature, then
is a closed connected Riemannian manifold of odd dimension with negative sectional curvature, then  is
is 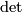 -
- -acyclic and
-acyclic and 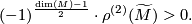
 is an aspherical closed manifold whose fundamental group contains an amenable infinite normal subgroup, then
is an aspherical closed manifold whose fundamental group contains an amenable infinite normal subgroup, then  is
is 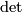 -
- -acyclic and
-acyclic and 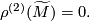
11.3 Homological growth and L2-torsion for closed aspherical manifolds
The following conjecture is motivated by [Lück2002, Conjecture 11.3 on page 418] and in particular by the preprint of Bergeron and Venkatesh [Bergeron&Venkatesh2010, Conjecture 1.3].
Conjecture 11.4 [Homological growth and  -torsion for aspherical manifolds].
-torsion for aspherical manifolds].
Let  be a closed aspherical manifold of dimension
be a closed aspherical manifold of dimension  . Let
. Let
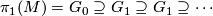
be a nested sequence of in  normal subgroups of finite index
normal subgroups of finite index ![[G:G_i]](/images/math/f/2/a/f2a30fa5acf299fc0fa3a04697e48f8f.png) such that their intersection
such that their intersection
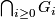 is the trivial subgroup. Then:
is the trivial subgroup. Then:
![\displaystyle \begin{array}{rcl} \lim_{i \in I} \;\frac{\ln\big(\bigl|\operatorname{tors}\bigl(H_n(G_i\backslash \widetilde{M};\mathbb{Z})\bigr)\bigr|\bigr)}{[G:G_i]} & = & 0 \quad \text{if}\;\; 2n+1 \not= \dim(M);\\ \lim_{i \in I} \;\frac{\ln\big(\bigl|\operatorname{tors}\bigl(H_n(G_i\backslash \widetilde{M};\mathbb{Z})\bigr)\bigr|\bigr)}{[G:G_i]} & = & (-1)^p \cdot \rho^{(2)}\bigl(\widetilde{M}\bigr) \quad \text{if}\;\; 2n + 1 = \dim(M). \end{array}](/images/math/b/1/3/b131ccd7c3f8b19087cc720b7773d8ef.png)
If 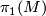 is residually finite, then Conjecture 11.4
implies Conjecture 11.3. Conjecture 11.4
has been proved in the special case, where
is residually finite, then Conjecture 11.4
implies Conjecture 11.3. Conjecture 11.4
has been proved in the special case, where 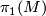 contains an infinite normal elementary amenable subgroup or
contains an infinite normal elementary amenable subgroup or  carries a non-trivial
carries a non-trivial  -action,
in [Lück2012]. A very interesting open case is the one of a closed hyperbolic
-action,
in [Lück2012]. A very interesting open case is the one of a closed hyperbolic  -manifold.
-manifold.
11.4 Q versus Fp-approximation
Conjecture 11.5 [Approximation by Betti numbers].
Let be a closed aspherical manifold of dimension
be a closed aspherical manifold of dimension  . Let
. Let 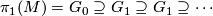
 normal subgroups of finite index
normal subgroups of finite index ![[G:G_i]](/images/math/f/2/a/f2a30fa5acf299fc0fa3a04697e48f8f.png) such that their intersection
such that their intersection 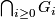 is the trivial subgroup. Let
is the trivial subgroup. Let  be any field. Then we get for every
be any field. Then we get for every 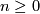
![\displaystyle b_n^{(2)}(\widetilde{M}) = \lim_{i \to \infty} \frac{b_n(G_i\backslash \widetilde{M};K)}{[G:G_i]}.](/images/math/c/c/f/ccf2f48722da3aee987cd2c352b2fee6.png)
Remark 11.6.
Conjecture 11.5 follows from [Lück1994] in the case that  has characteristic zero, actually without the assumption that
has characteristic zero, actually without the assumption that  is aspherical. The interesting and open case is the case of the prime characteristic
is aspherical. The interesting and open case is the case of the prime characteristic  , where the assumption "aspherical" is definitely necessary, see for instance [Bergeron&Linnell&Lück&Sauer2012], [Ershof&Lück2012] and [Linnell&Lück&Sauer2011], and one may additionally demand that each index
, where the assumption "aspherical" is definitely necessary, see for instance [Bergeron&Linnell&Lück&Sauer2012], [Ershof&Lück2012] and [Linnell&Lück&Sauer2011], and one may additionally demand that each index ![[G:G_i]](/images/math/f/2/a/f2a30fa5acf299fc0fa3a04697e48f8f.png) is a
is a  -power.
-power.
11.5 Simplicial volume and L2-invariants
Conjecture 11.7 [Simplicial volume and  -invariants].
-invariants].
 be an aspherical closed orientable manifold. Suppose that its simplicial volume
be an aspherical closed orientable manifold. Suppose that its simplicial volume 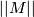 vanishes. Then
vanishes. Then  is of determinant class and
is of determinant class and 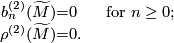
11.6 The Zero-in-the-Spectrum Conjecture
Conjecture 11.8 [Zero-in-the-spectrum Conjecture].
Let be a complete Riemannian manifold. Suppose that
be a complete Riemannian manifold. Suppose that  is the universal covering of an aspherical closed Riemannian manifold
is the universal covering of an aspherical closed Riemannian manifold  (with the Riemannian metric coming from
(with the Riemannian metric coming from  ). Then for some
). Then for some 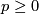 zero is in the Spectrum of the minimal closure
zero is in the Spectrum of the minimal closure 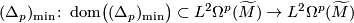
 -forms on
-forms on  .
.
Remark 11.9 [Non-aspherical counterexamples to the Zero-in-the-Spectrum Conjecture].
For all of the conjectures about aspherical spaces stated in this article it is obvious that they cannot be true if one drops the condition aspherical except for the zero-in-the-Spectrum Conjecture 11.8. Farber and Weinberger [Farber&Weinberger2001] gave the first example of a closed Riemannian manifold for which zero is not in the spectrum of the minimal closure 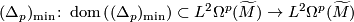 of the Laplacian acting on smooth
of the Laplacian acting on smooth  -forms on
-forms on  for each
for each 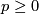 . The construction by Higson, Roe and Schick [Higson&Roe&Schick2001] yields plenty of such counterexamples. But there are no aspherical counterexamples known.
. The construction by Higson, Roe and Schick [Higson&Roe&Schick2001] yields plenty of such counterexamples. But there are no aspherical counterexamples known.
12 References
- [Arzhantseva&Delzant2008] G. Arzhantseva and T. Delzant, Examples of random groups, preprint (2008).
- [Bartels&Echterhoff&Lück2008] A. Bartels, S. Echterhoff and W. Lück, Inheritance of Isomorphism Conjectures under colimits, K-theory and noncommutative geometry, EMS Ser. Congr. Rep., Eur. Math. Soc., Zürich, (2008) 41–70. MR2513332 Zbl 1159.19005
- [Bartels&Farrell&Lück2011] A. Bartels, F. Farrell and W. Lück, The Farrell-Jones Conjecture for cocompact lattices in virtually connected Lie groups, (2011). Available at the arXiv:1101.0469v1.
- [Bartels&Lück&Reich&Rüping2012] A. Bartels, W. Lück, H. Reich and H. Rüping, K- and L-theory of group rings over GL_n(Z), (2012). Available at the arXiv:1204.2418v1.
- [Bartels&Lück&Reich2008] A. Bartels, W. Lück and H. Reich, On the Farrell-Jones Conjecture and its applications, Journal of Topology 1 (2008), 57–86. MR2365652 (2008m:19001) Zbl 1141.19002
- [Bartels&Lück&Weinberger2010] A. Bartels, W. Lück and S. Weinberger, On hyperbolic groups with spheres as boundary, J. Differential Geom. 86 (2010), no.1, 1–16. MR2772544 (2012b:57003) Zbl 1216.53043
- [Bartels&Lück2012] A. Bartels and W. Lück, The Borel conjecture for hyperbolic and CAT(0)-groups., Ann. of Math. (2) 175 (2012), 631–689. MR2993750 Zbl 06025000
- [Belegradek2006] I. Belegradek, Aspherical manifolds, relative hyperbolicity, simplicial volume and assembly maps, Algebr. Geom. Topol. 6 (2006), 1341–1354 (electronic). MR2253450 (2007f:57004) Zbl 1137.20035
- [Bergeron&Linnell&Lück&Sauer2012] N. Bergeron, P. Linnell, W. Lück and R. Sauer, On the growth of Betti numbers in
 -adic analytic towers, (2012). Available at the arXiv:1204.3298v1.
-adic analytic towers, (2012). Available at the arXiv:1204.3298v1.
- [Bergeron&Venkatesh2010] N. Bergeron and A. Venkatesh, The asymptotic growth of torsion homology for arithmetic groups, (2010). Available at the arXiv:1004.1083v1.
- [Bestvina&Mess1991] M. Bestvina and G. Mess, The boundary of negatively curved groups, J. Amer. Math. Soc. 4 (1991), no.3, 469–481. MR1096169 (93j:20076) Zbl 0767.20014
- [Bryant&Ferry&Mio&Weinberger1996] J. Bryant, S. Ferry, W. Mio and S. Weinberger, Topology of homology manifolds, Ann. of Math. (2) 143 (1996), no.3, 435–467. MR1394965 (97b:57017) Zbl 0867.57016
- [Cannon1991] J. W. Cannon, The theory of negatively curved spaces and groups, Ergodic theory, symbolic dynamics, and hyperbolic spaces (Trieste, 1989), Oxford Univ. Press (1991), 315–369. MR1130181 () Zbl 0764.57002
- [Casson&Jungreis1994] A. Casson and D. Jungreis, Convergence groups and Seifert fibered
 -manifolds, Invent. Math. 118 (1994), no.3, 441–456. MR1296353 (96f:57011) Zbl 0840.57005
-manifolds, Invent. Math. 118 (1994), no.3, 441–456. MR1296353 (96f:57011) Zbl 0840.57005
- [Charney&Davis1995] R. M. Charney and M. W. Davis, Strict hyperbolization, Topology 34 (1995), no.2, 329–350. MR1318879 (95m:57034) Zbl 0826.53040
- [Daverman1986] R. J. Daverman, Decompositions of manifolds, Academic Press Inc., 1986. MR872468 (88a:57001) Zbl 1130.57001
- [Davis&Januszkiewicz&Weinberger2001] M. W. Davis, T. Januszkiewicz and S. Weinberger, Relative hyperbolization and aspherical bordisms: an addendum to "Hyperbolization of polyhedra" [J. Differential Geom. 34 (1991), no. 2, 347-388; MR1131435 (92h:57036) by Davis and Januszkiewicz], J. Differential Geom. 58 (2001), no.3, 535–541. MR1906785 (2003e:57038) Zbl 1028.57020
- [Davis&Januszkiewicz1991] M. W. Davis and T. Januszkiewicz, Hyperbolization of polyhedra, J. Differential Geom. 34 (1991), no.2, 347–388. MR1906785 (2003e:57038) Zbl 1028.57020
- [Davis1983] M. W. Davis, Groups generated by reflections and aspherical manifolds not covered by Euclidean space, Ann. of Math. (2) 117 (1983), no.2, 293–324. MR690848 (86d:57025) Zbl 0531.57041
- [Davis2002] M. Davis, Exotic aspherical manifolds, Abdus Salam International Centre for Theoretical Physics, Trieste, 2002. MR1937019 (2004a:57031) Zbl 1070.57012
- [Davis2008] M. W. Davis, The geometry and topology of Coxeter groups, London Mathematical Society Monographs Series, 32. Princeton University Press, Princeton, NJ, 2008. MR2360474 (2008k:20091) Zbl 1142.20020
- [Ershof&Lück2012] M. Ershov and W. Lück, The first
 -Betti number and approximation in arbitrary characteristic, (2012). Available at the arXiv:1206.0474v1.
-Betti number and approximation in arbitrary characteristic, (2012). Available at the arXiv:1206.0474v1.
- [Farber&Weinberger2001] M. Farber and S. Weinberger, On the zero-in-the-spectrum conjecture, Ann. of Math. (2) 154 (2001), no.1, 139–154. MR1847591 (2003b:58044) Zbl 0992.58012
- [Farrell&Jones1989] F. T. Farrell and L. E. Jones, Negatively curved manifolds with exotic smooth structures, J. Amer. Math. Soc. 2 (1989), no.4, 899–908. MR1002632 (90f:53075) Zbl 0698.53027
- [Farrell&Jones1990] F. T. Farrell and L. E. Jones, Classical aspherical manifolds, Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1990. MR1056079 (91k:57001) Zbl 0729.57001
- [Farrell&Jones1991] F. T. Farrell and L. E. Jones, Rigidity in geometry and topology, Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990), 653–663, Math. Soc. Japan, Tokyo, 1991. MR1159252 (93g:57041) Zbl 0745.57008
- [Farrell&Jones1993] F. T. Farrell and L. E. Jones, Topological rigidity for compact non-positively curved manifolds, Differential geometry: Riemannian geometry (Los Angeles, CA, 1990), Proc. Sympos. Pure Math., 54, Part 3, Amer. Math. Soc., Providence, RI, (1993), 229–274. MR1216623 (94m:57067) Zbl 0796.53043
- [Farrell&Jones1998] F. T. Farrell and L. E. Jones, Rigidity for aspherical manifolds with
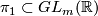 , Asian J. Math. 2 (1998), no.2, 215–262. MR1639544 (99j:57032)Zbl 0912.57012
, Asian J. Math. 2 (1998), no.2, 215–262. MR1639544 (99j:57032)Zbl 0912.57012
- [Ferry&Pedersen1995] S. C. Ferry and E. K. Pedersen, Epsilon surgery theory, Novikov conjectures, index theorems and rigidity, Vol. 2 (Oberwolfach, 1993), Cambridge Univ. Press (1995), 167–226. MR1388311 (97g:57044) Zbl 0956.57020
- [Ferry&Ranicki&Rosenberg1995] S. C. Ferry, A. A. Ranicki and J. Rosenberg, Novikov conjectures, index theorems and rigidity. Vol. 1. London Math. Soc. Lecture Note Ser., 226, Cambridge Univ. Press, Cambridge, 1995. MR1388294 (96m:57002) Zbl 0829.00027
- [Ferry&Ranicki&Rosenberg1995a] S. C. Ferry, A. A. Ranicki and J. Rosenberg, Novikov conjectures, index theorems and rigidity. Vol. 2, London Math. Soc. Lecture Note Ser., 227, Cambridge Univ. Press, Cambridge, 1995. MR1388306 (96m:57003) Zbl 0829.00028
- [Ferry&Ranicki&Rosenberg1995b] S. C. Ferry, A. A. Ranicki and J. Rosenburg, A history and survey of the Novikov conjecture in Ferry&Ranicki&Rosenberg1995 7–66, London Math. Soc. Lecture Note Ser., 226, Cambridge Univ. Press, Cambridge, 1995. MR1388295 (97f:57036) Zbl 0954.57018
- [Freden1995] E. M. Freden, Negatively curved groups have the convergence property. I, Ann. Acad. Sci. Fenn. Ser. A I Math. 20 (1995), no.2, 333–348. MR1346817 (96g:20054) Zbl 0847.20031
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Gabai1991] D. Gabai, Convergence groups are Fuchsian groups, Bull. Amer. Math. Soc. (N.S.) 25 (1991), no.2, 395-402. MR1189862 (93m:20065) Zbl 0785.57004
- [Gallot&Hulin&Lafontaine1987] S. Gallot, D. Hulin and J. Lafontaine, Riemannian geometry, Springer-Verlag, 1987. MR2088027 (2005e:53001) Zbl 1068.53001
- [Gromoll&Wolf1971] D. Gromoll and J. A. Wolf, Some relations between the metric structure and the algebraic structure of the fundamental group in manifolds of nonpositive curvature, Bull. Amer. Math. Soc. 77 (1971), 545–552. MR0281122 (43 #6841) Zbl 0237.53037
- [Gromov1987] M. Gromov, Hyperbolic groups, Essays in group theory,Math. Sci. Res. Inst. Publ., 8, Springer, New York, (1987) 75–263. MR0919829 (89e:20070) Zbl 0634.20015
- [Gromov2003] M. Gromov, Random walk in random groups, Geom. Funct. Anal. 13 (2003), no.1, 73–146. MR1978492 (2004j:20088a) Zbl 1122.20021
- [Helgason2001] S. Helgason, Differential geometry, Lie groups, and symmetric spaces, Corrected reprint of the 1978 original. Graduate Studies in Mathematics, 34. American Mathematical Society, Providence, RI, 2001. MR1834454 (2002b:53081) Zbl 0993.53002
- [Hempel1976] J. Hempel,
 -Manifolds, Princeton University Press, Princeton, N. J., 1976. MR0415619 (54 #3702) Zbl 1058.57001
-Manifolds, Princeton University Press, Princeton, N. J., 1976. MR0415619 (54 #3702) Zbl 1058.57001
- [Higson&Lafforgue&Skandalis2002] N. Higson, V. Lafforgue and G. Skandalis, Counterexamples to the Baum-Connes conjecture, Geom. Funct. Anal. 12 (2002), no.2, 330–354. MR1911663 (2003g:19007) Zbl 1014.46043
- [Higson&Roe&Schick2001] N. Higson, J. Roe and T. Schick, Spaces with vanishing
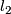 -homology and their fundamental groups (after Farber and Weinberger), Geom. Dedicata 87 (2001), no.1-3, 335–343. MR1866855 (2002m:57031) Zbl 991.57002
-homology and their fundamental groups (after Farber and Weinberger), Geom. Dedicata 87 (2001), no.1-3, 335–343. MR1866855 (2002m:57031) Zbl 991.57002
- [Hirzebruch1958] F. Hirzebruch, Automorphe Formen und der Satz von Riemann-Roch 1958 Symposium internacional de topología algebraica International symposium on algebraic topology, Universidad Nacional Autónoma de México and UNESCO, Mexico City,(1958) 129–144 MR0103280 (21 #2058) Zbl 0129.29801
- [Hirzebruch1971] F. Hirzebruch, The signature theorem: reminiscences and recreation, Prospects in mathematics (Proc. Sympos., Princeton Univ., Princeton, N.J., 1970), Ann. of Math. Studies, No. 70, Princeton Univ. Press, Princeton, N.J. (1971) 3–31. MR0368023 (51 #4265) Zbl 0252.58009
- [Johnson&Wall1972] F. E. A. Johnson and C. T. C. Wall, On groups satisfying Poincaré duality, Ann. of Math. (2) 96 (1972), 592–598. MR0311796 (47 #358) Zbl 0245.57005
- [Kapovich&Benakli2002] I. Kapovich and N. Benakli, Boundaries of hyperbolic groups, in Combinatorial and geometric group theory (New York, 2000/Hoboken, NJ, 2001), Contemp. Math., 296, Amer. Math. Soc., Providence, RI, (2002) 39–93. MR1921706 (2004e:20075) Zbl 1044.20028
- [Kleiner&Lott2008] B. Kleiner and J. Lott, Notes on Perelman's papers, Geom. Topol. 12 (2008), no. 5, 2587–2855. MR2460872 (2010h:53098) Zbl 05530173
- [Kreck&Lück2005] M. Kreck and W. Lück, The Novikov conjecture, Birkhäuser Verlag, Basel, 2005. MR2117411 (2005i:19003) Zbl 1058.19001
- [Kreck&Lück2009] M. Kreck and W. Lück, Topological rigidity for non-aspherical manifolds, Pure Appl. Math. Q. 5 (2009), no.3, Special Issue: In honor of Friedrich Hirzebruch., 873–914. MR2532709 (2010g:57026) Zbl 1196.57018
- [Lawson&Yau1972] J. Lawson and S. T. Yau, Compact manifolds of nonpositive curvature, J. Differential Geometry 7 (1972), 211–228. MR0334083 (48 #12402) Zbl 0266.53035
- [Leeb1995] B. Leeb,
 -manifolds with(out) metrics of nonpositive curvature, Invent. Math. 122 (1995), no.2, 277–289. MR1358977 (97g:57015) Zbl 0840.53031
-manifolds with(out) metrics of nonpositive curvature, Invent. Math. 122 (1995), no.2, 277–289. MR1358977 (97g:57015) Zbl 0840.53031
- [Linnell&Lück&Sauer2011] P. Linnell, W. Lück and R. Sauer, The limit of
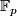 -Betti numbers of a tower of finite covers with amenable fundamental groups, Proc. Amer. Math. Soc. 139 (2011), no.2, 421–434. MR2736326 (2012a:55016) Zbl 1272.55006
-Betti numbers of a tower of finite covers with amenable fundamental groups, Proc. Amer. Math. Soc. 139 (2011), no.2, 421–434. MR2736326 (2012a:55016) Zbl 1272.55006
- [Lück&Reich2005] W. Lück and H. Reich, The Baum-Connes and the Farrell-Jones conjectures in
 - and
- and  -theory, Handbook of K-theory. Vol. 1, 2, 703–842, Springer, Berlin, 2005. MR2181833 (2006k:19012) Zbl 1120.19001
-theory, Handbook of K-theory. Vol. 1, 2, 703–842, Springer, Berlin, 2005. MR2181833 (2006k:19012) Zbl 1120.19001
- [Lück1994] W. Lück, Approximating
 -invariants by their finite-dimensional analogues, Geom. Funct. Anal. 4 (1994), no.4, 455–481. MR1280122 (95g:58234) Zbl 0853.57021
-invariants by their finite-dimensional analogues, Geom. Funct. Anal. 4 (1994), no.4, 455–481. MR1280122 (95g:58234) Zbl 0853.57021
- [Lück2002] W. Lück,
 -invariants: theory and applications to geometry and
-invariants: theory and applications to geometry and  -theory, Springer-Verlag, Berlin, 2002. MR1926649 (2003m:58033) Zbl 1009.55001
-theory, Springer-Verlag, Berlin, 2002. MR1926649 (2003m:58033) Zbl 1009.55001
- [Lück2009] W. Lück,
 -invariants from the algebraic point of view, Geometric and cohomological methods in group theory, Cambridge Univ. Press (2009), 63–161. MR2605176 (2011f:46090) Zbl 1259.57001
-invariants from the algebraic point of view, Geometric and cohomological methods in group theory, Cambridge Univ. Press (2009), 63–161. MR2605176 (2011f:46090) Zbl 1259.57001
- [Lück2010] W. Lück, Survey on aspherical manifolds, European Congress of Mathematics, Eur. Math. Soc., Zürich (2010), 53–82. MR2648321 (2011d:57061) Zbl 1215.57001
- [Lück2012] W. Lück, Approximating L^2-invariants and homology growth, (2012). Available at the arXiv:1203.2827v2.
- [Mess1990] G. Mess, Examples of Poincaré duality groups, Proc. Amer. Math. Soc. 110 (1990), no.4, 1145–1146. MR1019274 (91c:20075) Zbl 0709.57025
- [Morgan&Tian2007] J. Morgan and G. Tian, Ricci flow and the Poincaré conjecture, Clay Mathematics Monographs, 3. American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2007 MR2334563 (2008d:57020) Zbl 1179.57045
- [Morgan&Tian2008] J. Morgan and G. Tian, Completion of the Proof of the Geometrization Conjecture, (2008). Available at the arXiv:0809.4040.
- [Novikov1965] S. P. Novikov, Rational Pontrjagin classes. Homeomorphism and homotopy type of closed manifolds. I, Izv. Akad. Nauk SSSR Ser. Mat. 29 (1965), 1373–1388. MR0196764 (33 #4950) Zbl 0146.19601
- [Novikov1965a] S. P. Novikov, Topological invariance of rational classes of Pontrjagin, Dokl. Akad. Nauk SSSR 163 (1965), 298–300. MR0193644 (33 #1860) Zbl 0146.19502
- [Novikov1966] S. P. Novikov, On manifolds with free abelian fundamental group and their application, Izv. Akad. Nauk SSSR Ser. Mat. 30 (1966), 207–246.
- [Novikov1970] S. P. Novikov, Algebraic construction and properties of Hermitian analogs of
 -theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes. I. II, Math. USSR-Izv. 4 (1970), 257–292; ibid. 4 (1970), 479–505; translated from Izv. Akad. Nauk SSSR Ser. Mat. 34 (1970), 253–288; ibid. 34 (1970), 475. MR0292913 (45 #1994) Zbl 0216.45003 Zbl 0233.57009
-theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes. I. II, Math. USSR-Izv. 4 (1970), 257–292; ibid. 4 (1970), 479–505; translated from Izv. Akad. Nauk SSSR Ser. Mat. 34 (1970), 253–288; ibid. 34 (1970), 475. MR0292913 (45 #1994) Zbl 0216.45003 Zbl 0233.57009
- [Ol'shanskii&Osin&Sapir2009] A. Y. Ol'shanskii, D. V. Osin and M. V. Sapir, Lacunary hyperbolic groups, Geom. Topol. 13 (2009), no.4, 2051–2140. MR2507115 (2010i:20045) Zbl 1243.20056
- [Quinn1983] F. Quinn, Resolutions of homology manifolds, and the topological characterization of manifolds, Invent. Math. 72 (1983), no.2, 267–284. MR700771 (85b:57023) Zbl 0603.57008
- [Quinn1987] F. Quinn, An obstruction to the resolution of homology manifolds, Michigan Math. J. 34 (1987), no.2, 285–291. MR894878 (88j:57016) Zbl 0652.57011
- [Ranicki1992] A. A. Ranicki, Algebraic
 -theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
-theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
- [Rosenberg1983] J. Rosenberg,
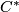 -algebras, positive scalar curvature, and the Novikov conjecture, Inst. Hautes Études Sci. Publ. Math. (1983), no.58, 197–212 (1984). MR720934 (85g:58083) Zbl 0658.53039
-algebras, positive scalar curvature, and the Novikov conjecture, Inst. Hautes Études Sci. Publ. Math. (1983), no.58, 197–212 (1984). MR720934 (85g:58083) Zbl 0658.53039
- [Scott1983] P. Scott, The geometries of
 -manifolds, Bull. London Math. Soc. 15 (1983), no.5, 401–487. MR705527 (84m:57009) Zbl 0662.57001
-manifolds, Bull. London Math. Soc. 15 (1983), no.5, 401–487. MR705527 (84m:57009) Zbl 0662.57001
- [Turaev1988] V. G. Turaev, Homeomorphisms of geometric three-dimensional manifolds, (Russian). Mat. Zametki 43 (1988), no.4, 533–542, 575; translation in Math. Notes 43 (1988), no. 3-4, 307–312. MR940851 (89f:57015) Zbl 0646.57008
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003
- [Whitehead1978] G. W. Whitehead, Elements of homotopy theory, Graduate Texts in Mathematics, 61. Springer-Verlag, New York-Berlin, 1978. MR516508 (80b:55001) Zbl 0406.55001
13 External links
The Wikipedia page on aspherical spaces.