Aspherical manifolds
(→Construction and examples) |
(→Invariants) |
||
| Line 29: | Line 29: | ||
== Invariants == | == Invariants == | ||
<wikitex>; | <wikitex>; | ||
| − | + | The primary invariant of an aspherical manifold $M$ is its fundamental group, $\pi_1(M)$. | |
| + | * $\pi_1(M)$ is finitely presented and torsion free. | ||
| + | * $\pi_i(M) = 0$ for $i > 1$ by definition. | ||
| + | Two aspherical manifolds $M$ and $N$ are homotopy equivalent if and only if there is an isomorphism $\pi_1(M) \cong \pi_1(N)$. | ||
| + | |||
| + | As each aspherical manifold $M$ is a $K(\pi_1(M), 1)$, the homology and cohomology of $M$ are by definition the homology and cohomology of $\pi_1(M)$. For any coefficient module $A$ | ||
| + | $$H^*(M; A) = H^*(\pi_1(M); A)~~~H_*(M;A) = H_*(\pi_1(M); A).$$ | ||
</wikitex> | </wikitex> | ||
Revision as of 12:08, 30 November 2009
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:23, 27 September 2012 and the changes since publication. |
Contents |
1 Introduction
A path-connected space  is called aspherical is its higher homotopy groups vanish:
is called aspherical is its higher homotopy groups vanish: 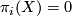 for all
for all 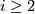 . This article is about closed, aspherical manifolds
. This article is about closed, aspherical manifolds  which are connected manifolds with contractible universal cover
which are connected manifolds with contractible universal cover 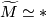 .
.
2 Construction and examples
-
 is aspherical.
is aspherical.
- Any surface
 , not homeomorphic to
, not homeomorphic to  or
or 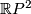 is aspherical.
is aspherical.
- A closed, oriented
 -manifold
-manifold  is aspherical if and only if it is irreducible and
is aspherical if and only if it is irreducible and 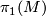 is torsion free.
is torsion free.
- In any dimension, if
 admits a metric of non-positive sectional curvature then
admits a metric of non-positive sectional curvature then  is aspherical.
is aspherical.
- If
 is a Lie group with
is a Lie group with 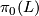 finite,
finite,  is a maximal compact subgroup of
is a maximal compact subgroup of  and
and  is a discrete torsion free lattice in
is a discrete torsion free lattice in  then
then
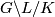
is aspherical.
3 Invariants
The primary invariant of an aspherical manifold  is its fundamental group,
is its fundamental group, 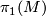 .
.
-
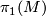 is finitely presented and torsion free.
is finitely presented and torsion free.
-
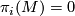 for
for  by definition.
by definition.
Two aspherical manifolds  and
and  are homotopy equivalent if and only if there is an isomorphism
are homotopy equivalent if and only if there is an isomorphism 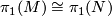 .
.
As each aspherical manifold  is a
is a 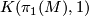 , the homology and cohomology of
, the homology and cohomology of  are by definition the homology and cohomology of
are by definition the homology and cohomology of 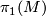 . For any coefficient module
. For any coefficient module 

4 Classification/Characterization (if available)
YOUR TEXT HERE ...
5 Further discussion
YOUR TEXT HERE ...
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |