Aspherical manifolds
(Difference between revisions)
(→Introduction) |
(→Construction and examples) |
||
| Line 18: | Line 18: | ||
== Construction and examples == | == Construction and examples == | ||
<wikitex>; | <wikitex>; | ||
| + | * $S^1$ is aspherical. | ||
| + | * Any [[Surface|surface]] $F$, not homeomorphic to $S^2$ or $\Rr P^2$ is aspherical. | ||
| + | * A closed, oriented $3$-manifold $M$ is aspherical if and only if it is [[irreducible]] and $\pi_1(M)$ is torsion free. | ||
| + | * In any dimension, if $M$ admits a metric of non-positive [[Wikipedia:Sectional_curvature|sectional curvature]] then $M$ is aspherical. | ||
| + | * If $L$ is a Lie group with $\pi_0L)$ finite, $K$ is a maximal compact subgroup of $L$ and $L$ is a discrete torsion free lattice in $L$ then | ||
$$K \backslash G/L$$ | $$K \backslash G/L$$ | ||
| − | + | is aspherical. | |
</wikitex> | </wikitex> | ||
Revision as of 12:03, 30 November 2009
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:23, 27 September 2012 and the changes since publication. |
Contents |
1 Introduction
A path-connected space  is called aspherical is its higher homotopy groups vanish:
is called aspherical is its higher homotopy groups vanish: 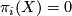 for all
for all 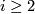 . This article is about closed, aspherical manifolds
. This article is about closed, aspherical manifolds  which are connected manifolds with contractible universal cover
which are connected manifolds with contractible universal cover 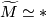 .
.
2 Construction and examples
-
 is aspherical.
is aspherical.
- Any surface
 , not homeomorphic to
, not homeomorphic to  or
or 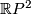 is aspherical.
is aspherical.
- A closed, oriented
 -manifold
-manifold  is aspherical if and only if it is irreducible and
is aspherical if and only if it is irreducible and 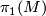 is torsion free.
is torsion free.
- In any dimension, if
 admits a metric of non-positive sectional curvature then
admits a metric of non-positive sectional curvature then  is aspherical.
is aspherical.
- If
 is a Lie group with
is a Lie group with 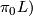 finite,
finite,  is a maximal compact subgroup of
is a maximal compact subgroup of  and
and  is a discrete torsion free lattice in
is a discrete torsion free lattice in  then
then
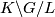
is aspherical.
3 Invariants
YOUR TEXT HERE ...
4 Classification/Characterization (if available)
YOUR TEXT HERE ...
5 Further discussion
YOUR TEXT HERE ...
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |