Almost framed bordism (Ex)
(Created page with "<wikitex>; A closed almost framed $n$-manifold is a closed smooth $n$-manifold $M$ together with a stable framing of its tangent bundle away from a point $x \in M$: that is, a...") |
m |
||
| (3 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | A closed almost framed $n$-manifold is a closed smooth $n$-manifold $M$ together with a stable framing of its tangent bundle away from a point $x \in M$: that is, a | + | A closed almost framed $n$-manifold is a closed smooth $n$-manifold $M$ together with a stable framing of its tangent bundle away from a point $x \in M$: that is, a bundle isomorphism |
| + | $$ TM|_{M-x}\times \Rr^{a} \cong (M - x) \times \Rr^{n+a}$$ | ||
| + | for some $a > 0$. A bordism of closed almost framed manifolds $M_0$ and $M_1$ is a smooth bordism $(W; M_0, M_1)$, a nicely embedded arc $I \subset W$ from $x_0$ and $x_1$ and a stable framing of $TW$ away from $I$: see \cite{Lück2001|Defintions 6.8 & 6.9} for more details. | ||
| − | The set of bordism classes of closed almost framed $n$-manifolds forms a group under connected sum (at the unframed point) and this group is denoted $\Omega_n^{\text{alm}}$ | + | The set of bordism classes of closed almost framed $n$-manifolds forms a group under connected sum (at the unframed point) and this group is denoted $\Omega_n^{\text{alm}}$. There is an obvious forgetful homomorphism |
$$ f \colon \Omega_n^{\text{fr}} \to \Omega_n^{\text{alm}} $$ | $$ f \colon \Omega_n^{\text{fr}} \to \Omega_n^{\text{alm}} $$ | ||
which lies in a sequence | which lies in a sequence | ||
| Line 9: | Line 11: | ||
The task of this exercise is to prove that this sequence is exact: this is the statement of \cite{Lück2001|Lemma 6.16} and may also be found in \cite{Levine1983|Appendix (ii)}. The homomorphisms $\bar J$ and $\partial$ are described in \cite{Lück2001|6.14 & 6.15}. | The task of this exercise is to prove that this sequence is exact: this is the statement of \cite{Lück2001|Lemma 6.16} and may also be found in \cite{Levine1983|Appendix (ii)}. The homomorphisms $\bar J$ and $\partial$ are described in \cite{Lück2001|6.14 & 6.15}. | ||
| − | '''Hint''': Use the [[J-homomorphism]] and [[Pontrjagin-Thom]] construction for framed bordism as explained after the \cite{Lück2001|Lemma 6.16} see also \cite{Lück2001|Definition 6.23 and Lemma 6.24}. | + | '''Hint''': Use the [[J-homomorphism]] and the [[Pontrjagin-Thom]] construction for framed bordism as explained after the \cite{Lück2001|Lemma 6.16} see also \cite{Lück2001|Definition 6.23 and Lemma 6.24}. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
| + | [[Category:Exercises without solution]] | ||
Latest revision as of 09:01, 1 April 2012
A closed almost framed  -manifold is a closed smooth
-manifold is a closed smooth  -manifold
-manifold  together with a stable framing of its tangent bundle away from a point
together with a stable framing of its tangent bundle away from a point 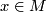 : that is, a bundle isomorphism
: that is, a bundle isomorphism
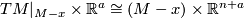
for some 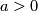 . A bordism of closed almost framed manifolds
. A bordism of closed almost framed manifolds 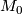 and
and  is a smooth bordism
is a smooth bordism 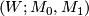 , a nicely embedded arc
, a nicely embedded arc 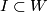 from
from 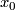 and
and 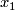 and a stable framing of
and a stable framing of 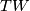 away from
away from 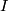 : see [Lück2001, Defintions 6.8 & 6.9] for more details.
: see [Lück2001, Defintions 6.8 & 6.9] for more details.
The set of bordism classes of closed almost framed  -manifolds forms a group under connected sum (at the unframed point) and this group is denoted
-manifolds forms a group under connected sum (at the unframed point) and this group is denoted 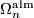 . There is an obvious forgetful homomorphism
. There is an obvious forgetful homomorphism
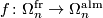
which lies in a sequence
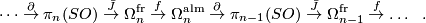
The task of this exercise is to prove that this sequence is exact: this is the statement of [Lück2001, Lemma 6.16] and may also be found in [Levine1983, Appendix (ii)]. The homomorphisms 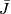 and
and 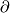 are described in [Lück2001, 6.14 & 6.15].
are described in [Lück2001, 6.14 & 6.15].
Hint: Use the J-homomorphism and the Pontrjagin-Thom construction for framed bordism as explained after the [Lück2001, Lemma 6.16] see also [Lück2001, Definition 6.23 and Lemma 6.24].
References
- [Levine1983] J. P. Levine, Lectures on groups of homotopy spheres, Algebraic and geometric topology (New Brunswick, N.J., 1983), Lecture Notes in Math., 1126 (1983), 62–95. MR802786 (87i:57031) Zbl 0576.57028
- [Lück2001] W. Lück, A basic introduction to surgery theory, 9 (2001), 1–224. Available from the author's homepage. MR1937016 (2004a:57041) Zbl 1045.57020