6-manifolds: 2-connected
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let  be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds
be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds  .
.
The classification  was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The classification, as for oriented surfaces is strikingly simple: every 2-connected 6-manifold
was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The classification, as for oriented surfaces is strikingly simple: every 2-connected 6-manifold  is diffeomorphic to a connected-sum
is diffeomorphic to a connected-sum
Tex syntax error
Tex syntax errorand in general
 is determined by the formula for the Euler characteristic of
is determined by the formula for the Euler characteristic of 
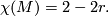
- For the more general case where
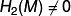 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
2 Construction and examples
The following gives a complete list of 2-connected 6-manifolds up to diffeomorphism:
-
 , the standard 6-sphere.
, the standard 6-sphere.
-
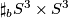 , the
, the  -fold connected sum of
-fold connected sum of 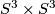 .
.
3 Invariants
Suppose that  is diffeomorphic to
is diffeomorphic to 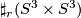 then:
then:
-
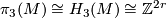 ,
,
- the third Betti-number of
 is given by
is given by 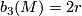 ,
,
- the Euler characteristic of
 is given by
is given by 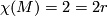 ,
,
- the intersection form of
 is isomorphic to the sum of r-copies of
is isomorphic to the sum of r-copies of  , the standard skew-symmetric hyperbolic form on
, the standard skew-symmetric hyperbolic form on 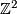 .
.
4 Classification
Recall that the following theorem was stated in other words in the introduction:
Theorem 4.1 [Smale1962a, Corolary 1.3].
The semi-group of 2-connected 6-manifolds is generated by 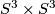 .
.
Hence if  denotes the natural numbers we obtain a bijection
denotes the natural numbers we obtain a bijection
![\displaystyle \mathcal{M}_6(0)\equiv \Nn,~~~[M] \mapsto \frac{1}{2}b_3(M).](/images/math/4/f/8/4f87caab28b3b9b7fd16a5f88c9bb677.png)
5 Further discussion
5.1 Topological 2-connected 6-manifolds
...
5.2 Mapping class groups
...
References
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103