4-manifolds in 7-space
(→The Haefliger torus) |
(→Examples) |
||
| Line 9: | Line 9: | ||
<wikitex>; | <wikitex>; | ||
| − | There is | + | There is [[Embeddings_just_below_the_stable_range#Examples#Remarks|The Hudson torus]] |
| − | [[Embeddings_just_below_the_stable_range#Examples#Remarks|The Hudson torus]] | + | |
$\Hud_{7,4,2}:S^2\times S^2\to\Rr^7$. | $\Hud_{7,4,2}:S^2\times S^2\to\Rr^7$. | ||
| − | Analogously to | + | Analogously to [[Embeddings_just_below_the_stable_range#Examples#An action of the first homology group on embeddings|the case $m=2n$]] for an orientable 4-manifold $N$, an embedding $f_0:N\to\Rr^7$ and a class $a\in H_1(N)$ one can construct an embedding $f_a:N\to\Rr^7$. However, this embedding is no longer well-defined. |
| − | [[Embeddings_just_below_the_stable_range#Examples#An action of the first | + | |
| − | homology group on embeddings|the case $m=2n$]] | + | |
| − | for an orientable 4-manifold $N$, an embedding $f_0:N\to\Rr^7$ and a class | + | |
| − | $a\in H_1(N)$ one can construct an embedding $f_a:N\to\Rr^7$. | + | |
| − | However, this embedding is no longer well-defined. | + | |
| − | We have $W_(f_u,f_0)=u$ for the Whitney invariant (which is defined | + | We have $W_(f_u,f_0)=u$ for the Whitney invariant (which is defined analogously to [[Embeddings_just_below_the_stable_range#The Whitney invariant (for either n odd or N orientable)|The Whitney invariant for $m=2n$]]. |
| − | analogously to | + | |
| − | [[Embeddings_just_below_the_stable_range#The Whitney invariant | + | |
| − | (for either n odd or N orientable)|The Whitney invariant for $m=2n$]]. | + | |
</wikitex> | </wikitex> | ||
Revision as of 12:02, 7 March 2010
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
Contents |
1 Introduction
For notation and conventions see high codimension embeddings.
2 Examples
There is The Hudson torus
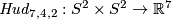 .
.
Analogously to the case 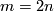 for an orientable 4-manifold
for an orientable 4-manifold  , an embedding
, an embedding 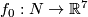 and a class
and a class 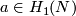 one can construct an embedding
one can construct an embedding 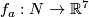 . However, this embedding is no longer well-defined.
. However, this embedding is no longer well-defined.
We have 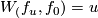 for the Whitney invariant (which is defined analogously to The Whitney invariant for
for the Whitney invariant (which is defined analogously to The Whitney invariant for 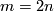 .
.
2.1 An embedding of CP2 into R7
[Boechat&Haefliger1970], p. 164.
It suffices to construct {\it an embedding 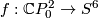 such that the
boundary 3-sphere is the standard one.}
Recall that
such that the
boundary 3-sphere is the standard one.}
Recall that 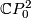 is the mapping cylinder of the Hopf map
is the mapping cylinder of the Hopf map
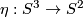 .
Recall that
.
Recall that 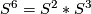 .
Define
.
Define ![f[(x,t)]:=[(x,\eta(x),t)]](/images/math/b/7/0/b7085320f1d3f79b0a9593293e4952d1.png) , where
, where 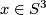 .
In other words, the segment joining
.
In other words, the segment joining 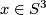 and
and 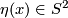 is mapped
is mapped
Tex syntax errorjoining
 to
to 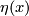 .
.
2.2 The Lambrechts torus and the Hudson torus
[Skopenkov2006].
These two embeddings 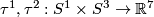 are defined as
compositions
are defined as
compositions
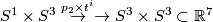 ,
where
,
where 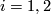 ,
,  is the projection onto the second factor,
is the projection onto the second factor,  is
the standard inclusion and maps
is
the standard inclusion and maps 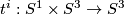 are defined below.
We shall see that
are defined below.
We shall see that 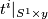 are embeddings for
each
are embeddings for
each 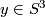 , hence
, hence 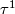 and
and 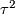 are embeddings.
are embeddings.
Define 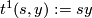 , where
, where  is identified with the set of
unit length quaternions and
is identified with the set of
unit length quaternions and 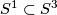 with the set of unit
length complex numbers.
with the set of unit
length complex numbers.
Define 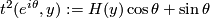 , where
, where 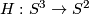 is the Hopf map and
is the Hopf map and  is identified with the 2-sphere formed by unit
length quaternions of the form
is identified with the 2-sphere formed by unit
length quaternions of the form 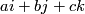 .
.
Note that 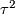 is PL isotopic to
The Hudson torus
is PL isotopic to
The Hudson torus
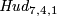 .
.
Take the Hopf fibration 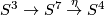 . Take the standard embeding
. Take the standard embeding 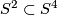 . Its complement has the homotopy type of
. Its complement has the homotopy type of  . Then
. Then 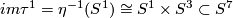 . This is the construction of Lambrechts motivated by the following property:
. This is the construction of Lambrechts motivated by the following property:
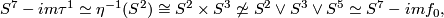
where 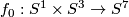 is the standard embedding.
is the standard embedding.
2.3 The Haefliger torus
This is a PL embedding 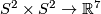 which is (locally flat but) not PL isotopic to a smooth embedding [Haefliger1962], [Boechat&Haefliger1970], p.165, [Boechat1971], 6.2. Take the Haefliger trefoil knot
which is (locally flat but) not PL isotopic to a smooth embedding [Haefliger1962], [Boechat&Haefliger1970], p.165, [Boechat1971], 6.2. Take the Haefliger trefoil knot 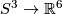 .
Extend this knot to a conical embedding
.
Extend this knot to a conical embedding 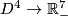 . By [Haefliger1962], the trefoil knot also extends to a smooth embedding
. By [Haefliger1962], the trefoil knot also extends to a smooth embedding
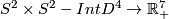 (see [Skopenkov2006], Figure 3.7.a). These two extensions together form the Haefliger torus
(see [Skopenkov2006], 3.7.b).
(see [Skopenkov2006], Figure 3.7.a). These two extensions together form the Haefliger torus
(see [Skopenkov2006], 3.7.b).
3 The Boechat-Haefliger invariant
4 Classification
5 References
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 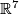 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 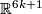 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 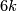 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
|
This page has not been refereed. The information given here might be incomplete or provisional. |